Deep Learning I 6~7강

길하균(Lagun)·2023년 2월 20일

Deep Learning I

목록 보기

5/6

Deep Learning I 6강 손실함수

6강에서는 딥러닝에서 쓰이는 손실함수의 개념에 대해 학습했습니다.

손실함수란?

손실함수(Loss Function)란 인공신경망을 학습시킬 때 신경망이 제대로 학습하고 있는지 판단하기 위한 지표입니다. 학습 중에 모델이 예측한 값과 실제 값 사이에 차이가 얼마나 나는지를 기준으로 판단하며 예측값과 실제값의 차이가 적어야 신경망이 제대로 학습을 하고 있다는 의미이므로 함수값이 최소가 되도록 해야합니다. 모델의 정확도를 판단하는 성능 척도와는 다른 개념임에 유의해야 합니다. 성능 척도는 모델의 학습이 끝난 후 모델의 정확도를 판단하는 척도이므로 학습 중에는 사용되지 않는 값입니다. 반면에 손실함수는 학습 중에 모델의 정확도를 판단하여 파라미터 값 조정에 반영하므로 학습 중에도 모델의 성능에 영향을 미치는 요소입니다.

손실함수는 MSE, MAE, 이항 교차 엔트로피 (Binary Cross-Entropy), 다중 클래스 교차 엔트로피 (Categorical Cross-Entropy) 등의 다양한 종류가 있지만 강의에서는 평균 제곱 오차(Mean Squared Error), 교차 엔트로피 오차(Cross Entropy Error)를 설명하고 있으므로 이번 포스팅에서도 이 둘에 대해서 정리하도록 하겠습니다.

one-hot encoding

손실함수에 대해 알아보기 전에 one-hot encoding에 대해 먼저 살펴보고 가겠습니다. 앞에서 손실함수란 인공신경망이 예측한 값과 실제값이 얼마나 차이가 나는지를 기준으로 모델이 잘 학습하고 있는지를 판단한다고 했습니다. 인공신경망의 정확도는 예측값과 실제값의 차이를 두 점 사이의 거리가 얼마나 떨어져 있는지를 기준으로 판단합니다. 다차원의 공간에서 두 점 사이의 거리를 구하기 위해서 벡터를 활용해야 하는데 이때 one-hot encoding을 이용하게 됩니다.

학습해야 하는 단어가 [사과, 포도, 오렌지, 레몬, 복숭아] 이렇게 5개 있다고 가정하겠습니다. one-hot encoding은 각 과일의 단어가 위치한 인덱스에는 1을 두고 나머지 위치에는 0을 두는 형태로 표현됩니다. 만약 '사과'를 one-hot encoding 방식으로 표현하면 [1,0,0,0,0]이 됩니다. 만약 레몬이라면 [0,0,0,1,0]이 되겠지요. 인공신경망은 입력된 데이터가 다섯 과일 중 어떤 과일인지를 확률 형태로 출력하게 됩니다. 예를 들어보자면 [0.1, 0.8, 0.05, 0.05, 0]처럼 말이죠. 이 결과의 의미는 해당 데이터가 포도일 확률이 0.8이고 사과일 확률이 0.1, 오렌지와 레몬일 확률이 0.05라는 뜻입니다. 그럼 이제 포도의 one-hot encoding인 [0,1,0,0,0]과 예측값 [0.1, 0.8, 0.05, 0.05, 0] 둘 사이의 거리를 계산하면 해당 모델의 loss 값, 즉 모델의 예측이 얼마나 맞고 틀리는지를 알 수 있게 됩니다.

평균 제곱 오차(Mean Squared Error)

평균 제곱 오차는 다차원의 공간에 신경망을 거쳐 나온 확률 벡터인 예측값과 one-hot encoding하여 나온 확률벡터인 실제값이 위치한다고 가정하고 두 점 사이의 거리를 피타고라스 정리를 이용해서 계산하는 방식입니다. 평균 제곱 오차의 식은 아래와 같습니다.

E=\frac12 \displaystyle\sum_{k}^{}{(y_k-t_k)^2}

여기서 $y_k$ 는 신경망이 $k$ 라고 예측한 확률을 의미하며 $t_k$ 는 라벨을 one-hot encoding한 $k$ 번째 좌표입니다. 이 수식을 파이썬 코드로 구현하면 아래와 같습니다.

import numpy as np

def mean_squared_error(y, t):
	return 0.5*np.sum(np.exp(x), axis=0)

교차 엔트로피 오차(Cross Entropy Error)

강의 ppt에 따르면 교차 엔트로피는 정보이론에서 확률분포사이의 거리를 재는 방법이라고 합니다. 교차 엔트로피는 정보 이론에서 두 확률 분포의 유사도를 측정하는 방법 중 하나입니다. 딥러닝에서는 데이터가 인공신경망을 거쳐서 나온 예측 확률 벡터와 one-hot encoding으로 표현된 정답 확률 벡터 사이의 차이를 측정하는 방식으로 사용됩니다. 이때 예측한 확률 분포가 실제 확률 분포와 일치할수록 교차 엔트로피 값은 작아지며, 일치하지 않을수록 값은 커집니다. 교차 엔트로피 오차의 식은 아래와 같습니다.

E = -\displaystyle\sum_{k}^{}{t_k\,log y_k}

$y_k$ 와 $t_k$ 가 의미하는 것은 평균 제곱 오차와 동일합니다. 식이 시그마로 되어 있어 모든 값을 더하는 것처럼 보이지만 one-hot encoding에서 정답이 아닌 위치의 값들은 모두 0이기 때문에 사실상 정답이 될 위치의 예측값이 얼마나 되는지만 계산하게 됩니다. 교차 엔트로피 오차를 파이썬 코드로 구현하면 아래와 같습니다.

import numpy as np

def cross_entropy_error(y, t):
	if y.ndim == 1:
    	t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    if t.size == y.size:
    	t = t.argmax(axis=1)
        
    batch_size = y.shape[0]
    return -np.sum(np.log(y(np.arange(batch_size), t))) / batch_size

Deep Learning I 7강 엔트로피

7강에서는 엔트로피의 개념과 교차 엔트로피 오차를 손실함수로 이용하는지에 대해 학습했습니다. 저에겐 아직 낯선 내용이여서 포스팅한 내용이 정확하지 않을 수 있으니 참고만 하시기를 바랍니다.

7강 엔트로피 강의 내용 요약

이번 7강은 강의 내용 요약을 먼저 보는 것이 내용을 이해하기 더 쉬울 것 같아서 강의 ppt의 마지막 페이지 내용을 우선 적어보겠습니다.

Entropy measures the uncertainty.
The reduction of entropy measures the amount of information.
Entropy is the fundamental limit for the compression of information.
Entropy measures how foa two probability distributions are to each other. This plays a key role in Machine Learning.

내용을 정리하자면 엔트로피는 불확실성을 계량화 할 수 있으며 정보의 양을 측정할 수 있습니다. 또한 엔트로피는 정보 압축의 한계점이며, 두 확률분포가 서로 얼마나 가까운지도 파악할 수 있습니다. 엔트로피를 이용하여 확률분포 사이의 거리를 측정할 수 있기 때문에 엔트로피는 머신러닝에서 중요한 역할을 합니다.

1. Entropy measures the uncertainty.

우선 엔트로피의 정의는 아래와 같습니다.

H(x)=-\displaystyle\sum_{}^{}{p(x)\, log_2\, p(x)}

정의를 이해하기 위해 강의에서는 동전던지기를 예시로 들었습니다. 이때 동전의 앞면이 나올 확률을 $p$ 라고 한다면 아래와 같이 쓸 수 있습니다.

X = \begin{cases} 1\quad with\; probability\; p,\\ 0\quad with\; probability\; 1-p \end{cases}

H(x) = -p\, log\,p \; -(1-p)\, log\,(1-p)

이때 앞면이 나올 확률인 p가 $\frac12$ 라면 $H(x)$ 는 $-\frac12log\frac12\, -(1-\frac12)log(1-\frac12) = 1$ 이 됩니다. 따라서 $p=\frac12$ 일 때 동전이 앞면이 나올 불확실성이 1로 가장 크다는 것을 알 수 있습니다. 반면에 $p$ 가 1이거나 0이 된다면 $H(x)$ 는 0이 되므로 동전이 앞면이 나오는가에 대한 불확실성은 가장 작다는 것을 알 수 있습니다.

다음으로 강의에서 사용된 두 번째 예시를 살펴보겠습니다. 두 번째 예시는 a, b, c, d 중 어떤 알파벳인지를 맞추는 문제입니다. 우선 각 알파벳이 나올 확률은 아래와 같습니다.

X = \begin{cases} a\quad with\; probability\; \frac12,\\ b\quad with\; probability\; \frac14, \\ c\quad with\; probability\; \frac18, \\ d\quad with\; probability\; \frac18 \end{cases}

이제 이 확률들을 이용해서 $H(x)$ 를 구하면 아래와 같이 $\frac74bits$ 가 나옴을 알 수 있습니다.

H(x) = -\frac12\,log\frac12\;-\frac14\,log\frac14\;-\frac18\,log\frac18\;-\frac18\,log\frac18 = \frac74bits

따라서 우리는 a, b, c, d 중 어떤 알파벳인지 맞추기 위해 $\frac74$ 만큼의 질문이 필요하다는 것을 알 수 있습니다.

다음으로는 조건부확률을 계산하는 방법을 알아보겠습니다. 두 확률변수 X와 Y가 있을 때 조건부확률 $H(Y|X)$ 를 구하는 방법은 아래와 같습니다.

\begin{aligned} H(Y|X) &= \displaystyle\sum_{}^{}{p(x)\, H(Y|X=x)}\\ &= -\displaystyle\sum_{x∈X}^{}{p(x)}\displaystyle\sum_{y∈Y}^{}{p(y|x)\,log\,p(y|x)}\\ &= -\displaystyle\sum_{x∈X}^{}\displaystyle\sum_{y∈Y}^{}{p(x,y)\,log\,p(y|x)} \end{aligned}

두 확률변수 X와 Y의 값들은 아래와 같습니다. 강의 ppt에서 캡쳐해 왔습니다.

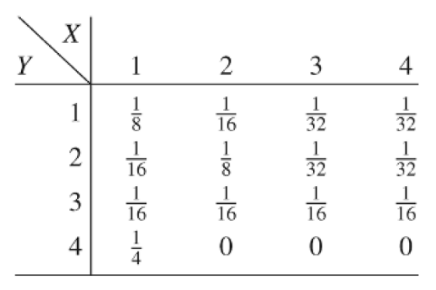
확률변수 X의 기본분포는 $(\frac12,\frac14,\frac18,\frac18)$ 이며 Y의 기본분포는 $(\frac14, \frac14, \frac14, \frac14)$ 입니다. 주어진 확률변수 X와 Y를 이용해서 $H(X|Y)$ 를 구하면 아래와 같습니다.

\begin{aligned} H(X|Y)&=\sum_{i=1}^{4}{p(Y=i)H(X|Y=i)}\\ &=\frac14H(\frac12, \frac14, \frac18, \frac18) + \frac14H(\frac14, \frac12, \frac18, \frac18) + \frac14H(\frac14, \frac14, \frac14, \frac14) + \frac14H(1, 0, 0, 0)\\ &=\frac14\times\frac74+\frac14\times\frac74+\frac14\times2+\frac14\times0\\ &=\frac{11}{8}bits \end{aligned}

따라서 Y일때 X가 발생할 확률은 $\frac{11}{8}bits$ 임을 알 수 있습니다. X일 때 Y가 발생할 확률은 $H(Y|X)=\frac{13}{8}$ 입니다. 앞서 정의한 엔트로피의 정의에 의하면 $H(x)=\frac74$ 임을 알 수 있습니다. 이제 위 식을 통해서 $H(X|Y)=\frac{11}{8}$ 임을 알았으니 이를 통해 조건부확률의 엔트로피는 X 전체의 엔트로피보다 더 낮음을 알 수 이습니다. 이 값들을 이용하면 우리는 이제 정보를 수학적으로 표현하는 것이 가능해집니다.

2. The reduction of entropy measures the amount of information.

두 번째로 살펴볼 내용은 엔트로피를 이용하여 정보를 수학적으로 정의하는 것입니다. 앞에서 구한 값들을 이용하면 두 확률변수 X와 Y가 서로의 정보를 얼마나 담고 있는지를 표현할 수 있습니다. 우선 상호정보량의 정의부터 살펴보겠습니다. 상호정보량은 아래와 같이 정의됩니다.

\begin{aligned} I(X;Y) &= \sum_{x∈X}\sum_{y∈Y}{p(x,y)\,log\frac{p(x,y)}{p(x)p(y)}}\\ &=H(X)-H(X|Y)\\ &=H(Y)-H(Y|X) \end{aligned}

위에서 정의한 수식에 앞에서 구한 값들을 넣으면 $I(X;Y)=\frac38$ 임을 알 수 있습니다. 이 값은 곧 확률변수 Y가 확률변수 X에 대해 가지고 있는 정보량을 의미합니다. 만약 확률변수 X와 Y가 서로 독립이라면 $H(X|Y)$ 를 알아도 쓸모가 없으므로 X와 Y사이의 정보량은 0이 됩니다. 즉 두 확률변수는 서로 아무런 정보도 가지고 있지 않습니다.

3. Entropy is the fundamental limit for the compression of information.

어떤 단어를 코드로 만든다고 할 때 가능하면 코드의 길이가 짧은 것이 좋습니다. 하지만 그렇다고 무조건 짧은 코드를 쓴다면 단어를 구별할 수 없는 문제가 발생할 수 있습니다. 이때 엔트로피를 이용하면 정보를 어디까지 압축할 수 있는지를 파악할 수 있습니다. 압축의 한계값을 구하는 식은 아래와 같습니다.

L(C) = \sum_{x∈X}{p(x)l(x)}

이때 $p(x)$ 는 보내려는 글자에서 단어가 등장할 확률이며 $l(x)$ 는 보내고 싶은 단어 코드의 길이입니다. 1, 2, 3, 4를 코드로 바꿔 보내려고 한다고 가정할 때 각 숫자의 등장빈도와 코드는 아래와 같습니다.

\begin{aligned} Pr(X=1)&=\frac12,\quad codeword\; C(1)=0\\ Pr(X=2)&=\frac14,\quad codeword\; C(2)=10\\ Pr(X=3)&=\frac18,\quad codeword\; C(3)=110\\ Pr(X=4)&=\frac18,\quad codeword\; C(4)=111 \end{aligned}

따라서 예상되는 단어 코드의 길이는 $L(C)=\frac12\times1+\frac14\times2+\frac18\times3+\frac18\times3=\frac74$ 임을 알 수 있습니다. [1, 2, 3, 4]를 이진수로 표현하면 [00, 01, 10, 11]과 같이 표현할 수도 있지만 등장빈도를 고려했을 때 위와 같이 [0, 10, 110, 111]로 표현하는 것이 더 효율적임을 알 수 있습니다.

4. Entropy measures how foa two probability distributions are to each other.

이제 엔트로피가 머신러닝에서 어떻게 활용될 수 있는지를 살펴보겠습니다. 엔트로피를 이용해서 머신러닝이 잘 학습하고 있는지를 판단하려면 상대 엔트로피를 알아야 합니다. 상대 엔트로피는 두 확률분포의 차이를 계산하는 식으로 아래와 같습니다.

D(p||q)=\sum_{x∈X}{p(x)\,log\frac{p(x)}{q(x)}}

위에서 엔트로피 $H(X)$ 의 정의는 $H(x)=-\displaystyle\sum_{}^{}{p(x)\, log\, p(x)}$ 라고 하였고, $H(p,q)=-\displaystyle\sum_{}^{}{p(x)\, log\, q(x)}$ 이므로 위 식은 아래와 같이 간단하게 정리할 수 있습니다.

\begin{aligned} D(p||q)&=-\sum_{x∈X}{p(x)\,log\,{q(x)}}+\sum_{x∈X}{p(x)\,log\,{p(x)}}\\ &= H(p,q)-H(p) \end{aligned}

이때 $p$ 를 라벨 $k$ 의 ont-hot 벡터 t=(0, $\cdots$ ,0,1,0, $\cdots$ ,0)으로 잡고 $q$ 를 신경망이 예측한 확률 벡터인 ( $y_0$ , $y_1$ , $\cdots$ , $y_9$ )로 잡으면 $H(p)=0$ 이므로 결국은 위 식에서 $H(p,q)$ 만 남게 됩니다. 이 $H(p,q)$ 를 이용해서 두 확률분포 사이의 거리를 표현할 수 있으며 이를 교차 엔트로피라고 부릅니다. 따라서 6강의 교차엔트로피 오차가 $E = -\displaystyle\sum_{k}^{}{t_k\,log y_k}$ 와 같이 나오게 된다는 것을 알 수 있습니다.