Deep Learning I 8강

Deep Learning I 8강 수치미분과 gradient

8강에서는 수치미분과 gradient의 개념에 대해 학습했습니다.

수치미분

인공신경망에서 수치미분이 필요한 이유는 뭘까요? 전부터 딥러닝에서 미분을 이용하는 이유를 확실하게 이해하지 못했었는데 이번 강의를 통해 궁금증을 해소할 수 있었습니다. 딥러닝에서 미분을 이용하는 이유는 간단히 말해서 정답이 위치한 방향으로 학습하기 위함입니다. 앞선 강의에서 인공신경망이 맞춰야 하는 정답들은 one-hot encoding을 통해 벡터 형태로 표현된다고 배웠습니다. 따라서 정답들을 좌표 위의 점으로 표현할 수 있게 되고 이를 통해 정답과 예측값 사이의 차이도 계산할 수 있었습니다. 여기서 아이디어를 확장해보면 두 점 사이의 기울기를 이용하여 어느 방향으로 가중치와 편향을 바꿔야 정답에 더 가까워 질 수 있는지를 판단할 수 있다는 아이디어에 도달하게 됩니다.

이때 우리가 고등학교 수학에서 배운 미분의 정의를 이용하여 구한 미분계수를 이용하는 것이 가장 좋겠지만 컴퓨터는 이 미분을 정확히 계산하지 못하여 중앙차분 오차가 발생하기 때문에 수치미분을 이용해야 합니다. 이때 미분의 정의에서의 $h$는 충분히 작은 값(강의에서는 $10^{-4}$를 예시로 들었습니다.)을 넣어줍니다. 다만 이때 너무 작은 $h$는 넣지 않는 것이 좋습니다. 그 이유는 1bit에 담을 수 있는 정보가 한정되어 있기 때문에 너무 작은 값을 넣으면 $h$가 0이 될 수 있기 때문입니다.

수치미분에는 아래와 같이 전방 차분법과 중앙 차분법이 있습니다. 전방 차분법을 이용하는 것보다 중앙 차분법을 이용하는 것이 실제 미분값에 더 가깝기 때문에 딥러닝에서는 중앙 차분법을 이용합니다.

코드로 구현한 수치미분

위에서 살펴본 수치미분을 python 코드로 구현하면 아래와 같습니다.

def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

gradient

인공신경망에서 사용할 함수는 일변수 함수가 아닌 다변수 함수입니다. 위에서 인공신경망을 학습시키기 위해서는 미분을 이용한다고 하였습니다. 따라서 편미분의 개념에 대해 알고 있어야 합니다. 다만 제 포스팅은 강의를 하기 위함이 아니라 강의를 하며 배운 내용을 정리하는 용도이기 때문에 편미분에 대해서는 다루지 않겠습니다.

인공신경망에서 사용하는 다변수 함수의 편미분을 python의 for문을 이용해서 위의 numerical_diff와 같이 일일이 계산한다면 연산 시간이 엄청나게 증가할 것입니다. 따라서 딥러닝에서는 gradient vector를 이용해서 기울기를 효율적으로 연산합니다. 각 변수에 대한 편미분을 벡터로 모아둔 것을 기울기 벡터(gradient vector)라고 합니다.

이때 방향 미분이 가장 커지는 방향은 gradient 방향이며 그 값은 gradient의 크기입니다. 반대로 방향 미분이 가장 작아지는 방향은 gradient의 반대 방향이며 값은 gradient의 마이너스의 크기입니다. gradient의 수직인 방향은 방향 미분이 0이 됩니다. 이를 통해 등고선을 그릴 수 있고, 정답에 도달하는 가장 빠른 방향을 구할 수 있습니다.

코드로 구현한 gradient

이제 코드로 구현한 gradient를 살펴보도록 하겠습니다. 코드는 강의에서 사용한 코드를 가져온 것입니다.

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

# 그래디언트를 구해주는 함수
def _numerical_gradient_no_batch(f, x):
    h = 1e-4 
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        
        # f(x+h) 계산
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)
        
        # f(x-h) 계산
        x[idx] = tmp_val - h 
        fxh2 = f(x)
        
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val  # 값 복원
        
    return grad

def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad

def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)

def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()

    grad = numerical_gradient(function_2, np.array([X, Y]).T).T

    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.draw()
    plt.show()

코드에 대해서 간단히 설명해보자면 앞서 얘기한 벡터들을 표현한 벡터장을 출력하는 코드입니다. 코드에서 h를 1e-4로 잡은 이유는 위에서 언급한대로 수가 너무 작으면 1bit에 저장 가능한 용량을 넘어서 $h$ 값이 0이 될 수 있기 때문입니다. 코드를 실행하면 아래와 같은 그래프가 나옵니다.

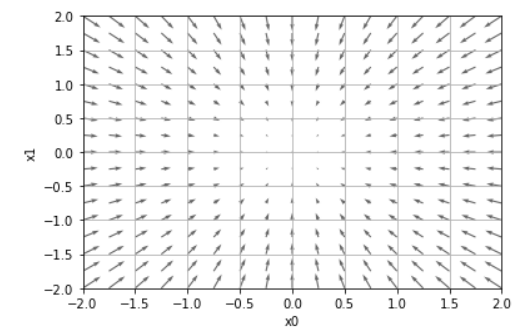
코드 실행 결과 벡터장의 화살표들이 원점을 향하고 있는 것을 확인할 수 있습니다.