ESPREOMEDIA MODEL STUDY
1. Introduction to Deep Learning
What you'll learn
- Basic of NN and Deep learning: 어떻게 데이터를 가지고 학습을 하는지, 어떻게 Neural Network를 설계하는지 등을 배워 최종적으로 고양이 인식기를 만들게 될 것이다.
- Improving Deep Learning Network: NN이 어떻게 작동하는지, hyperparameter는 어떻게 tuning하는지, bias와 variance는 어떻게 분석하는지, Optimization과 Regularization의 방법은 어떤 것들이 있는지를 배우게 된다.
- Structuring Machine Learning Project: ML 프로젝트를 어떻게 설계하는지 배울 예정이다. (ex,Train Dataset, Test Dataset 구성 등에 대해)
- CNN: 주로 이미지에 적용되는 CNN 구축 방법에 대해 배운다.
- Natural Language Processing: 자연어 처리 및 시퀀스 모델에 대해 배우게 될 것
2. What is NN ?
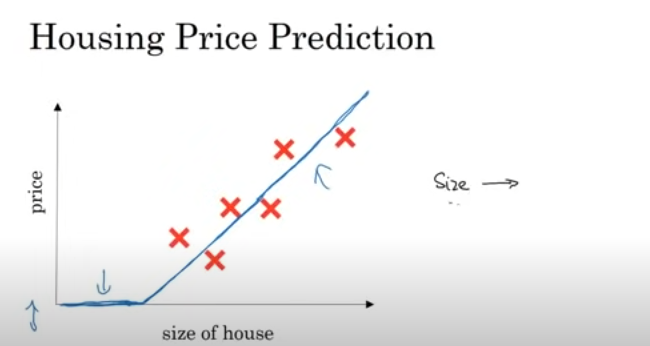
Housing Price Prediction
size (x) -> f(x) -> price (y)
여기서의 f(x)를 neuron이라고 보며, 뉴런이 하는 일은 주택의 크기를 입력으로 받아서 선형 함수를 계산하고, 결과값과 0중 큰 값을 집값으로 예측을 하는 것입니다.
즉 신경망이란 ! 입력(x)와 출력(y)를 매칭해주는 함수를 찾는 과정입니다.
=> 0으로 유지되다 직선으로 올라가는 형식의 함수를 자주 보게 된다. (ReLU)
이것은 Single Neuron의 경우가 된 상태이고, 이런 Neuron을 레고라고 생각하게 되면 DNN의 경우는 여러개의 레고가 쌓인 케이스라고 보면 된다.
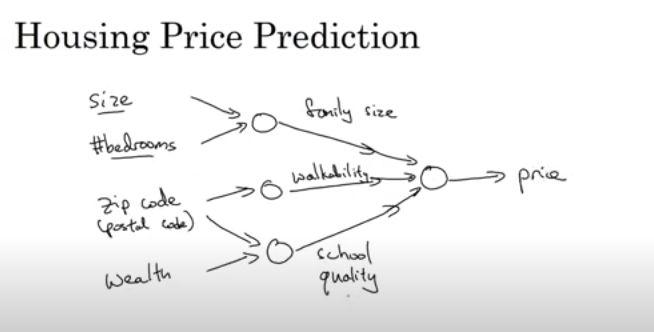
집 값 예측 모델을 예로 들면 실제로는 집의 크기만이 집의 가격에 영향을 끼치는 것이 아니기에 다양한 파라미터들이 존재한다. 이 설명은 하단의 그림을 참조하면 된다.
여기서 충분한 양의 x(변수 likes size, bedrooms, zip code, wealth in house price prediction)과 y(변수 likes price in house price prediction)가 주어진다면 NN은 x를 y로 연결해주는 함수를 알아내는데 도움이 된다.
3. Supervised Learning with Neural Networks
in supervised learning
input(x)와 output(y)에 대해 매핑되는 함수를 학습하려고 한다.
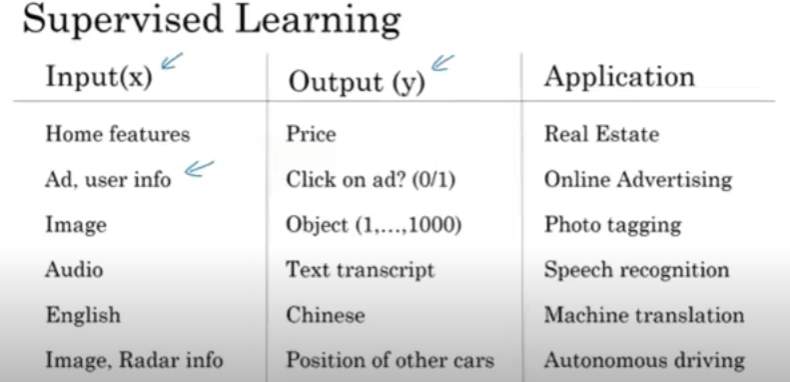
Supervised Learning의 종류는 다음과 같다.
여기서 집값 예측, 온라인 광고 관련된 모델은 Standard NN이 사용되며, Image에 관련된 모델은 CNN 기반의 모델이 사용되고, 음성 혹은 언어같은 시퀀스 데이터같은 경우엔 RNN을 사용한다.
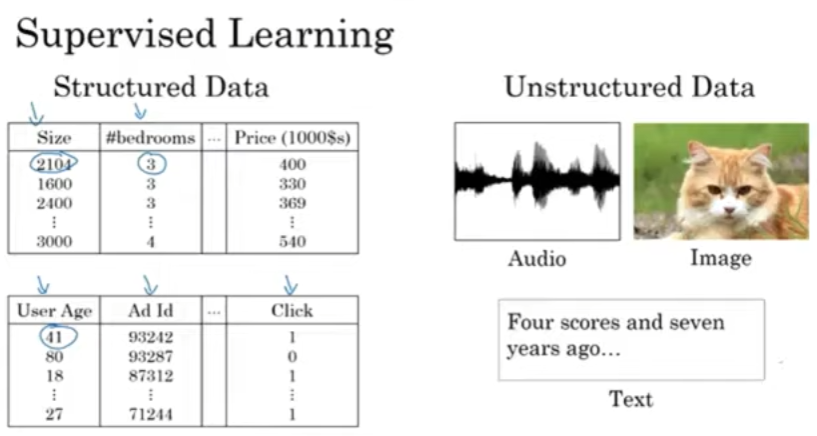
머신러닝분야에서 구조적 데이터 / 비구조적 데이터를 사용하여 신경망을 사용하여 예측할 수 있다.
구조적 데이터 : Database로 표현된 데이터를 말합니다. 정보의 특성이 잘 정의되어있는 것을 말한다.
비구조적 데이터 : 이미지, 오디오, 텍스트와 같은 형태의 데이터이다. 니는 특정적인 값을 추출하기가 어려운 형태의 데이터이고, 딥러닝 덕분에 컴퓨터가 비구조적 데이터를 인식할 수 있게 되었다.
4. Why is deep learning taking off
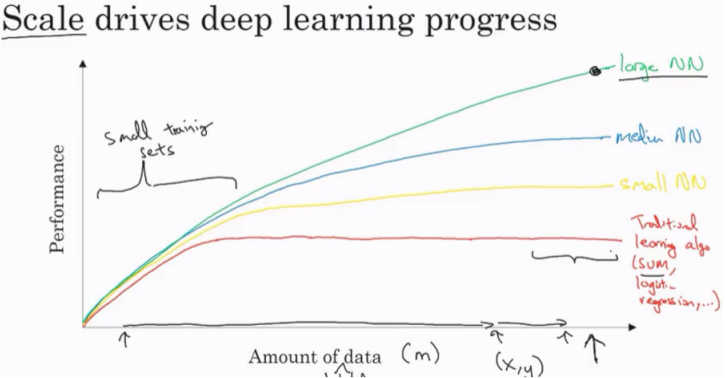
기존의 알고리즘은 데이터 양이 증가함에 따라 성능이 좋아지긴 하지만 일정 구간을 지나면 정체기가 오게 된다.
하지만, small NN~large NN은 훈련시키게 된다면 성능은 계속해서 좋아지게 됩니다.
-> 그래서 규모가 신경망의 발전을 가져왔다고도 한다.
사실 오늘날 성능을 올릴 때 가장 신뢰할 수 있는 방법은 더 큰 신경망을 훈련시키거나 더 많은 데이터를 집어넣게 되는 것인데 이는 한계가 있다.
But 단순히 규모를 키우는 것만으로도 성능이 올라가게 되었다.
최근 딥러닝이 강력한 도구로 부상한 이유는 하단의 3가지 요인들로 인해 딥러닝 성능이 향상되었다.
1. 데이터 양의 증가
2. 컴퓨터 성능 향상
3. 알고리즘 개선
==> ex) sigmoid 함수가 아닌 Relu를 사용함으로써 Gradient 소멸 문제를 해결했다. 이유 : sigmoid때는 함수의 경사가 거의 0인 곳에서 학습이 굉장히 느려진다.[경사가 0일 때 경사하강법을 사용하면 파라미터가 천천히 바뀌고 학습이 느려지기 때문] 반대로 ReLU의 경우는 입력값이 양수인 경우 경사가 1로 모두 같으므로 경사가 서서히 0에 수렴할 경우가 적기 때문이다.
5. Binary Classification
이진 분류란 True or False의 2개로 분류를 하는 것인데, 이때 결과가 Ture면 1, False면 0으로 표현하게 된다.
(ex. 고양이다 or 고양이가 아니다)
또한 이진 분류의 목표는 입력된 사진을 나타내는 feature vector "x"를 가지고 그에 대한 lable "y"가 1 아니면 0으로 예측할 수 있는 분류기를 학습하는 것이다.
6. Logistic Regression
로지스틱 회귀는 이진 분류 Task에서 사용하게 된다.
이때 x는 입력 특성, y는 주어진 입력 특성 x에 해당하는 실제 값, y'은 y의 예측값을 의미한다.
여기서 y'의 크기는 1과 0사이의 값이어야한다.
로지스틱 회귀에서는 시그모이드 함수를 적용하여 출력된 값을 내게 되는데 이때 값은 0과 1사이의 값으로 출력되게 됩니다.
7. Logistic Regression cost function
우리의 목표는 실제값(y)에 가까운 예측값(y')을 구하는 것이다.
보통의 손실함수는 L(y',y) = 1/2(y'-y)^2를 사용하지만, 로지스틱 회귀에서 이러한 손실함수를 사용하면 local minimum에 빠질 수 있기 때문에 사용하지 않는다.
따라서 Loss function을 다르게 정의하여 사용되는데, 이때 사용되는 수식이
L(y',y) = - (y*log(y') + (1-y)*log(1-y'))=> 만약 square root error를 사용하게 된다면 이 error를 최소화하려고 할 것이다. 이와 같이 Logistic Regression Loss Function 을 사용할 때 이 값을 최소화해야한다.
왜 이 함수를 사용해야하는가?
1. y가 1일 경우 : loss function "l"은 그냥 -log(y')이 된다. 이때 -log(y') 이 최대한 커지기를 원할 것이다. [왜냐하면 y=1 즉 참이고, y'도 1에 가까운 값이 나와야하기 떄문에] 그러려면 log(y')값이 최대한 커져야하며 따라서 y'이 최대한 커야한다. But y'은 sigmoid 함수 값이기 때문에 1보다 클 수 없다.
- y가 0일 경우 : Loss function은 -log(1-y')이다. -때문에 log(1-y')이 최대한 커야한다.
Cost Function(=Loss Function)은 훈련 세트 전체에 대해 얼마나 잘 추측되었는지 측정해주는 함수다.
8. Gradient Descent
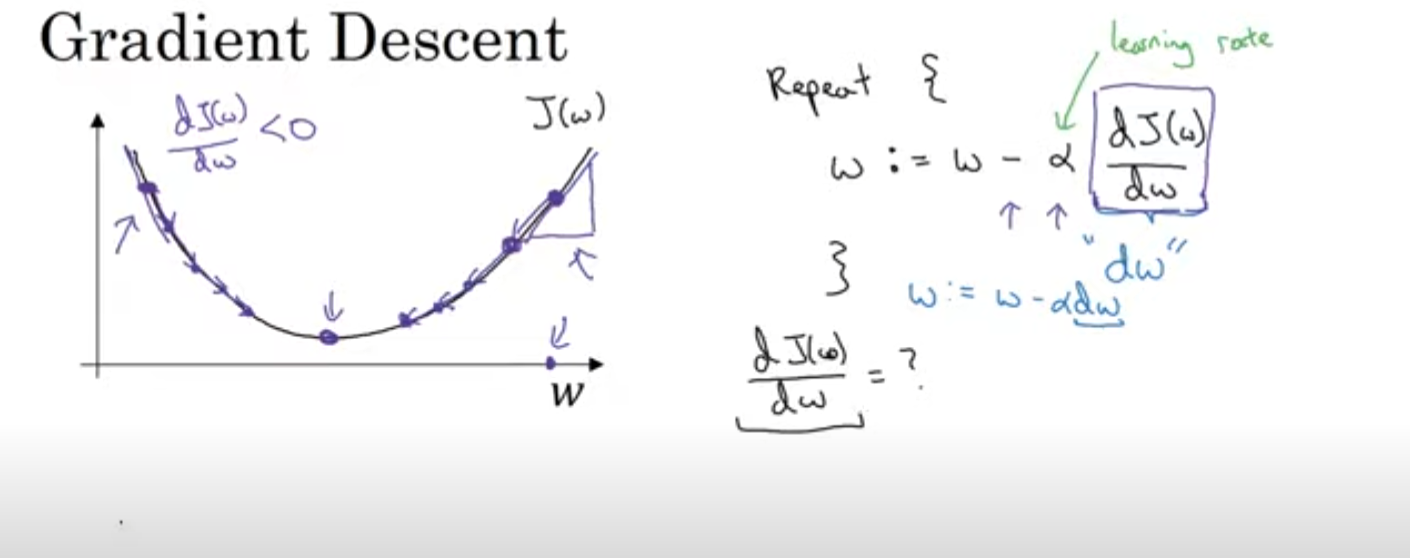
특정 비용함수 J가 만약 볼록하지 않은 함수가 있다면 이것은 Local minimum이 여러개이지만, 현재 그래프에서 가장 값을 작게 만드는 w,b의 값을 찾는 것이 목표이다.
경사하강법은 가장 가파른 방향, 즉 함수의 기울기를 따라서 최적의 값으로 한 스텝씩 업데이트하게 되는데, 알고리즘은 다음과 같다.
9. Derivatives
이 Derivatives는 미분을 뜻하며 한 함수에서의 미분 값은 기울기라고 볼 수 있다.
예를 들어 linear line의 모양을 한 함수에서 a=2가 있다면 f(a) = 3a 라는 식에서 f(a)의 값은 6이다. 만약 a에 0.001만큼 이동을 한다면 f(a) = 0.0013만큼 이동한 값이 나온다. 가로축에서 0.001만큼의 증가가 세로축의 0.003만큼의 이동이 생겨 이 기울기(미분값)은 3이라고 말한다.
10. Computation graph
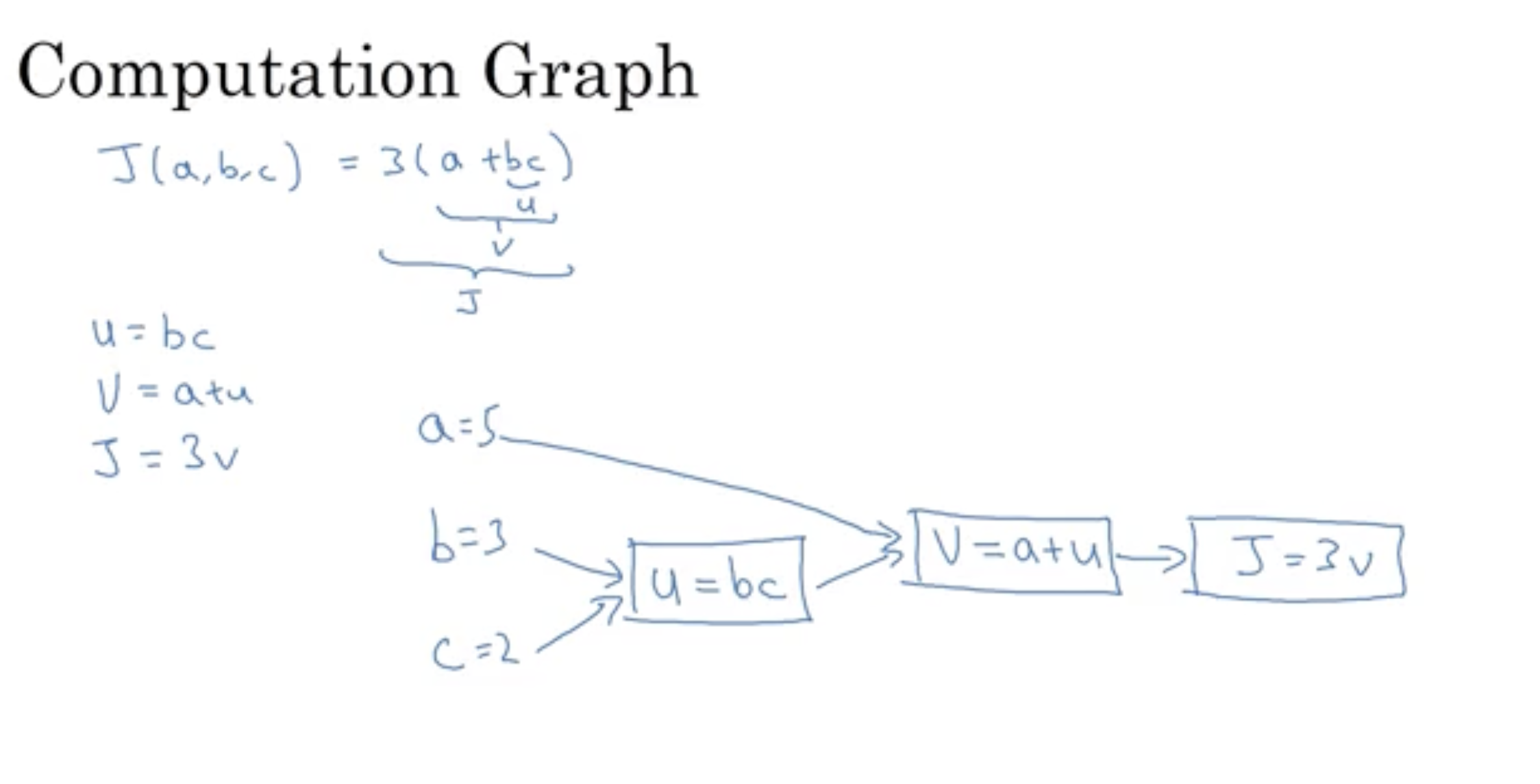
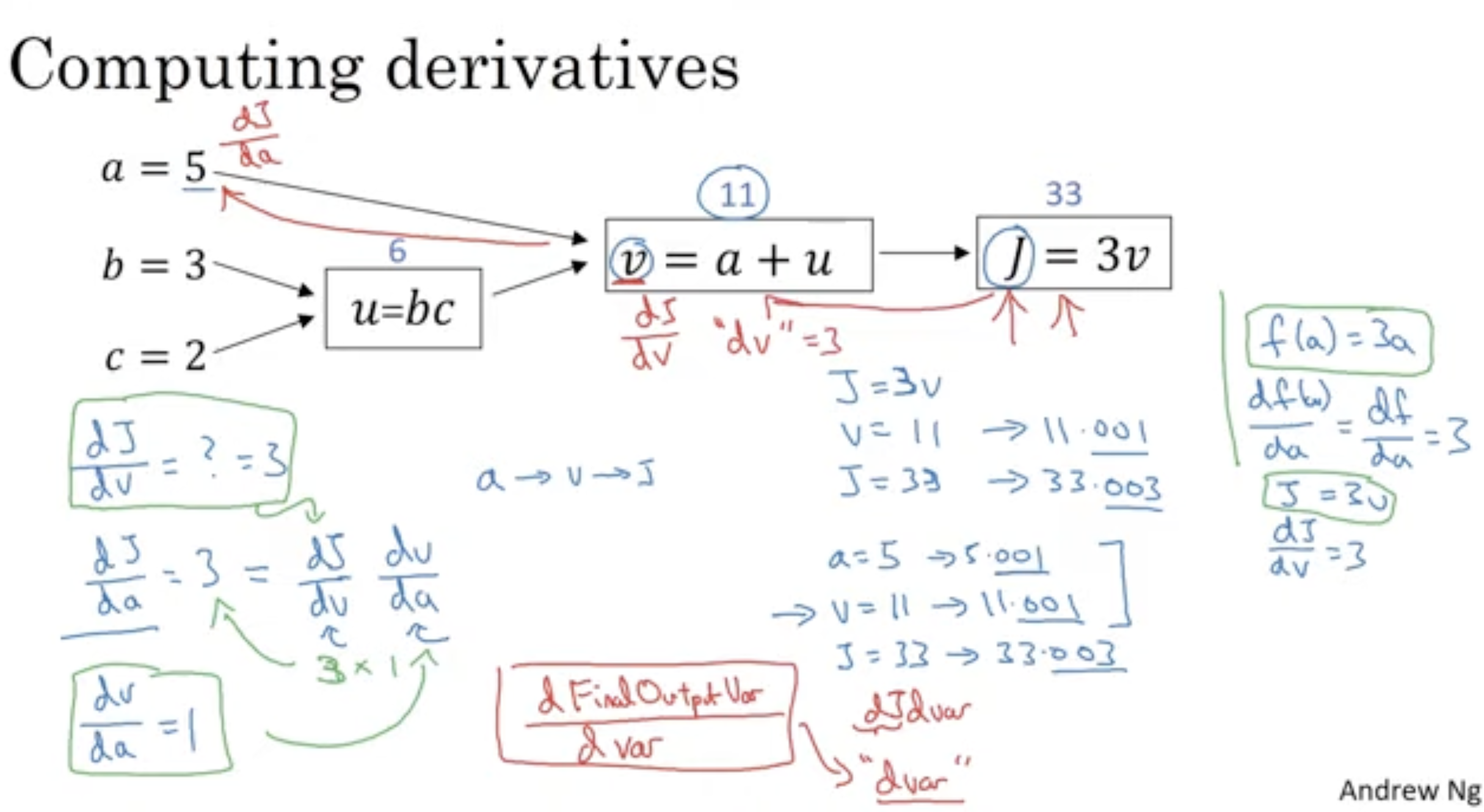
J(a, b, c) = 3(a+bc)에 대한 계산 그래프를 그리는 방법은 상단의 그림과 같다.
상단의 수식에 대한 도함수를 구하기 위해 오른쪽에서 왼쪽으로 가는 것에 대한 학습이 추가될 예정이다.
11. Derivatives with Computation Graph
미분의 연쇄법칙이란 합성합수의 도함수에 대한 공식이다. 합성함수의 도함수는 합성함수를 구성하는 함수의 미분을 곱함으로써 구할 수 있다.
-> 입력변수 a를 통해서 출력변수 j에 도달하기 위해 a -> v -> j의 프로세스를 진행한다.
이런 함수에서 a의 일정양을 j에 밀게 되었을 때의 값은 a의 일정양을 v에 밀게 되었을 때의 값과 v의 일정양을 j에 밀게 되었을 때의 값의 곱과 동일하다.
v에 대한 dJ의 도함수도, a에 대한 dJ의 도함수도 3이 나온다. 구하는 방법은 다음 그림과 같다
12. Logistic Regression Gradient Descent
==> 이 부분은 이해하지 못해, 이해 후 변경될 부분이다.

13. Gradient Descent on m Examples

J, dw1, dw2, db = 0이라고 전부 초기화를 진행
logistic regression에서 loss function을 구하는 것을 다음과 같이 코드로 구현할 수 있다. 이 코드에서 이중 for 문을 사용하게 되는데 이로 인해 계산 속도가 느려지게 된다.
현재 코드에서는 특성(dw)의 개수를 2개로 가정했지만, 만약 특성의 개수가 많아진다면 for문을 사용해 처리해야한다.
이러한 for문의 문제를 제거하기 위해 vectorization을 활용한다.
14. Vectorization
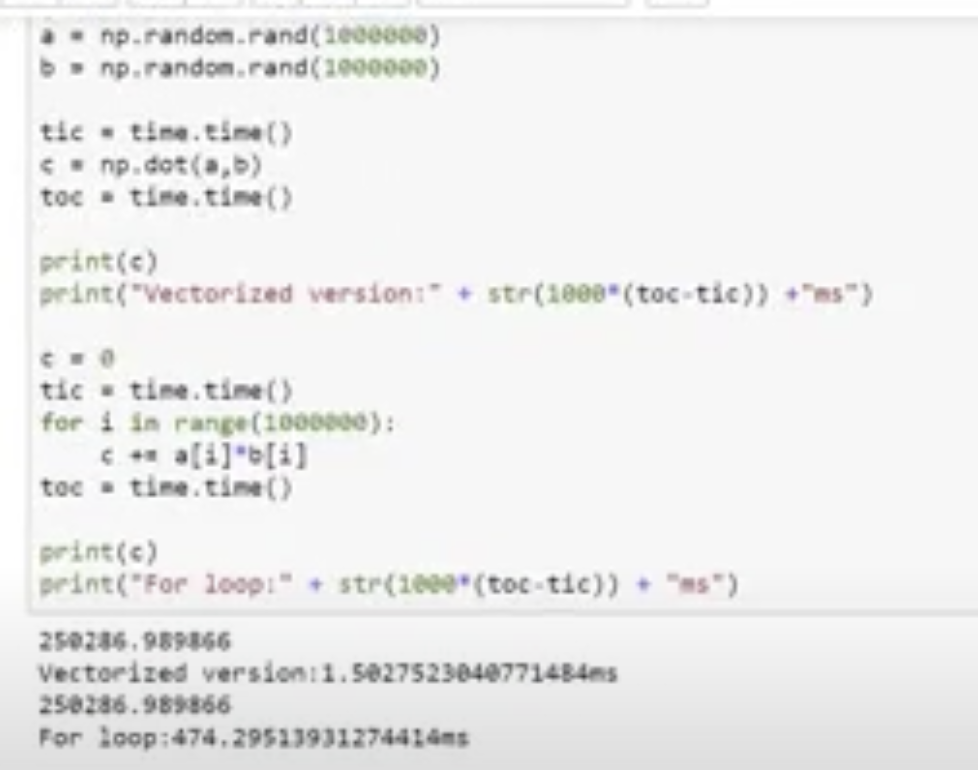
벡터화는 for문을 사용하여 연산할 때 오래 걸리는 것을 방지하기 위해 사용되며, python or numpy에서 np.dot(w,x)로 간단하게 y = w^t * x + b를 연산할 수 있다.
걸리는 시간의 차이는 하단의 사진을 보면 된다.
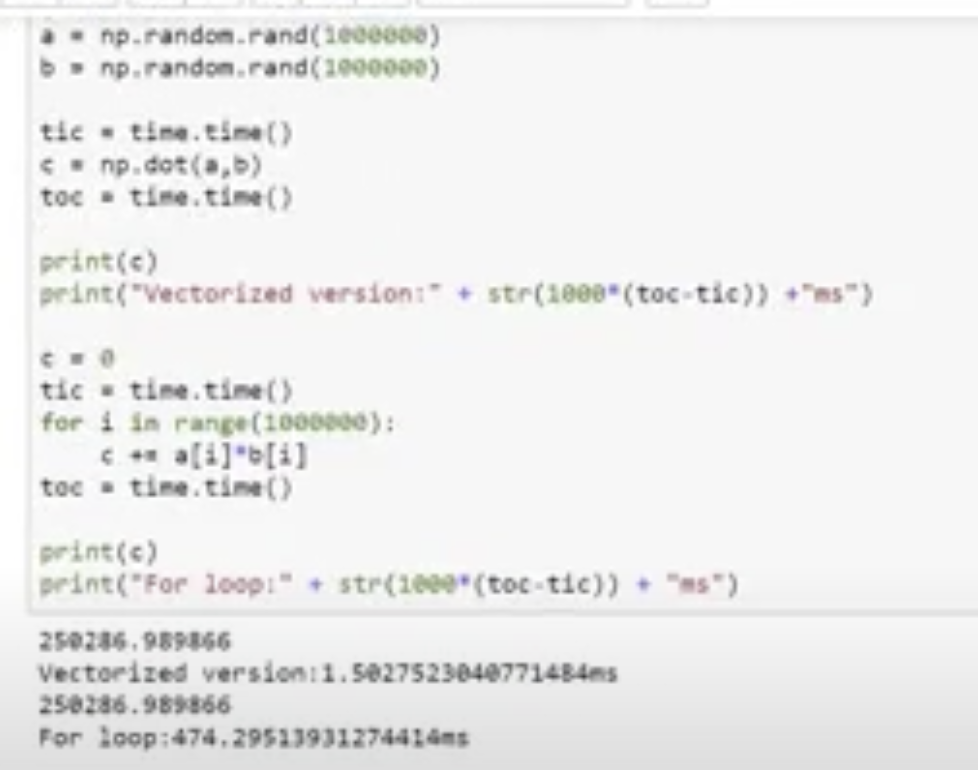
GPU와 CPU에는 SIMD(Single Instruction Multiple Data)라는 병렬 명령어가 있는데, 이는 하나의 명령어로 여러 개의 값을 동시에 계산하는 방식이다. 이는 벡터화 연산을 가능하게 합니다.
15. More Vectorization Examples
컴퓨터의 계산 효율성을 위해 가능한 for 문을 사용하지 않는 것이 좋다.
자주 쓰는 np function에는 log, abs, maximum, ** zeros 등이 있다.
16. Vectorizing Logistic Regression
사진의 계산처럼 z와 a에 대한 값을 구해야하는데, 계산의 효율성을 증가시키기 위해 벡터를 이용하면,
Z = np.dot(np.transpose(W),X) + b 로 표현이 가능하다.
위의 코드에서 (1, m) 크기의 행렬과 상수 b를 더할 때, 파이썬이 자동적으로 상수를 (1,m)의 크기의 행렬로 broadcasting 해주어 오류가 발생하지 않는다.
17. Vectorizing Logistic Regression's Gradient Computation
Logistic Regression Gradient Descent 강의에서 dz = a(i) - y(i)를 통해 계산할 수 있다는 것을 확인했다.
for 문을 사용하여 계산한다면 다음과 같지만

이를 벡터화하여 계산 속도를 더 빠르게 한다면

18. Explanation of Logistic Regression's Cost Function
노트 필기 참조해서 다시 채워 넣을 것
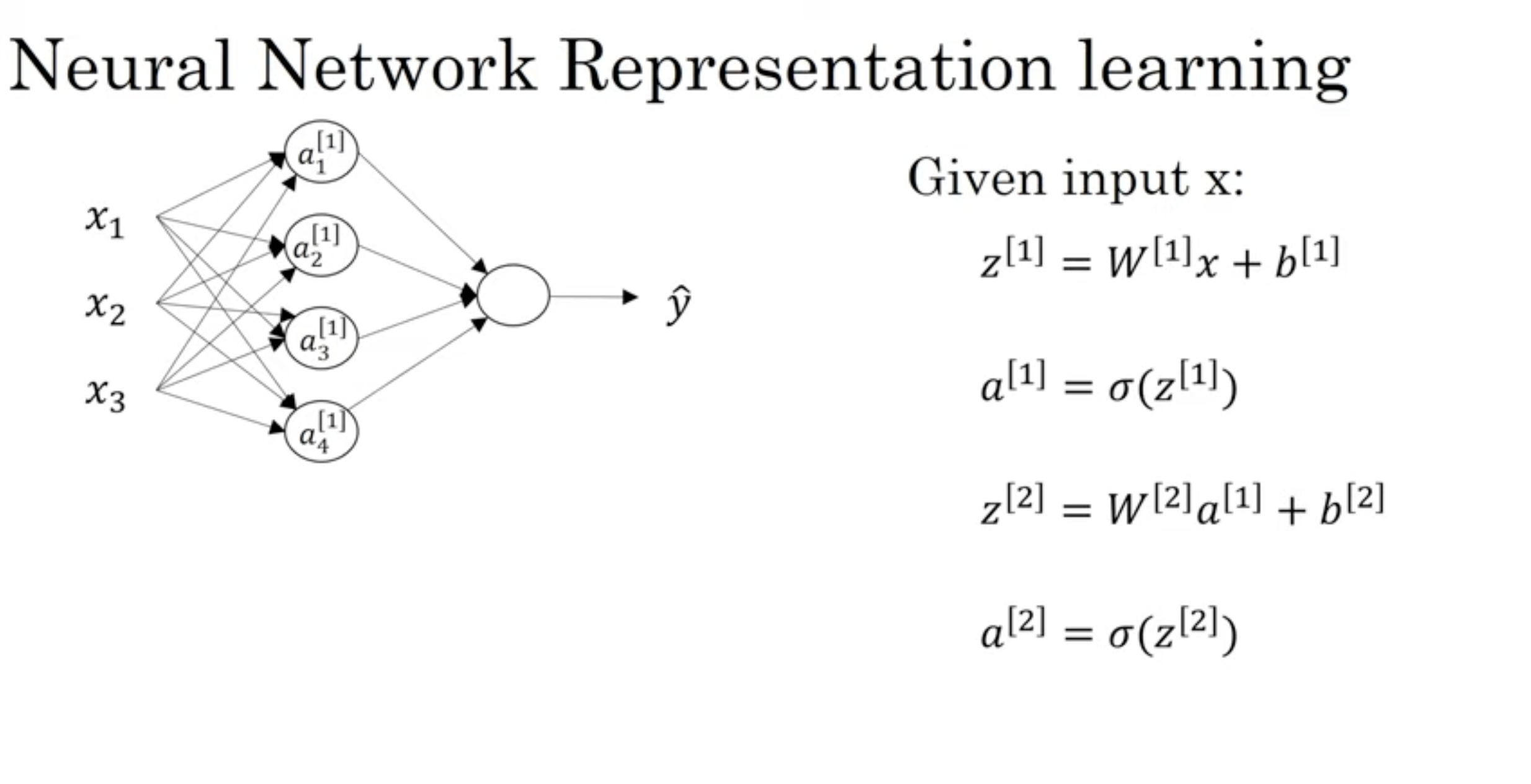
19. Neural Network Representation
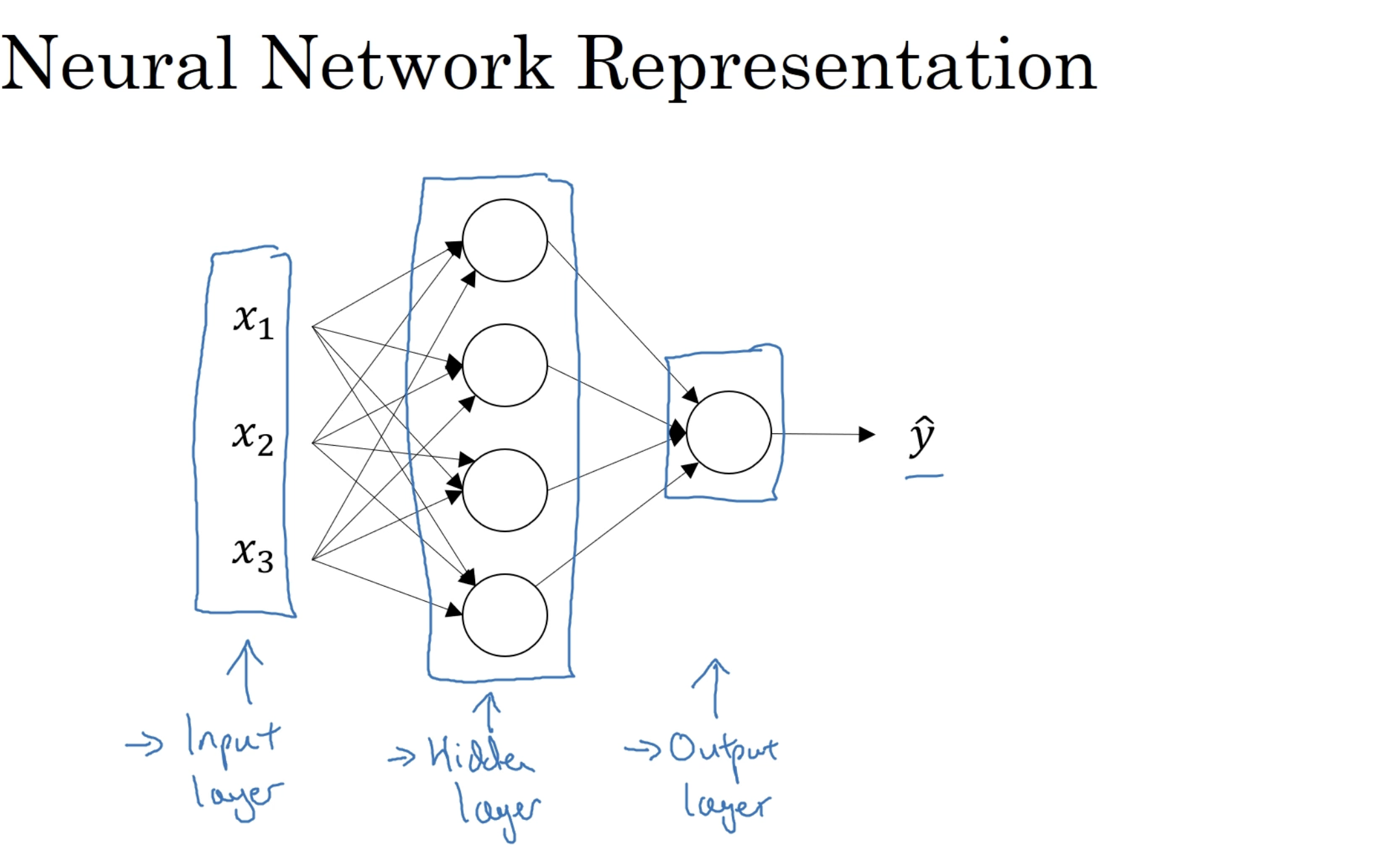
상단의 그림은 은닉층 1개, 출력층 1개이기에 2층 신경망이라고 불리며 (입력층은 관례적으로 세지 않는다)
입력값의 다른 표기법은 a[0] (입력층의 활성화 값)이다.
a는 활성화값을 말하며 신경망의 층들이 다음 층으로 전달해주는 값을 의미한다.
입력층은 x를 은닉층으로 전달해준다.
20.Computing Neural Network Output
입력값이 노드를 통과할 때, 두가지 과정을 거치게 된다.
1. z=w^T + b
2. a = σ(z)
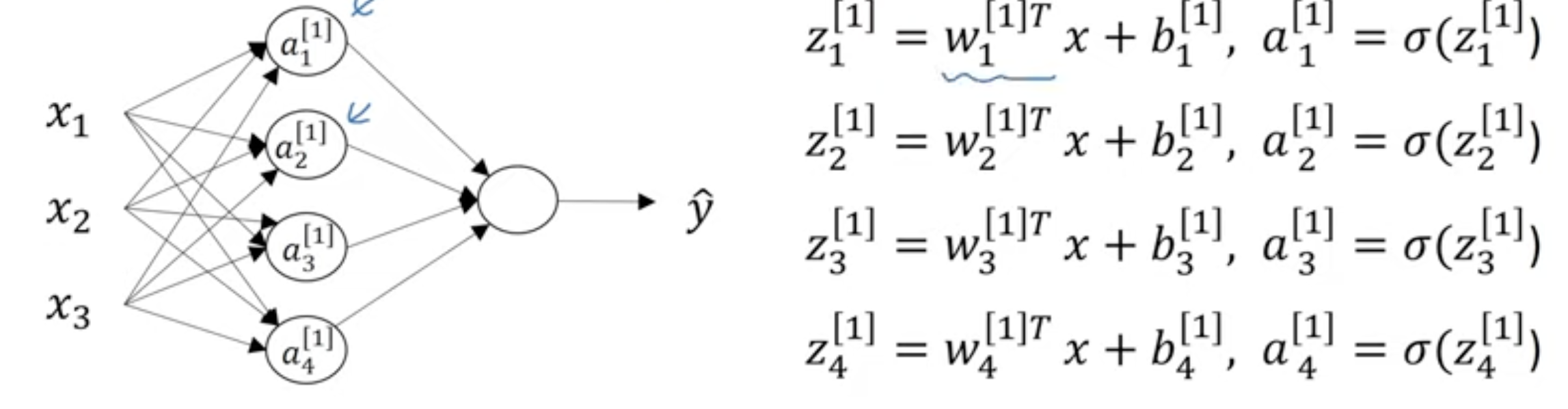
다음의 그림에서 노드 내 쓰여있는 a에 대한 표기법 중,
l은 몇 번째 layer인가에 대한 표기고, i는 해당 layer에서 몇번째 노드인지를 의미한다.
x가 주어졌을 때의 결과 값은 다음과 같다.