퀵정렬
퀵정렬은 분할 정복 알고리즘의 하나로,
중복된 값을 입력 순서와 상관없이 무작위로 뒤섞인 상태에서 정렬이 이루어지는 불안정 정렬이며 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬이다
분할 정복 알고리즘?
분할 정복 알고리즘은 말 그대롭 분할하고 정복하는 것이다.
분할: 하나의 문제를 더이상 분할 할 수 없는 동일한 유형의 여러 하위 문제로 나눈다.
정복: 가장 작은 단위의 하위 문제를 해결하여 정복
조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
퀵정렬 알고리즘에서 어떻게 분할 정복을 하는지에 대해서 알아보자.
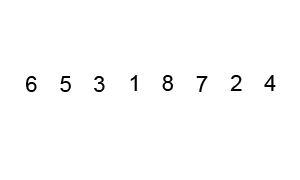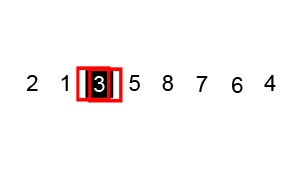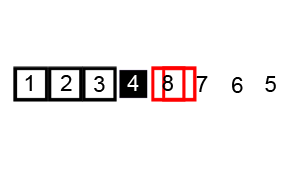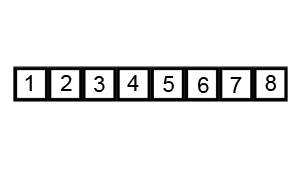
먼저 검은색 상자(피벗)을 중앙에 있는 값으로 설정하고 이걸 기준으로써 정렬을 시작한다.
기준이 된 검은색 상자의 왼쪽과 오른쪽의 끝부터 하나하나씩 피벗값과 비교하면서
왼쪽(left): 피벗값보다 큰 값이 올 경우 정지.
오른쪽(right): 피벗값보다 작은 값이 올 경우 정지.
이렇게 찾은 값들을
[col[left] , col[right] ] = [col[right] , col[left] ] 로 교환한다.
만약 left right 둘다 못 찾았고 피벗 값으로 왔을 경우에 해당 피벗 값을 방문했음을 확인한 후, 다음 피벗 값을 정하여 다시 정렬한다.
function quickSort(array, left = 0, right = array.length - 1) {
if (left >= right) return;
let l = left;
let r = right;
let pivot = array[Math.floor((left + right) / 2)];
while (l <= r) {
// 양쪽에서 각자 값을 찾고
while (array[l] < pivot) l++;
while (array[r] > pivot) r--;
// 값이 있을 경우에만
if (l <= r) {
[array[l], array[r]] = [array[r], array[l]]; // 각 값을 스왑
l++;
r--;
}
}
if (l < right) {
quickSort(array, l, right);
}
if (r > left) {
quickSort(array, left, r);
}
return array;
}
console.log(quickSort([9, 4, 6, 2, 8, 1, 3]));
재귀
재귀란 함수에서 자기 자신(함수)를 다시 호출하는 것이다.
재귀에서 대표적으로 예시를 들 수 있는 것은 팩토리얼이다.
function factorial(n) {
if (n === 1) {
return 1;
}
return n * factorial(n - 1);
}
const save = factorial(sampleNumber);
console.log(save);이렇게 재귀함수를 이용하여 팩토리얼을 쉽게 구할 수 있다.
해시테이블
(key,value)로 데이터를 저장하는 자료구조로써
하나의 데이터를 빠르게 검색할 수 있는 자료구조이다.
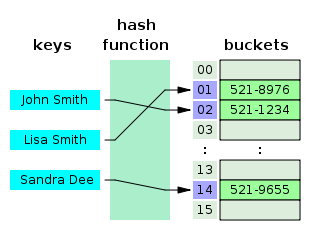
테이블이 빠른 검색속도를 제공하는 이유는 내부적으로 배열을 사용하여 데이터를 저장하기 때문이다.
고유한 인덱스 값 설정
1.Division Method: 나눗셈을 이용하는 방법, 입력값을 테이블의 크기로 나누어 계산하는 방식
2.Digit Folding: 각 Key 문자열을 Ascll코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용한다.
3.Multiplication Method: 숫자로 된 Key 값 K와 0과 1의 실수 A, 보통 2의 제곱수인 m을 사용하여 h(k)=(kAmod1) × m 공식으로 해시값을 만든다.
4.Universal Hashing: 다수의 해시함수를 만들어 집합 H에 넣어두고 무작위로 해시함수를 선택해 해시값을 만든다.
해시 값이 충돌하는 경우
이렇게 분리를 하더라도 해시값이 충돌할 가능성이 있다.
분리 연결법(Seperate Chaining)
분리 연결법은 동일한 버킷의 데이터에 대해 자료구조를 활용해 추가 메모리를 사용하여 다음 데이터의 주소를 저장하는 것이다.
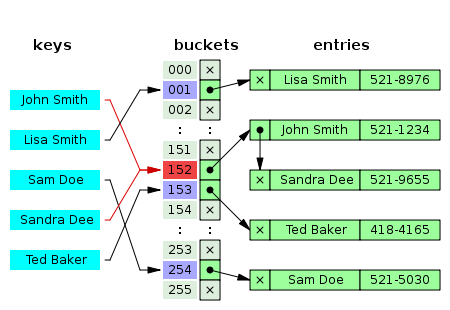
존 스미스 뒤에 산다라 리가 붙음
Self-Balancing Binary Search Tree 자료구조를 사용하여 Chaining 방식을 구현하였다.
자체 균형 이진 검색트리(Self Balancing Binary Search Tree) 가 무엇일까?
자체 균형 이진 검색트리는 임의의 항목 삽입 및 삭제에 직면하여 높이(depth)를 자동으로 작게 유지하는 노드 기반 이진 검색 트리이다.
굉장히 복잡한 이론이니 개념만 확인하는걸로 하자...
이렇게 Chaining 기법을 사용하게 되면 해시 테이블의 확장 없이 추가적인 메모리를 사용하여 간단하게 구현 및 삭제가 가능해지지만 데이터 수가 많아지면 동일한 버킷에 Chaining되는 데이터가 많아져서 그에 따른 캐시 효율성이 감소한다는 단점이 있다.
개방 주소법
비어있는 해시 테이블의 공간을 활용하는 방법
1.Linear Probing: 현재 버킷의 index로 부터 고정폭만큼씩 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장
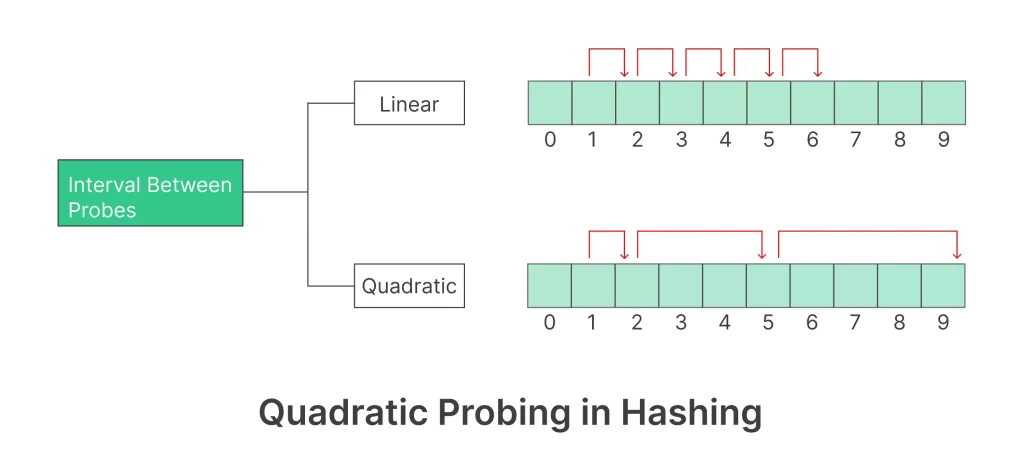
2.Quadratic Probing: 해시의 저장순서 폭을 제곱으로 저장하는 방식, 처음 충돌 발생시 1만큼 이후에 4, 9칸씩 옮기는 방식이다.
3.Double Hashing Probing: 해시된 값을 한번 더 해싱하여 해시의 규칙성을 없애버리는 방식, 새로운 주소를 할당하기 위해 더 많은 연산이 요구된다.
개방 주소법에서 데이터를 삭제하면 삭제된 공간은 Dummy Space(사용하지 않는 공간)로 활용되는데 그렇기에 Hash Table을 재정리 해주는 작업이 필요하다.
해시 테이블 관련 예시 코드
class HashTable {
constructor(size) {
this.table = new Array(size);
this.size = size;
}
_hash(key) {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash = (hash + key.charCodeAt(i)) % this.size;
}
return hash;
}
set(key, value) {
let index = this._hash(key);
if (!this.table[index]) {
this.table[index] = [];
}
this.table[index].push({ key: index, value });
}
get(key) {
let index = this._hash(key);
return this.table[index];
}
}
const hashTable = new HashTable(20);
hashTable.set("spartan", "스파르탄");
hashTable.set("node", "노드");
hashTable.set("tanspar", "스파르탄2");
console.log(hashTable.get("spartan"));
console.log(hashTable.get("node"));
분리 연결법을 통해서 해시 테이블을 구현하였다.
