지난번 tcav와 ace에서 이어진 논문이다. tcav도 생소했고 ace는 내용이 별로 없었는데 이번 논문은 너무 hardcore여서 제대로 이해한건지에 대한 의문뿐인 논문 공부였다. 논문의 부족한 이해 부분을 고려대학교 산업경영공학부 DSBA 연구실의 유튜브 영상을 통해 도움을 얻었다.
https://www.youtube.com/watch?v=-l8vqkCu91M&ab_channel=%EA%B3%A0%EB%A0%A4%EB%8C%80%ED%95%99%EA%B5%90%EC%82%B0%EC%97%85%EA%B2%BD%EC%98%81%EA%B3%B5%ED%95%99%EB%B6%80DSBA%EC%97%B0%EA%B5%AC%EC%8B%A4
이 논문의 발단은 인간이 아닌 자동적으로 추출한 concept가 DNN의 결과를 충분히 predictive하는지? 그렇다면 우리가 이 sufficiency를 어떨게 측정할지가 이 논문의 주요 관심사이다.
이 논문에서는 completeness score, conceptSHAP를 통해 해당 관심사들을 설명하고자한다.
problem setting:

학습된 DNN모델을 입력을 받는 파이부분과 파이 함수로부터 나온 값을 확률로 출력하는 h함수, 두 함수로 쪼갤 수 있다. 파이는 다시 입력 Xi의 분할된 조각인 Xij를 입력으로 받는 파이 함수(동그랑 땡?뭐라읽지?)들로 쪼개진다.

데이터와 concept vector와의 closeness는 내적을 통해 계산한다. 당연히 값이 클 수록 가깝다.
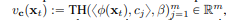
내적값이 베타보다 크면 그 값그대로 출력, 작으면 0으로 출력한다.
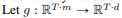
g는 t x m공간을 t x d로 변환하는 함수, concept score를 파이의 activation space로 매핑한다.

completeness score의 정의는 위와 같다. 기존 DNN모델의 예측과 concept score vc(x)를 사용했을때의 best predicting accuracy(vc(x)->gf로 매핑->h로 출력, sup가 상한을 뜻한다)를 비교하여 점수를 매긴다. ar은 0을 맞추기위한 상수이다.
Xor문제를 통해 completeness score의 예시를 논문에서 드는데 이 부분은 이해가 가지않았다.
기존 Tcav와 Ace의 한계점:
Tcav는 사람이 직접 concept를 한땀한땀 정의해서 학습시키고, Ace는 k-mean clustering으로 유사한 컨셉들끼리 묶는 방식으로 두 방식 모두 concept이 complete한지는 자신없다.
또 TcaV는 선형 분류를 통해 concept vector를 찾았는데 때문에 non-linear relationship을 갖는 concept를 찾는데 한계가 있다(Xor같은).
topic model이야기가 나오는데..
"토픽 모델링(Topic Modeling)이란 기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법이다."

concept의 interpretability를 향상시키기위해 regularizer를 이용해서 concept의 spatial dependency를 높인다.
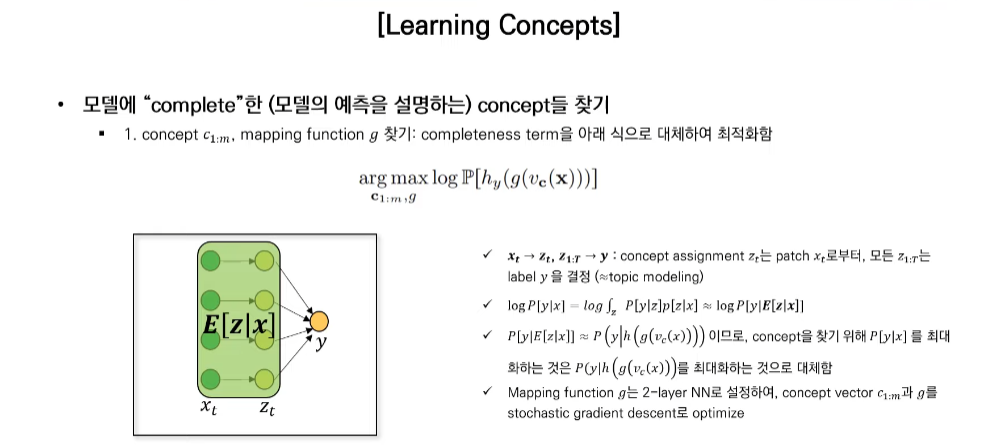
Xt->Zt->y
log likelyhood인 logP[y|x]를 최대화하는건 log P(y|h(g(vc(x))))를 최대화하는것과 동일,
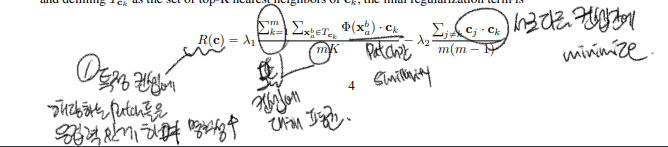
patch간 similarity를 극대화, 서로 다른 컨셉간 similarity를 최소화한다(이 부분 왜 이런지,어떻게 하는지 둘다 모르겠음.. )
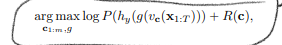
최종 규제까지 적용한 식, c1~cm의 completness score
conceptSHAP
우리가 이제까지는 모든 concept들을 이용해 score를 측정하는 법을 배웠다면 이제는 concept집합속 각 concept이 얼마나 중요한지를 conceptSHAP를 통해 알아 낼 것이다. 이는 게임이론의 shapely value를 이용한다.
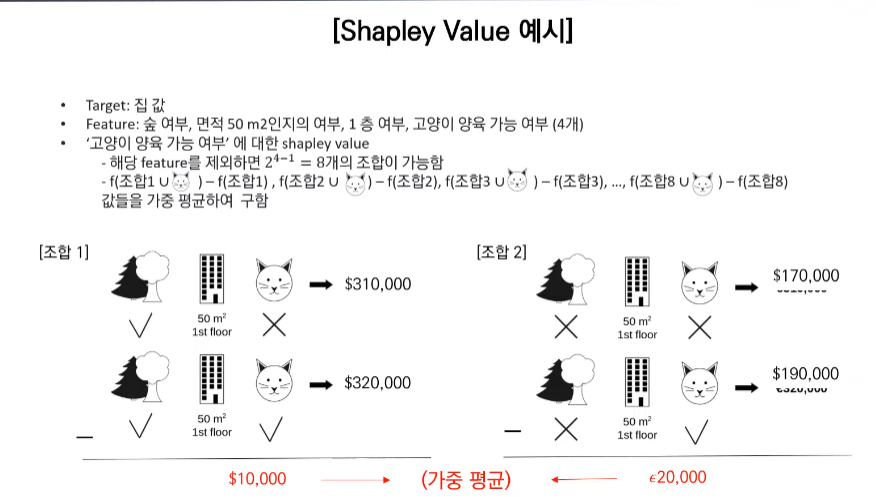
어떤 concept집합 Cs={c1,c2,,,,cm}이 있으면 어떤 concept ci의 중요도는 집합 Cs에서 ci를 제외한 concept들의 조합과 해당조합과 ci를 합친것에 차이를 구하면 ci의 중요도를 파악할 수 있다. ci의 유무에 따른 결과를 통해 ci의 중요도를 측정한다.

completeness score는 다음과 같이 정의되고
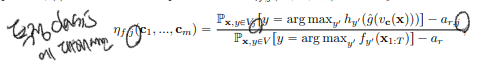
특정 class j의 completeness score는 다음과 같이 정의가 된다.