[블록체인] 블록체인 암호화 기술

HwangJerry·2023년 4월 29일
blockchain
0
post-thumbnail

암호화 기술 개요

암호화 매커니즘을 간단히 요약하면 다음과 같습니다.

송신자가 평문을 암호화 키를 통해 암호문으로 바꿔서 그 내용을 숨기고, 수신자가 이를 다시 암호화 키를 통해 평문으로 확인할 수 있게 합니다.

이 과정에서 암호화 키를 어떻게 설정하느냐는 다음 두 가지 방법이 대표적입니다.

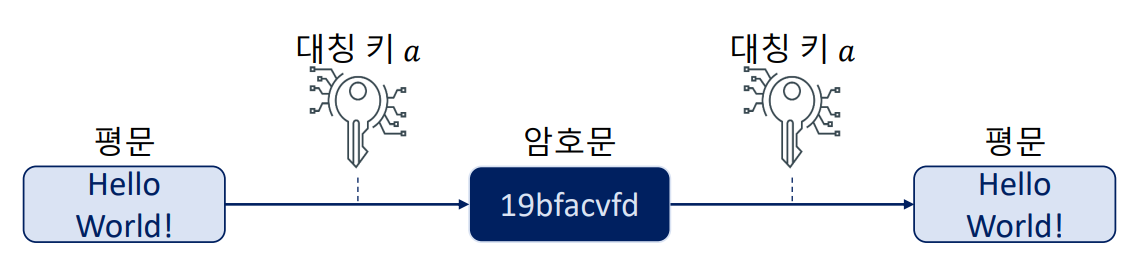
  • 대칭 키:
    동일한 키로 암호화와 복호화가 가능하도록 이용됩니다.

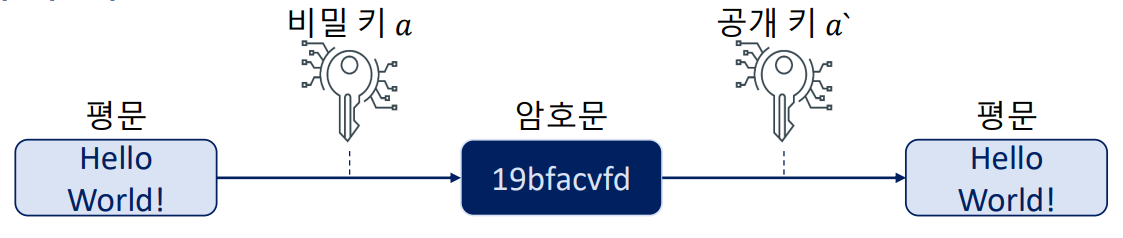
  • 비대칭 키:
    비밀 키로 평문을 암호화하고, 공개 키로 복호화가 가능합니다. 해당 비밀 키와 공개 키는 매핑되어 있어서, 특정 공개 키로 복호화가 가능함을 통해 해당 정보가 비밀 키의 주인이 송신한 정보임을 검증할 수 있습니다. 이를 서명이라고 합니다.

공개키 암호화 알고리즘

RSA와 ECC는 대표적인 공개키 암호화 방식입니다. 두 알고리즘 모두 암호화 및 복호화에 사용되는 공개 키와 개인 키 쌍을 가지고 있습니다. 공개 키는 암호화 및 서명 검증에 사용되며, 개인 키는 복호화 및 서명 생성에 사용됩니다.

RSA

RSA(Rivest-Shamir-Adleman)는 공개 키와 비밀 키 쌍을 사용한 비대칭 키 방식으로, 어떤 키로 암호화하느냐에 따라 다른 방식을 제공합니다.

이 알고리즘은 큰 수의 소인수 분해가 어렵다는 수학적 특징을 사용하고 있습니다. 따라서 RSA의 보안성은 키의 길이가 충분히 길어야 하는 것에 의존적입니다.

RSA-2048은 2048bit를 키로 사용하는 가장 대중적인 알고리즘으로, 인터넷 뱅킹과 공인인증서 등에 널리 사용되고 있습니다.

키 생성:
➢ 임의의 소수 p, q 선택 // 두 개의 큰 소수
➢ 𝑛 = 𝑝 × 𝑞 // n은 모듈러스로 사용
➢ 𝜑(𝑛) = (𝑝 − 1)(𝑞 − 1) 계산 // 오일러 토타 함수
➢ 임의의 정수 d를 선택
➢ (𝑔𝑐𝑑 (𝜑(𝑛), 𝑑) = 1, 1 < 𝑑 < 𝜑(𝑛)) // 개인키 지수 d
➢ 𝑒 = 𝑑^(−1) 𝑚𝑜𝑑 𝜑(𝑛) 계산 // 공개키 지수 e
➢ 공개키 𝐾𝑈 = {𝑒, 𝑛} 와 개인키 𝐾𝑅 = {𝑑, 𝑛}

암호화:
➢ 평문 메세지 M을 숫자로 변환 // M < n
➢ 𝐶 = 𝑀^𝑒 (𝑚𝑜𝑑 𝑛) // 암호화된 메세지 C

복호화: 
➢ 암호화된 메세지 C를 받음
➢ 𝑀 = 𝐶^𝑑 (𝑚𝑜𝑑 𝑛)

◦ 모듈러스 : 나머지 연산에서 사용되는 양의 정수
◦ KU : Key for public Use
◦ KR : Key for Restricted use

ECC

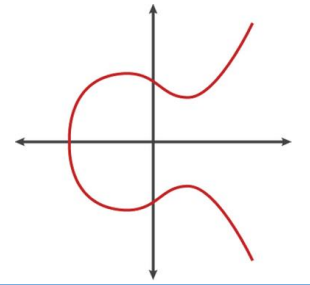
타원 곡선 암호(Elliptic Curve Cryptography)를 의미하며, RSA의 대체제로 1985년에 제안된 알고리즘입니다.

기존 RSA는 충분한 보안성을 위해 1000bits 이상의 큰 숫자를 키로 사용해야 했으므로, 연산량이 많아지는 것이 큰 단점으로 작용하였습니다.

ECC는 더 적은 bits로 동등한 수준의 안전성을 가지므로 좋은 대안으로 적용되었습니다.

비트코인에서는 secp256k1이라는 타원 곡선을 이용하여 ECC를 활용합니다.

secp256k1 수식 : y^2 mod p = (x^3 + 7) mod p

ECC 암호화 알고리즘은 다음과 같습니다.

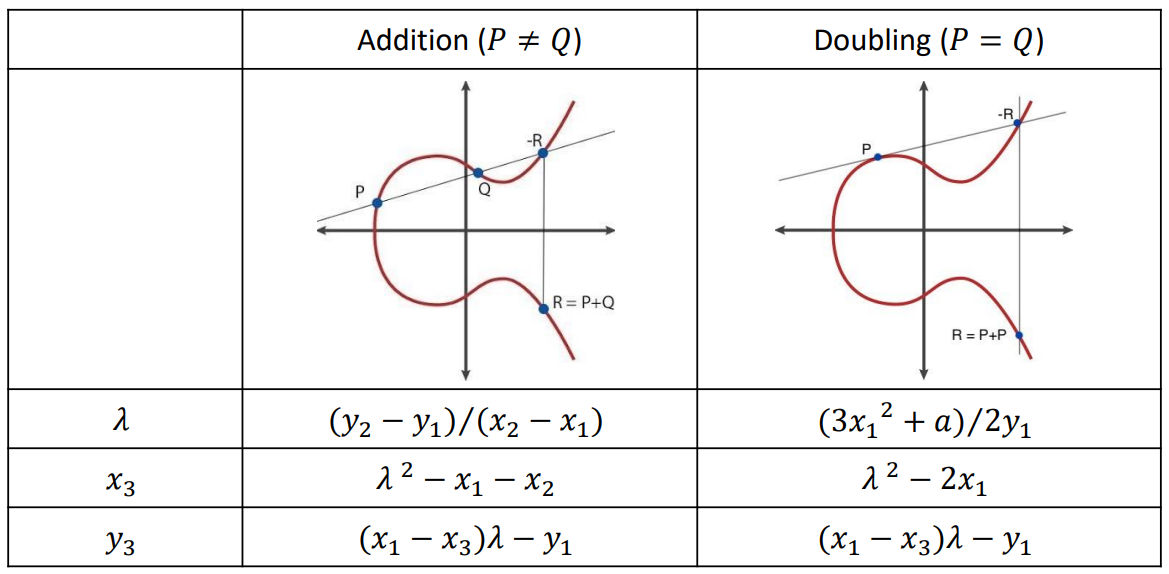
➢ 임의의 타원곡선 𝑦^2 = 𝑥^3 + 𝑎𝑥 + 𝑏 (𝑚𝑜𝑑 𝑝)과 소수값 𝑝 정의
◦ 이 때 𝑝는 매우 큰 소수
➢ 타원곡선 상의 시작점 𝐺 정의
➢ 개인키 값 𝐾를 정의
◦ 이 때 𝐾는 2^(256) 정도의 매우 큰 수로,987난수 시스템을 활용함
➢ 공개키 𝑅 = 𝐺 ∗ 𝐾
➢ 이 때, 유한한 좌표를 구하기 위해 
모듈러 연산을 통해 갈루아 필드 상에서 표시

ECC 암호화 알고리즘의 예시를 들어봅시다.

임의의 타원곡선 y^2 = x^3 + 2x + 3(mod 5), p = 5

1. 갈루아 필드 상에서 유효한 좌표 구하기:
◦ x = 0 | y^2 = 3 -> y는 존재할 수 없음.
◦ x = 1 | y^2 = 6 -> y^2 = 1 mod 5 -> y = 1, 4
◦ x = 2 | y^2 = 15 -> y^2 = 0 mod 5 -> y = 0
◦ x = 3 | y^2 = 36 -> y^2 = 1 mod 5 -> y = 1, 4
◦ x = 4 | y^2 = 75 -> y^2 = 0 mod 5 -> y = 0

따라서 가능한 시작점은 (1,1), (1,4), (2,0), (3,1), (3,4), (4,0)입니다.
임의의 시작점으로 G(1,4)와 개인키 K=3을 가정하고 풀어보겠습니다.

2. 
◦ 공개키 R = G * K 입니다.
◦ 여기서 K = 3이므로 R = 3G를 구하면 됩니다.
◦ 3G = G + G + G = G + 2G이므로 우선 2G를 구해보겠습니다.

3. 
2G = G + G = (1,4) + (1,4)
즉, P = Q = (1,4)인 경우이므로,

➢ 𝜆 = 3x^2 + a / 2y (mod 5) = 5/8 mod 5 = 5*8^(-1) mod 5 = 0*8^3 mod 5 = 0
➢ x3 = 𝜆^2 - 2x1 (mod 5) = 0 - 2 (mod 5) = 3
➢ y3 = 𝜆(x1 - x3) - y1 (mod 5)= 0(1-3) - 4 (mod 5) = 1
따라서 2G = (3,1)입니다.

4.
이제 3G를 구해봅시다.
3G = G + 2G = (1,4) + (3,1)
즉, P != Q 인 경우이므로,

➢ 𝜆 = (y2 - y1) / (x2 - x1) (mod 5) = (1-4)/(3-1) mod 5 = (-3/2) mod 5 = 2*2^(3) mod 5 = 1 
➢ x3 = 𝜆^2 - x2 - x1 (mod 5) = 1^2 - 3 - 1 (mod 5) = 2
➢ y3 = 𝜆(x1 - x3) - y1 (mod 5) = 1(1-2) - 4 (mod 5) = 0
따라서 3G = (2,0)입니다.

암호화 기술 활용

해시(Hash)는 어떠한 데이터를 고정된 길이의 고유한 문자열로 변환하는 과정이나 결과를 가리키는 용어입니다.

마치 데이터들의 지문과도 같다고 말할 수 있습니다. 예를 들어, 2개의 메세지가 동일한 것인지 조사할 때 해시를 사용한다면 메세지를 직접 비교하는 것이 아닌 메시지의 "지문"을 비교하는 것과 같다는 것이죠.

해시 함수는 임의의 데이터(문자열, 이미지, 음성 등)에서 고정된 길의의 결과값을 빠르게 출력합니다.

해시 함수는 다음과 같은 특징을 가집니다.

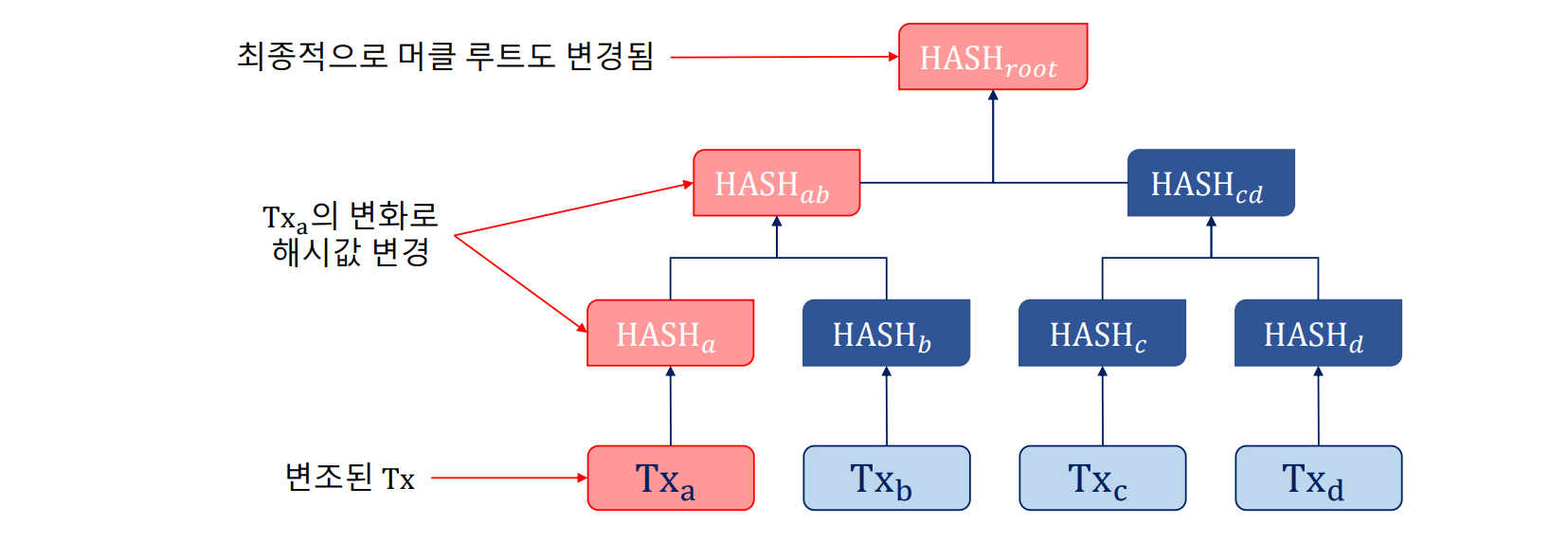
  • 데이터의 아주 작은 변화도 해시값의 큰 변화로 이어진다.
  • 일방향성을 가지므로, 해시값에서 메시지를 알아낼 수 없다.
  • 충돌이 "거의" 발생하지 않는다.

    [충돌] : 서로 다른 두 메시지가 같은 해시 값을 갖는 것

비트코인 주소 생성

비트코인 주소는 디지털 지갑에서 송금을 받기 위한 고유한 식별자 역할을 합니다.

사용자의 공개 키 정보를 포함하고 있지만, 개인 키 정보는 포함하지 않습니다.

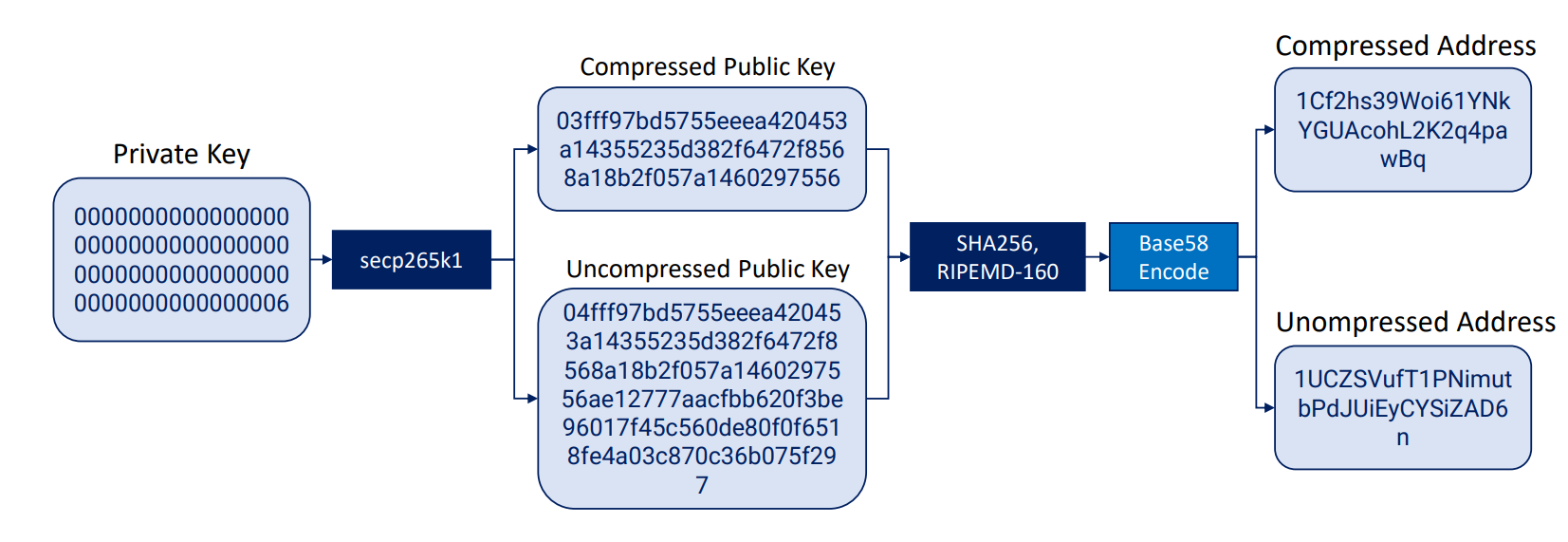
  1. 개인 키 생성 :
    안전한 난수 생성기를 사용하여 256비트 길이의 무작위 수를 생성하고, 해당 수가 유효성 검사를 통과하면 이를 개인 키로 사용합니다.

  2. 공개 키 생성 :
    타원곡선 암호화(ECC)를 사용하여 개인 키로부터 압축&비압축 포맷의 공개 키를 생성합니다.

  3. 공개 키 해싱 :
    생성된 공개 키를 해시 함수인 double-SHA-256을 통해 공개 키를 해싱한 후, 그 결과를 다시 RIPEMD-160 해시 함수에 통과시킵니다.

    위 과정들을 통해 생성된 공개 키와, 그 해시 값은 반대 방향으로 변환할 수 없습니다. 하지만 아래 인코딩의 경우 공개 키 해시와 지갑 주소 간 상호 변환이 가능한 동일 정보를 뜻합니다.

  4. Base58 인코딩 :
    공개 키 해시 앞에 버전 바이트를 합친 뒤, Base58 인코딩으로 변환합니다. 이렇게 인코딩된 결과가 최종 비트코인 주소입니다.

    압축된 주소는 주소 생성 과정에서 공개 키가 압축된 형식을 사용하고, 압축되지 않은 주소는 공개 키가 압축되지 않은 형식을 사용합니다.

비트코인 거래 서명


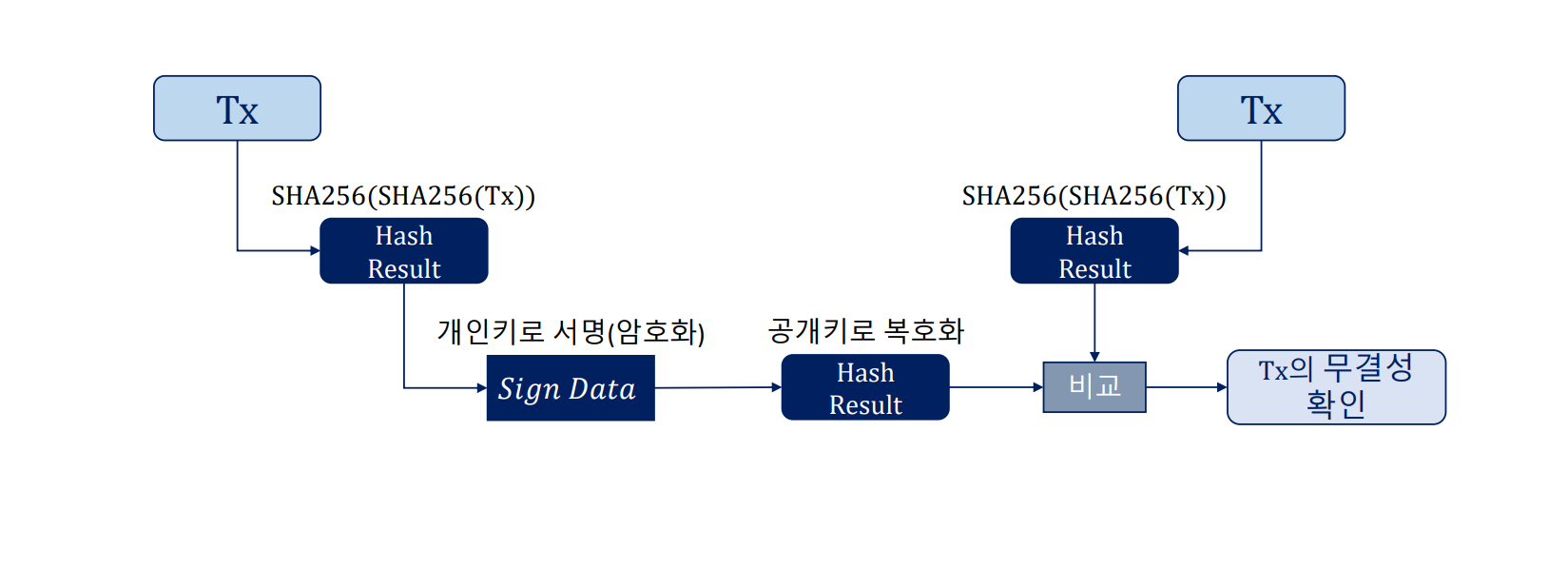
서명이란 송신자가 개인 키를 이용하여 데이터를 암호화하는 것을 말합니다. 이후 공개키로 복호화가 가능하고, 거래를 해시한 값을 대조함으로써 거래의 위변조를 확인할 수 있습니다.

비트코인의 거래 서명 과정은 다음과 같습니다.

  1. 거래 생성 :
    비트코인을 송금하려는 사용자가 거래를 생성합니다. 거래에는 입력(송신자 주소, 송신자가 사용할 UTXO), 출력(수신자 주소, 전송할 금액) 및 수수료 등이 포함됩니다.

  2. 거래 해싱 :
    생성된 거래 데이터를 바탕으로 SHA-256를 이용하여 해시값을 생성합니다. 이 해시 함수를 통해 거래의 모든 정보를 처리하고, 256비트 길이의 고유한 출력을 생성합니다.

  3. 서명 생성 :
    송신자의 개인 키를 사용하여 거래 해시에 서명합니다. 비트코인에서 사용되는 디지털 서명 알고리즘은 ECC를 기반으로 하는 ECDSA(Elliptic Curve Digital Signature Algorithm)입니다.

  4. 서명 추가 :
    생성된 서명을 원래 거래의 입력에 추가합니다. 이렇게 하면 거래가 서명된 거래로 변환됩니다.

  5. 거래 전송 :
    서명된 거래를 비트코인 네트워크에 전송하여 블록체인에 포함되도록 요청합니다.

  6. 거래 검증 :
    전파된 거래는 노드와 마이너들에 의해 검증되고, 올바른 서명 및 자금이 있는 경우 블록에 포함되고, 블록체인에 기록됩니다.

double-SHA-256 알고리즘 적용 예시

  1. 블록 헤더에 double-SHA-256 알고리즘을 적용해 헤더 해시 생성
    -> 헤더 해시는 이전 블록을 가리키는 포인터와 블록의 유효성을 검증할 때 사용
  1. 트랜잭션에도 double-SHA-256 알고리즘을 적용해 UTXO를 찾을 때, 또는 TxID로써 활용
    -> 만약 트랜잭션 중 하나가 위변조된다면 머클 트리에도 해시가 적용되어 있으므로, 머클 루트가 변경되게 되니 결국 위변조가 불가능
profile
HwangJerry
알고리즘 풀이 아카이브
이전 포스트

[블록체인] 블록체인 트릴레마

다음 포스트

[블록체인] 노드와 블록

0개의 댓글