경사하강법 - 1

JH_CHOI·2022년 1월 18일

ai math

경사하강법

중요 개념

미분의 개념
그래디언트 벡터

목표

접선의 기울기를 이용해서 함수의 최솟값으로 점을 이동시키는 원리를 알아보고 이를 바탕으로 경사하강법의 알고리즘과 수식을 이해해보자.

권고사항

※ 특히 변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d-차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡고 가자.

미분이란?

미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용하는 기법입니다.
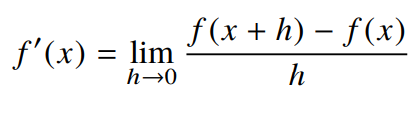
최근엔 컴퓨터로도 미분을 계산할 수 있습니다.
- sympy.diff를 가지고 미분을 계산할 수 있습니다.
미분은 함수 f의 주어진 점 (x, f(x))에서의 접선의 기울기를 구하기 위해 계산하는 것으로 이해할 수 있습니다.
한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가하는지/감소하는지 알 수 있다.
- 함수값을 증가시키고 싶다면 미분값을 더한다.
- 함수값을 감소시키고 싶다면 미분값을 뺀다.
미분값을 더하면 경사상승법(gradient ascent)이라 하며 함수의 극대값의 위치를 구할 때 사용한다.
- 목적함수를 최대화할 때 사용한다.
미분값을 빼면 경사하강법(gradient descent)이라 하며 함수의 극소값의 위치를 구할 때 사용한다.
- 목적함수를 최소화할 때 사용한다.
경사상승/하강 방법은 극값에 도달하면 움직임을 멈춘다.
- 극값에선 미분값이 0이므로 더 이상 업데이트가 안된다. 그러므로 목적함수 최적화가 자동으로 끝난다.

# gradient : 미분을 계산하는 함수
# init : 시작점
# lr : 학습률 (learning rate)
# eps : 알고리즘 종료 조건 (epsilon)

var = init
grad = gradient(var)
while (abs(grad) > eps):
    var = var - lr * grad
    grad = gradient(var)

코드 해석

컴퓨터로 계산할 시 미분이 정확히 0이 되는 것은 불가능하므로 eps보다 작을 때 종료하는 종료 조건을 넣어줘야 한다.
lr은 learning rate(학습률)의 약자로, 미분을 통해 업데이트하는 속도를 조절한다.
종료 조건이 성립하기까지 미분값을 계속 업데이트 한다.

변수가 벡터일 때는?

벡터가 입력인 다변수 함수의 경우는 편미분(partial differentation)을 사용한다.

e_i는\ i번째\ 값만\ 1이고\ 나머지는\ 0인\ 단위벡터

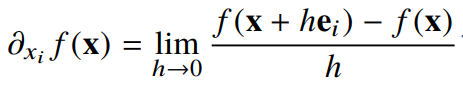
즉, i번째의 방향에서의 변화율만을 계산할 수 있다
각 변수 별로 편미분을 계산한 그래디언트(gradient) 벡터를 이용하여 경사하강/상승법에 사용할 수 있다.

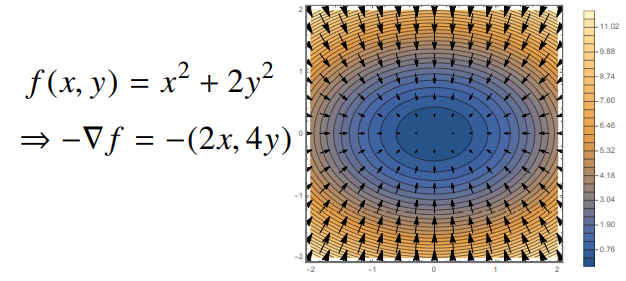
$앞서\ 사용한\ 미분값인\ f^\prime(x) 대신\ \nabla f를\ 사용하여\ 변수\\ x=(x_1, ...,x_d)를\ 동시에\ 업데이트\ 가능합니다.$

그래디언트 벡터

그래디언트 벡터 : 각 변수 별로 편미분을 계산한 벡터

-\nabla f는\ \nabla(-f)와 같고\ 이는\ 각\ 점에서\ 가장\ 빨리\ 감소하게\ 되는\ 방향을\ 말한다.

# gradient : 그래디언트 벡터를 계산하는 함수
# init : 시작점
# lr : 학습률 (learning rate)
# eps : 알고리즘 종료 조건 (epsilon)

var = init
grad = gradient(var)
while (norm(grad) > eps):
    var = var - lr * grad
    grad = gradient(var)