벡터

---

중요 개념

• 벡터의 개념
• 벡터의 연산
• 벡터의 노름
• 두 벡터 사이의 거리와 각도
• 벡터의 내적

목표

벡터는, 딥러닝에서 매우 중요한 선형대수학의 기본 단위가 되고, 앞으로 배울 numpy에서도 굉장히 많이 사용되는 연산이기 때문에 확실하게 잡고 가야 할 개념이다. 벡터간의 연산을 단순히 숫자 계산으로 끝내기보단, 공간에서 어떤 의미를 가지는지를 이해하면서 공부해보자!

권고사항

노름이나 내적 같은 개념 또한, 그 자체로 가지는 기하학적인 성질과 이것이 실제 머신러닝에서 어떻게 사용되는지를 같이 생각해보시면서 공부하면 도움이 많이 될 것이다!

벡터란?

• 벡터는 숫자를 원소로 가지는 리스트 또는 배열입니다.

x = [1, 7, 2]

# numpy에서 array를 표현할 때 주로 행벡터로 표현한다.
x = np.array([1, 7, 2])

# 벡터에 있는 요소(숫자)의 갯수를 차원이라고 한다.
# 3차원
x = [1, 7, 2]

• 벡터는 공간에서 한 점을 의미합니다.
• 벡터는 원점으로부터의 상대적 위치를 나타냅니다.

벡터의 연산

• 벡터에 숫자를 곱해주면 길이만 변합니다. (=스칼라곱)
• 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있습니다.
• 벡터끼리 같은 모양을 가지면 성분곱(Hadamard product)을 계산할 수 있습니다.
• 두 벡터의 덧셈은 다른 벡터로부터의 상대적 위치이동이라고 말할 수 있습니다.

벡터의 노름

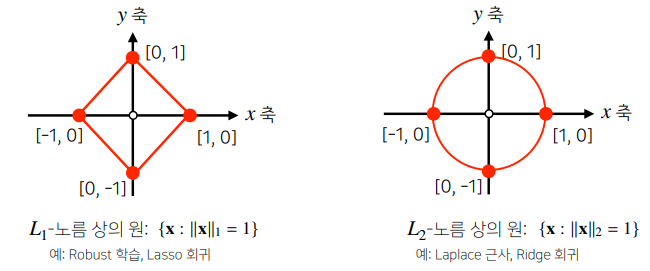
• 벡터의 노름(norm)은 원점에서부터의 거리를 말합니다.

  $L_1노름은\ 각\ 성분의\ 변화량의\ 절대값을\ 모두\ 더합니다.$
  $L_2노름은\ 피타고라스\ 정리를\ 이용해\ 유클리드\ 거리를\ 계산합니다.$

왜 다른 노름을 소개할까?

• 노름의 종류에 따라 기하학적 성질이 달라집니다.
• 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘 다 사용합니다.
  

두 벡터의 거리

$L_1, L_2노름을\ 이용해\ 두\ 벡터\ 사이의\ 거리를\ 구할\ 수\ 있습니다.$

• 두 벡터 사이의 거리를 구할 때 벡터의 뺄셈을 이용합니다.
  • 뺄셈을 거꾸로 해도 거리는 같다는 점!

두 벡터의 각도

• 두 벡터 사이의 거리를 이용하여 각도도 계산이 가능하다!
• 제2 코사인법칙에 의해 두 벡터 사이의 각도를 계산할 수 있다
• 분자를 쉽게 계산하는 방법이 내적이다.

$제2\ 코사인법칙:\ \cos\theta= \frac{2<x, y>}{2||x||_2||y||_2} \\ 내적:\ <x,y>= \sum\limits_{i=1}^{d}{x_iy_i}$

벡터의 내적

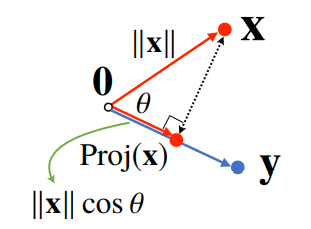
• 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.
  

  $Proj(x)의\ 길이는\ 코사인법칙에\ 의해\ ||x||\cos\theta가 된다.$

• Proj(x)는 벡터y로 정사영된 벡터x의 그림자를 의미한다.

  $내적은\ 정사영의\ 길이를\ 벡터y의\ 길이\ ||y||만큼\ 조정한\ 값이다.$

  $$

• 내적은 두 벡터의 유사도(similarity)를 측정하는데 사용가능하다.