#1 로지스틱 회귀

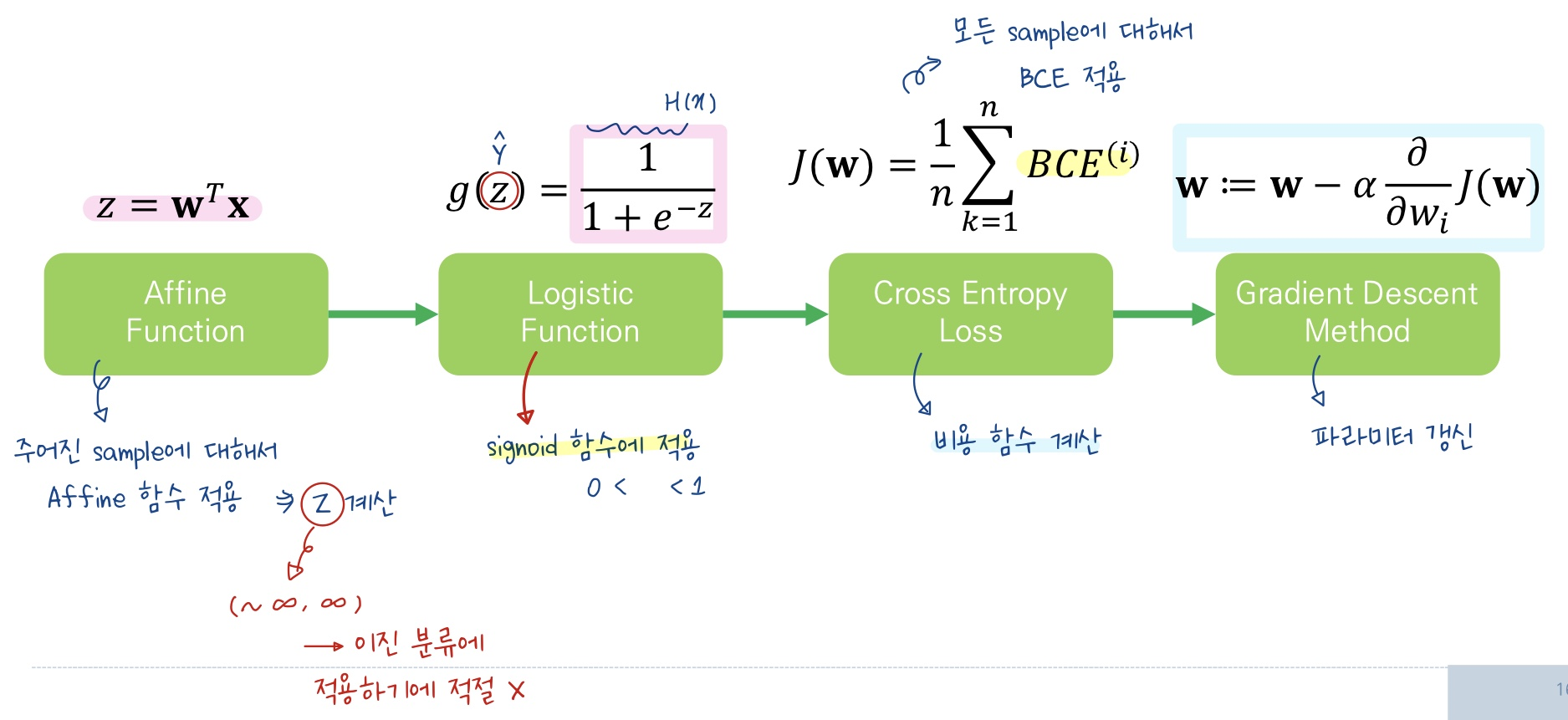
✔️ 선형 회귀란?

'선형 회귀'는 주어진 데이터를 가장 잘 나타내는 직선을 구해 새로 들어올 데이터에 대해 예측을 수행하는 과정

✔️ 이진 분류란 ?

부류가 두개인 분류 문제를 의미

• 분류를 한다는 것은 각 클래스(부류)를 구분할 수 있는 경계를 구하는 것

💥 분류 문제에서 선형 회귀를 사용하게 되면 발생하는 문제점 💥

😰 기울기 값 변화의 문제

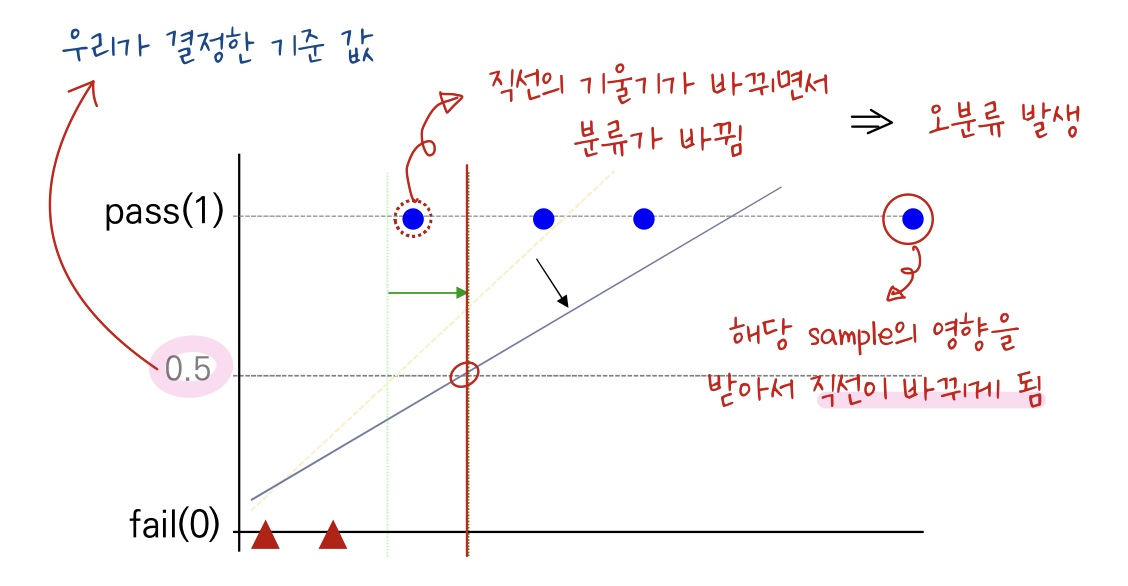
• 평균에서 벗어나는 데이터가 들어오게 되면 직선에 영향을 주게 되면서 기울기 값이 변하게 된다.

• 기울기 값이 변하게 되면 직선의 모양이 바뀌어 오분류가 생기게 된다 😭

• 결국, Sample들의 분류가 어떻게 되느냐에 따라서 오분류가 되는 경우가 발생한다.

😰 출력 값 범위의 문제

• 선형 회귀의 경우에는 가중치 값이 양수 일때 x의 값이 증가하게 되면 y의 값도 무한히 증가하거나 무한히 작아지는 수를 가질 수 있게 된다.

• 이진분류의 경우에는 y의 값이 0또는 1의 값을 가져야 하는데 출력 값의 범위가 (-∞, ∞)까지의 범위를 갖게 된다면 매번 적용해 줄 때마다 기준 값을 변경하여 적용해 줘야 한다.

• 값이 너무 커버리면 기준을 찾기가 어려워지고 분류문제 적용에 문제가 생긴다.

따라서 모델 출력값의 범위를 0~1사이로 지정해주는 '로지스틱 회귀'를 사용하는 것!

• 로지스틱 회귀의 경우에는 시그모이드를 기반으로 이진분류를 수행한다고 생각하면 된다.

• 시그모이드 함수를 기반으로해서 모델을 생성하는 것이며 '이진 분류'를 목적으로 한다.

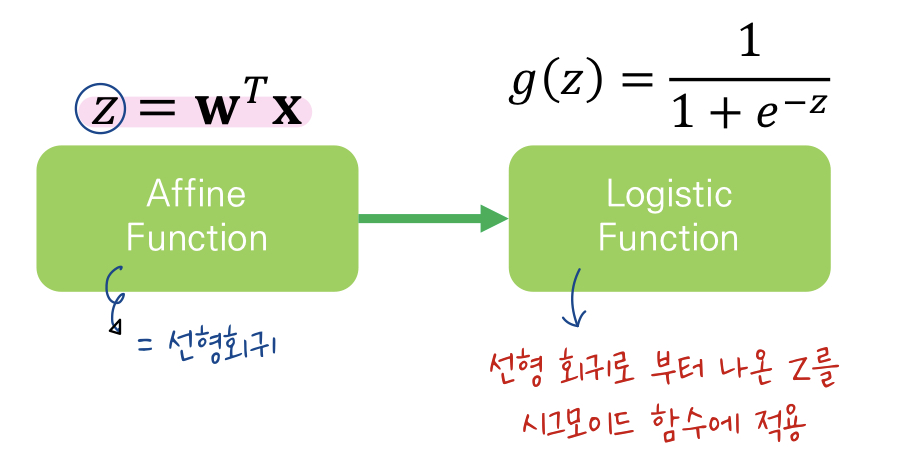
• 어파인 함수을 통해서 y의 값을 구하고 난뒤 모델 출력 값을 변경해 주는 시그모이드 함수를 적용하여 모델의 출력 범위를 변경해 주는 것이다.

✔️ 로지스틱 회귀의 cost function

• 로지스틱 회귀의 비용함수의 경우에는 선형 회귀에서 사용하는 mse를 적용하는 경우 이론상으로는 최소의 값을 많이 가지는 상태가 된다.

• 학습 방법에 따라 로컬 최소에 도달하게 되면 더 이상의 이동이 이루어지지 않아 정확한 학습이 불가능해진다.

따라서 사용하는 cost function은 'BCE(Binary Cross Entropy)'이다.

• 매끈한 포물선형 비용함수를 만들기 위해서 해당 함수를 사용한다.

• BCE의 경우엔 포물선 형태를 띄기 때문에 어떤 지점에서 시작하더라도 반복을 통해 궁극적으로 가장 최소의 값을 찾을 수 있다 😍

• BCE에서도 경사 하강법을 이용하여 최적의 파라미터를 찾기 위해서 학습한다.

🌞 Review