❤️ Logistic regression의 결과 값은 '확률값'❗❗ 따라서, 이진 분류를 위해서 각 부류의 분류의 기준이 되는 결정 임계값이 필요하다 ❕❕
✔️ 혼동 행렬이란?
혼동 행렬의 경우에는 예측값과 실제 값의 상관관계를 나타내며 오류의 경향성을 분석하는데 사용하는 행렬이다.
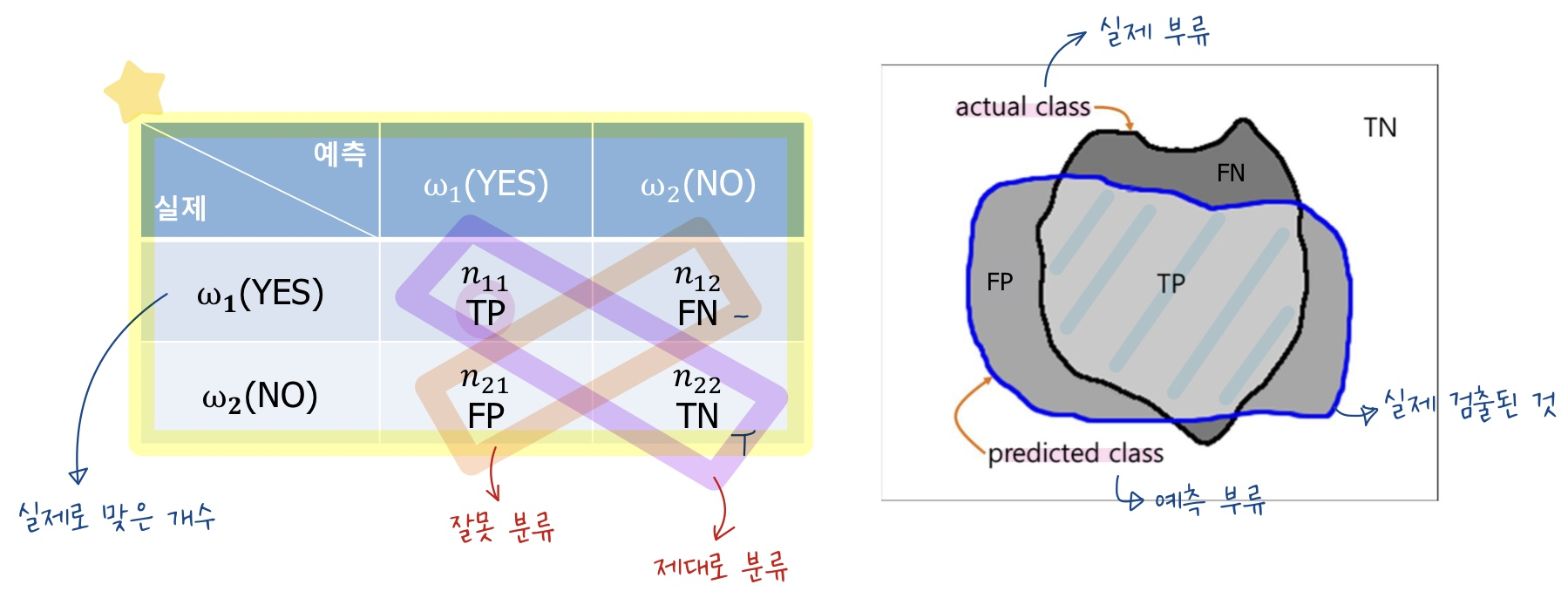
- 일반적으로 이진 분류에서 많이 사용되지만 다중 분류에서도 사용은 가능하다 💕
✔️ 각 문제에서의 기준
1. 분류 문제의 기준 = 정확도(accuracy)
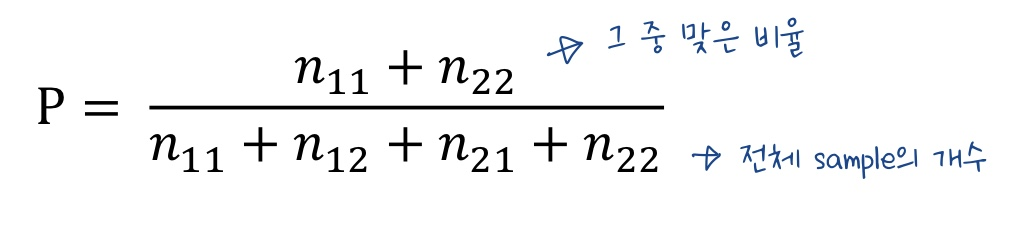
-
정확도는 전체 비율 중에서 실제로 내가 맞게끔 예측한 것의 비율을 의미한다.
-
정확도의 경우 검출에서도 사용이 가능하다.
2. 검출 문제의 기준 = 참 긍정률(true positive rate)과 거짓 긍정률(false positive rate)
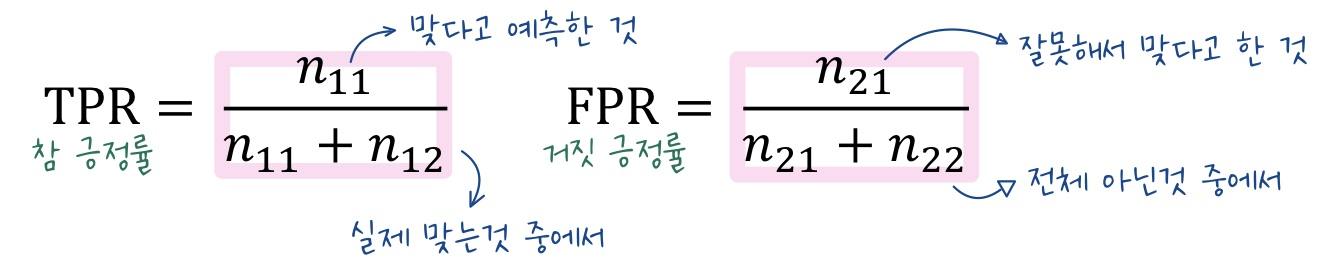
-
참 긍정률이란 실제로 맞는 것 중에서 내가 맞다고 예측한 비율을 의미한다.
-
거짓 긍정률이란 실제로 틀린 것 중에서 내가 맞다고 예측한 비율을 의미한다.
-
분류 문제에서도 해당 기준의 사용이 가능하다.
3. 검색 문제의 기준 = 정밀도(precision)와 재현률(recall)
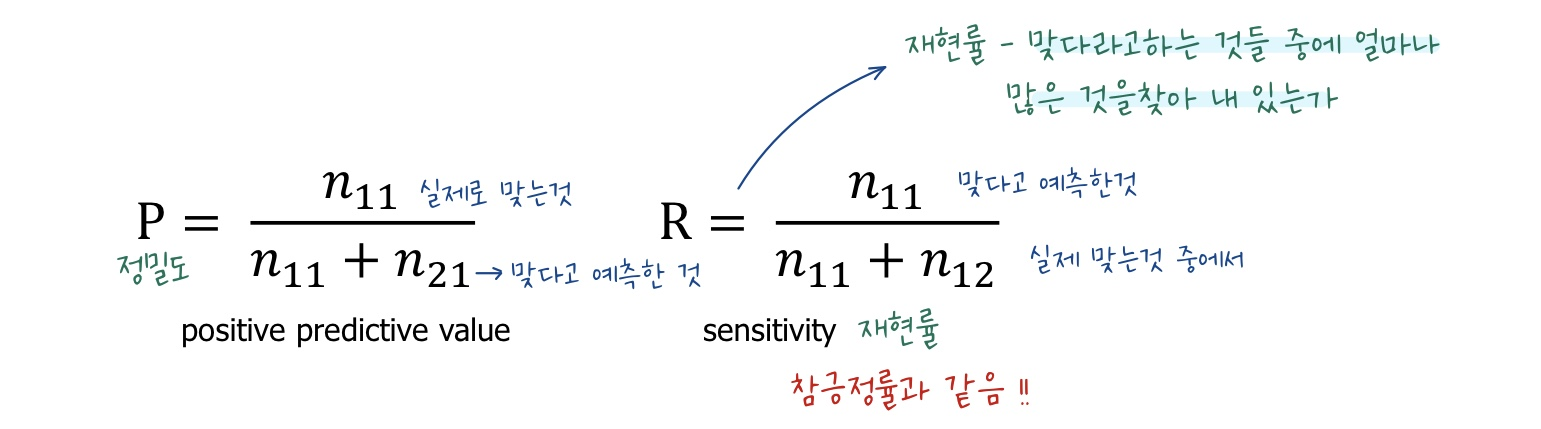
-
정밀도는 실제로 내가 예측한 것들 중에서 실제로 맞는 비율을 의미한다.
-
재현율은 참 긍정률과 구하는 방법은 같다.
-
재현율은 실제 중에서 얼마나 많은 것을 찾아냈는가에 대한 비율을 구하는 것이다.
-
정밀도와 재현율의 관계는 서로 반비례 관계를 나타낸다.
👍 정밀도와 재현률의 관계
- 분류 임계값을 기준으로 정밀도와 재현률 두개 사이의 관계를 설명 할 수 있다.
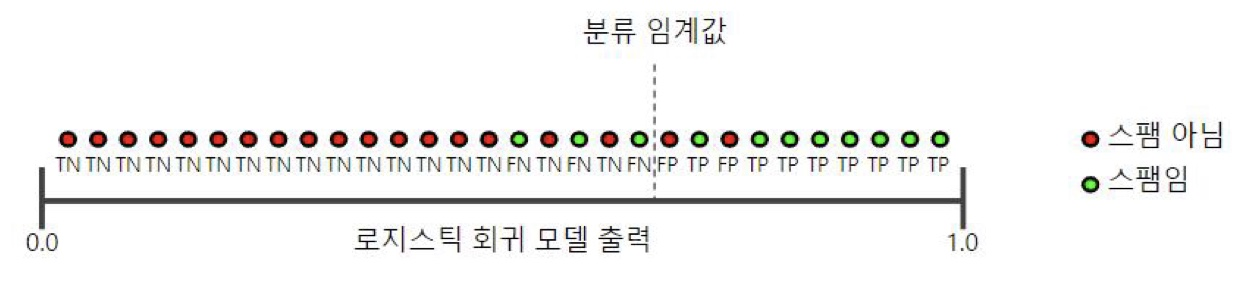
🚩 임계값이 작은 경우
-
임계값이 작아지게 되면 기준이 완화가 되어 많은 검색이 이루어진다.
-
많은 분류가 이루어졌기 대문에 그 중 실제에 해당하는 것들의 비율이 높아지게 되면서 재현률의 비율이 증가하게 된다.
-
반면, 많은 검색들 중 실제로 긍정인 것 중에서 긍정이라고 정확하게 판단한 비율이 줄어들게 되기 때문에 정밀도는 줄어들게 된다.
🚩 임계값이 큰 경우
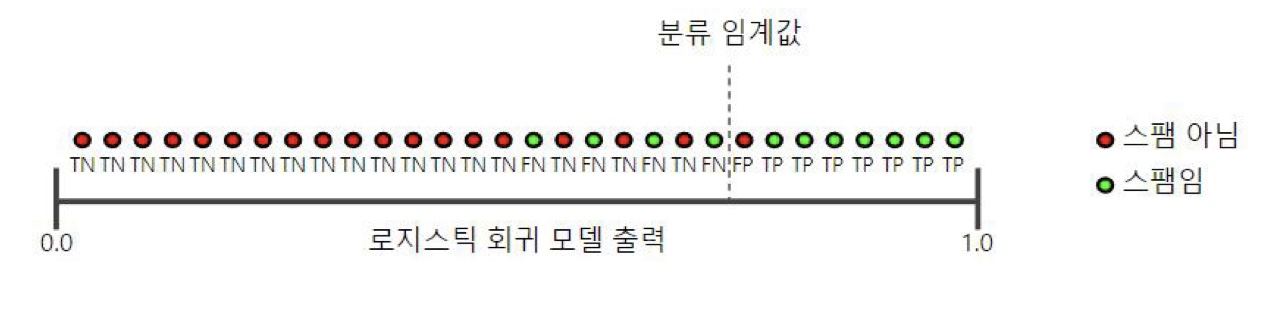
-
임계값이 커지게 되면 기준이 엄격하게 적용하게 된다.
-
따라서 전체에서 내가 맞다고 예측해야하는 상황이 줄어들게 되면서 재현율의 값이 줄어들게 된다.
-
전체 분류하는 긍정의 개수가 줄어들게 되면서 실제인 것 중에서 맞게 끔 잘 판단한 비율이 높아지게 되고 정밀도의 값이 증가하게 된다.
결정 임계값 만으로는 성능을 파악하기에는 한계가 존재 ❗
👍 그래서 사용하는 두 가지의 도구를 사용 - ROC 곡선, Precision-Recall 곡선
⚡ ROC 곡선
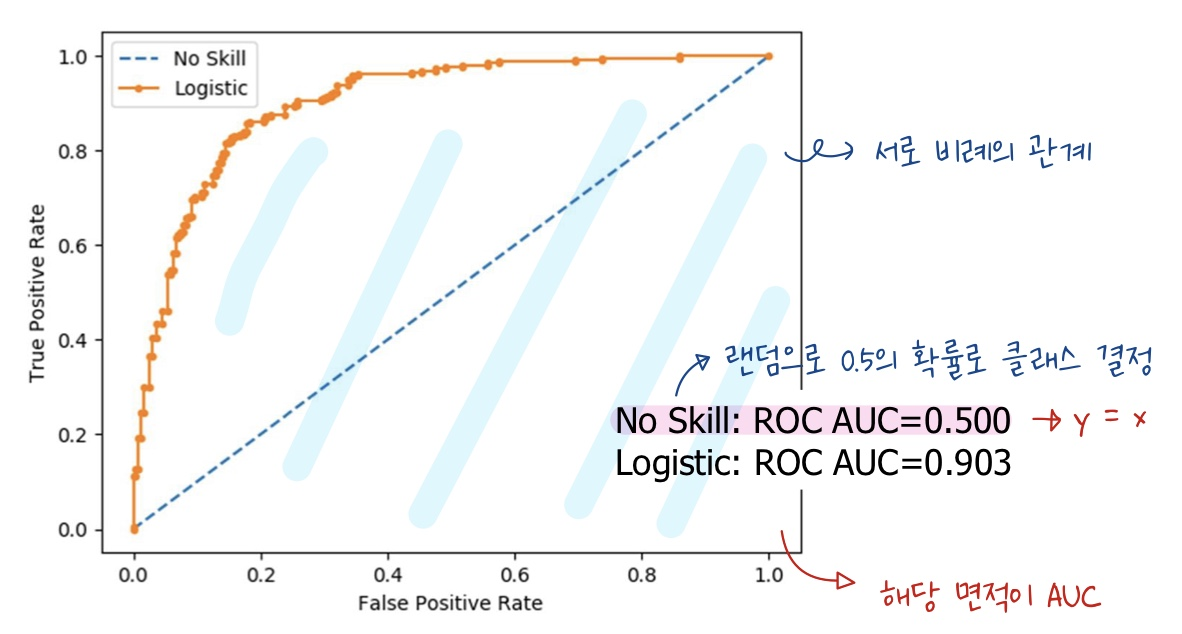
-
두 부류에 포함되어지는 데이터 개수가 비교적 비슷하다면 ROC 곡선을 이용하여 성능을 판단한다.
-
X 축은 거짓 긍정률을 의미하고 Y 축은 참 긍정률을 의미한다
-
AUC란 곡선 아래의 면적을 의미한다. 해당 면적이 1에 가까울 수록 성능이 높아진다.
⚡ Precision-Recall 곡선
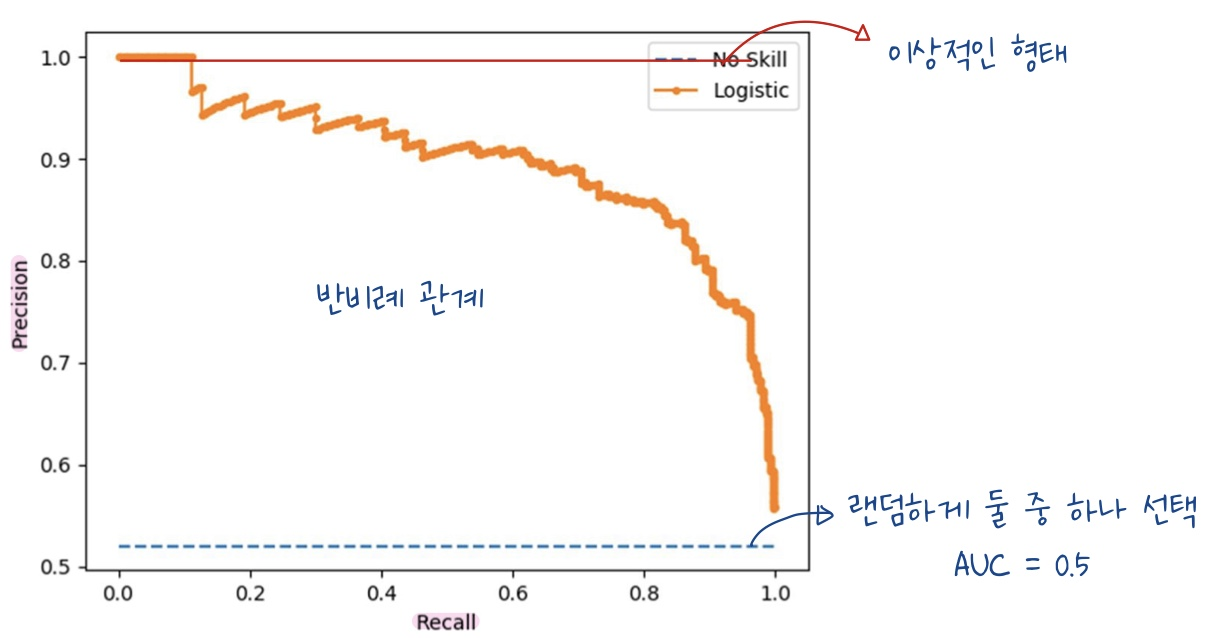
-
두 부류에 포함되어지는 데이터 개수가 비교적 균등하지 않을 때 Precision-Recall 곡선을 사용한다.
-
Precision-Recall 곡선의 경우에는 x축의 값이 재현율이고 y축의 값이 정밀도를 의미한다.
-
두가지 사이의 상관관계는 서로 반비례 형태를 가지게 된다.
-
해당 곡선 또한 AUC의 값이 1에 가까워 질 수록 높은 성능을 가진다고 말 할 수 있다.