DFS & BFS

✅ 탐색(Search)

• 여러 데이터 중에서 원하는 데이터를 찾는 과정

  탐색 알고리즘

  • DFS, BFS

▶ 재귀함수

자기 자신을 다시 호출하는 함수

• 언제 끝날지, 종료 조건을 반드시 명시 ➡ 무한 호출 방지

• 재귀 함수의 수행은 스택 자료구조를 이용 ➡ 마지막에 호출한 함수가 먼저 수행을 끝내야 앞의 함수 호출이 종료

💨 그래프 표현 방식

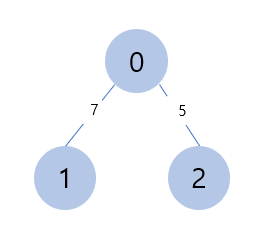
인접행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식

INF = 9999999999 # 무한의 비용

gragh = {
	[0, 7, 5],
    	[7, 0, INF],
    	[5, INF, 0] }

• 모든 관계를 저장 ➡ 노드 개수가 많을수록 메모리가 불필요하게 낭비

인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식

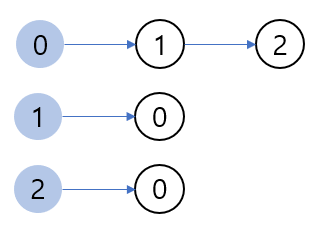
graph = [[] for _ in range(3)]

graph[0].append((1, 7))
graph[0].append((2, 5))

graph[1].append((0, 7))

graph[2].append((0, 5))

• 연결된 정보만을 저장 ➡ 메모리를 효율적으로 사용

✅ DFS

• 깊이 우선 탐색 ➡ 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘

• 특정한 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘

• 재귀 함수를 사용

  • 📌 탐색 과정

  1. 탐색 시작 노드를 스택에 삽입하고 방문 처리

  2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼내기.

  3. 2번의 과정을 더 이상 수행 할 수 없을 때까지 반복

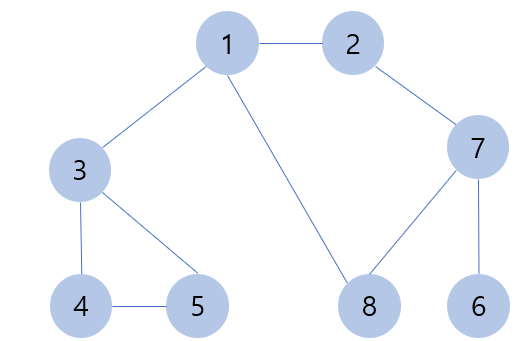
def dfs(graph, v, visited):
	#현재 노드를 방문 처리
    visited[v] = True
    
    for i in graph[v]:
    	if not visited[i]:
        	dfs(graph, i, visited)
            
graph = [
     [],
     [2, 3, 8],
     [1, 7],
     [1, 4, 5],
     [3, 5],
     [3, 4],
     [7],
     [2, 6, 8],
     [1, 7]
]

visited = [False] * 9

dfs(graph, 1, visited)

✅ BFS

• 너비 우선 탐색 ➡ 가까운 노드부터 탐색하는 알고리즘

• 큐 자료구조를 사용하는 것이 일반적

  • 📌 탐색 과정

  1. 탐색 시작 노드를 큐에 삽입하고 방문 처리

  2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리

  3. 2번의 과정을 더 이상 수행 할 수 없을 때까지 반복

def bfs(graph, v, visited):
	#현재 노드를 방문 처리
    queue = deque([start])
    
    visited[start] = True
    
    while queue:
    	v = queue.popleft()
        
        for i in graph[v]:
        	if not visited[i]:
            	queue.append(i)
                visited[i] = True
            
graph = [
     [],
     [2, 3, 8],
     [1, 7],
     [1, 4, 5],
     [3, 5],
     [3, 4],
     [7],
     [2, 6, 8],
     [1, 7]
]

visited = [False] * 9

dfs(graph, 1, visited)