Transformer

Attention Mechanism

Attention이란, sequence 내에서, 두 토큰이 얼마나 강하게 연관되는지 판단할 수 있도록 연산 통로를 만들어주면 모델이 학습을 통해 서로의 연관관계를 파악할 수 있게 되는 것입니다. 이 정보를 토대로 현재 타깃 위치의 토큰을 더 잘 encoding할 수 있습니다.

Embedding 직후나, 다른 인코더를 거친 $D$차원의 벡터로 연산을 진행하며, 연산 결과 역시 $D$차원입니다.

이는 본질적으로 어떤 토큰을 encoding할 때, 다른 토큰의 의미를 가중 평균(weighted averaging)해서 이용하는 것입니다.

Self-Attention

Self-Attention은 입력을 Query(q), Key(k), Value(v)로 선형 변환하고 내적 연산을 실행하는 것을 의미합니다. query는 현재 토큰을 의미하고, key는 query와 비교할 토큰입니다. Self-Attention은 query와 key의 유사성을 가중치로 하여 value들의 가중합을 내게 됩니다.

이때, $(W^Q, W^K, W^Z)$는 모델이 학습하면서 최적화하는 weight matrix이고,
$Q, K, V$는 다음과 같이 정의합니다.


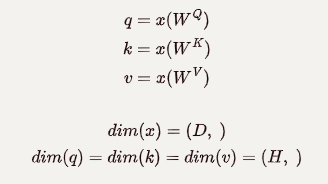
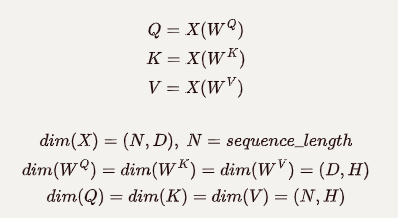
Self Attention 과정을 더욱 자세히 살펴보면 4단계로 나눌 수 있습니다.

1. $N$개의 토큰으로 이루어진 입력 sequence를 $Q, K, V$로 변환. 이때 하나의 토큰은 $D$차원으로 이루어진 벡터이고, 그 토큰에 해당되는 $q, k, v$는 $H$차원의 벡터이다.

2. 각 토큰(query)마다 다른 토큰(key)와 유사성을 비교(내적: 결과는 스칼라)하여 Attention score를 계산한다. query마다 key가 $N$개 있으므로 query 하나에 대한 Attention score는 $N$차원 벡터이고, query가 $N$개 이므로 전체 Attention score는 $N\times N$ 행렬이다. 각 행이 하나의 query에 대한 결과에 대응한다.

3. Attention Score를 key의 차원($d_k$; 이 경우, $H$)의 제곱근으로 나누어 scale한다 (scaling은 attention 결과가 softmax에서 기울기가 0이 아닌 부분에 mapping되도록 하는 역할이다). Softmax를 행별로 적용한다(axis=0). 따라서 각 행마다 요소를 모두 합하면 1이다.

4. 3의 결과($R$)는 $V$에 대한 가중치 행렬로 작용하며 $V$와 행렬곱해$(RV)$, $Z$를 얻는다. 행렬곱은 가중합의 의미이다. $Z$는 $(N, H)$차원이다.

   $Z = softmax(\frac{QK^T}{\sqrt{d_k}})V$

Multi-head Attention

지금까지는 $W^Q, W^K, W^V$가 하나였습니다. Transformer는 여러 쌍의 $(W^Q, W^K, W^V)$를 이용해, 모델이 다른 토큰에 더욱 집중할 수 있게 해 주고, representation을 다채롭게 하는 유용성이 있습니다.

Self-Attention을 거치면 각 쌍의 $(W^Q_i, W^K_i, W^V_i)$ 마다 $(N, H)$ 차원의 결과 $Z_i$ 를 얻습니다. 총 $m$개의 쌍이 있다면, $(Z_1, Z_2, ..., Z_m)$을 concatenate 하여 $(N, mH)$차원의 $Z_{concat} = [Z_1, Z_2, ..., Z_m]$를 생성합니다.

마지막으로 $(mH, D)$차원의 $W^O$를 정의하여 $(N, D)$차원의 output, $Z$를 얻게 됩니다.