Batch Normalization

Batch Normalization은 2015년에 제안된 이래로 꾸준히 쓰이고 있는 정규화 기법입니다.
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

왜 Batch Normalization이 잘 되는지 간략하게 살펴보고 backpropagation에 대해 다루겠습니다.

Motivation

원 논문에서는 Internal Covariate Shift를 막기 위한 제안이라고 밝혔습니다. 그러나 후속 연구에 따르면 Internal Covariate Shift를 막기 때문에 Batch Normalization이 잘 작동하는 것이 아니라고 주장합니다.
참고-1

딥러닝에서 높은 정확도를 얻기 위해서는 안정적인 학습과정을 제공하는 것이 중요합니다. 이는 본질적으로 Loss function landscape가 얼마나 부드러운지(parameter space에서 Gradient 방향으로 한 스텝 나갔을 때, 도착점의 Gradient와 출발점의 Gradient가 비슷한지)가 중요합니다.

Batch Normalization을 거치고 나면 오른쪽처럼 부드러워지게 되어 최적화가 잘 되는 경향이 생깁니다.
참고-2

Algorithm

Normalization이 optimization과 연결되어 있지 않은 경우, optimization에 따른 activation의 변화에도 loss는 변하지 않게 되어 안정적인 학습을 방해합니다.
예를 들어, zero-mean을 만들기 위해 activation에서 평균을 빼는 방식으로 Normalize하게 된다면, 더해지는 bias $b$는 $\Delta b \propto - \partial l/\partial \hat x,\;(\hat x=x-E[x])$인 $\Delta b$만큼 계속 변하게 되지만, layer의 출력인 $\hat x$에는 미치는 영향이 상쇄되기 $(x-E[x] = x + \Delta b -E[x+\Delta b])$ 때문입니다.
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift - 2. Towards Reducing Internal Covariate Shift

위의 문제를 해결하려면 training set전체에 대해 covariance를 구해야 하므로 비용이 많이 들어갑니다.

따라서, mini-batch별로 평균, 분산을 예측하고, dimensionwise하게 normalize하는 Batch Normalization을 사용합니다

1차원 입력 $(shape = (m, 1))$에 대한 적용 예시입니다. 평균과 분산을 구하고, 평균 0, 분산 1인 분포로 만든 후, 학습 가능한 parameter: $\gamma, \beta$를 이용해 변환한 것을 알 수 있습니다.
이때, $\gamma, \beta$의 존재가 $x |\rightarrow y$ 의 변환을 항등변환(identity)으로 만들 수 있다는 것이 중요합니다. 만약 sigmoid의 출력을 정규화(평균 0, 분산 1인 분포로 만드는 것)만 한다면, 그 결과는 모두 sigmoid의 선형성이 강한 영역에 놓일 수 있고, 이는 모델의 표현력을 약화시킵니다. 그러나 $\gamma = Var[x], \beta=E[x]$가 되는 경우 $y=x$가 되고, Batch Normalization은 항등변환을 포함합니다. 따라서 Batch Normalization은 모델의 표현력을 잃지 않습니다.

Backpropagation

Understanding the backward pass through Batch Normalization Layer을 참고하여 작성하였습니다.

입력단에 가까운 쪽을 아래, 출력단에 가까운 쪽을 위라고 표기하였으며, loss function $l$, 변수 $z$에 대하여 $dz \equiv \frac{\partial {l}}{\partial{z}}$로 정의했습니다.
$x$를 $N$행 $D$열 행렬로 표기하고 그때의 차원을 $(N, D)$라고 표기하였으며,
$\gamma, \beta$는 $D$차원 행벡터이고, $(D,)$로 차원을 표기합니다.

Feedforward pass는 다음과 같습니다.

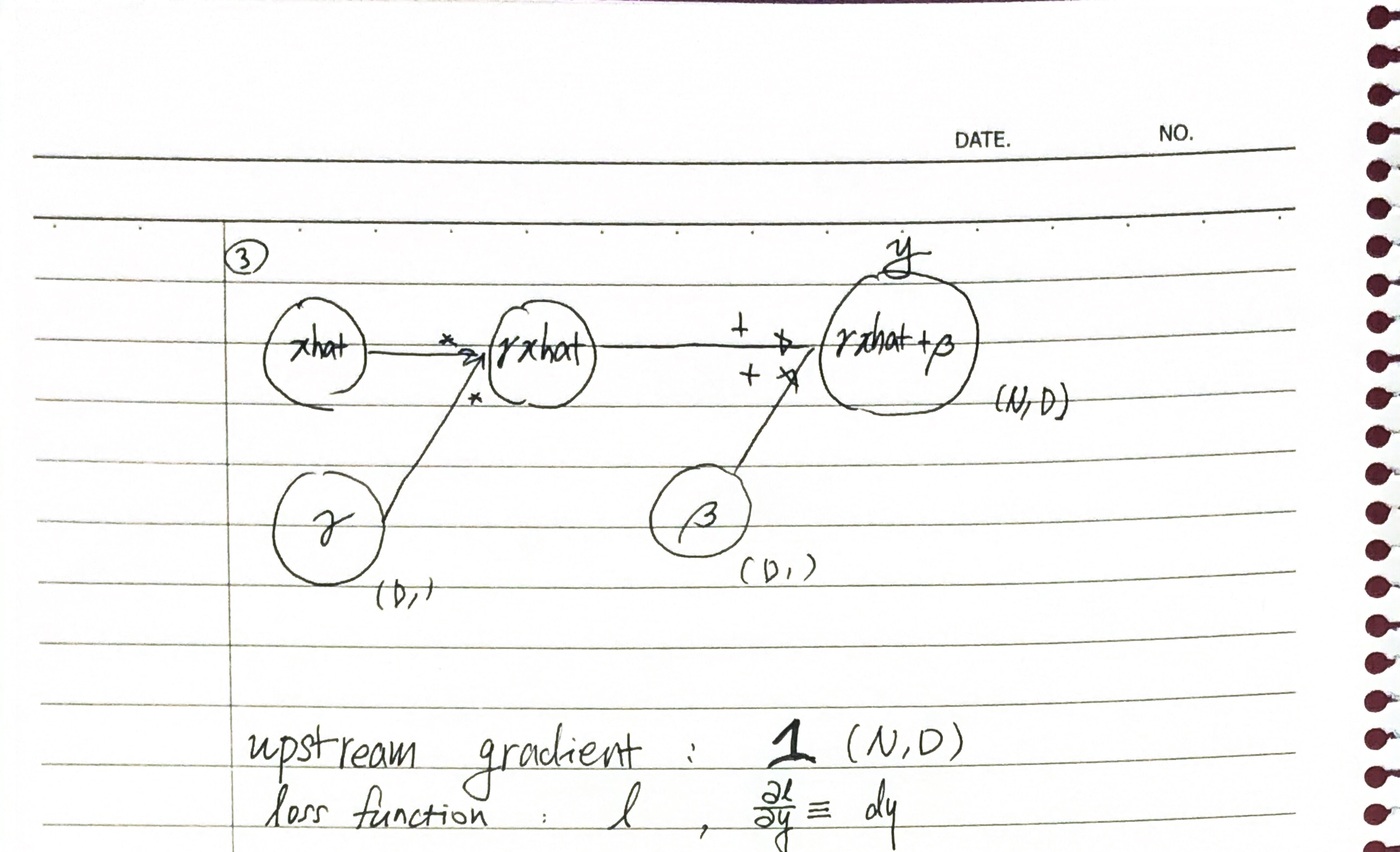
이에 따라 backward pass 역시 구해 봅니다. 동그라미에 해당하는 변수가 $z$라면 동그라미와 연결된 오른쪽 선이 $dz$를 의미합니다.
Chain rule에 의해 $d(아래) = d(위) *\frac{\partial 위}{\partial아래}$ 로 표기할 수 있습니다.

(feedforward에서 batch에 대해 평균을 내는 연산의 backpropagation - 1)

(feedforward에서 batch에 대해 평균을 내는 연산의 backpropagation - 2)

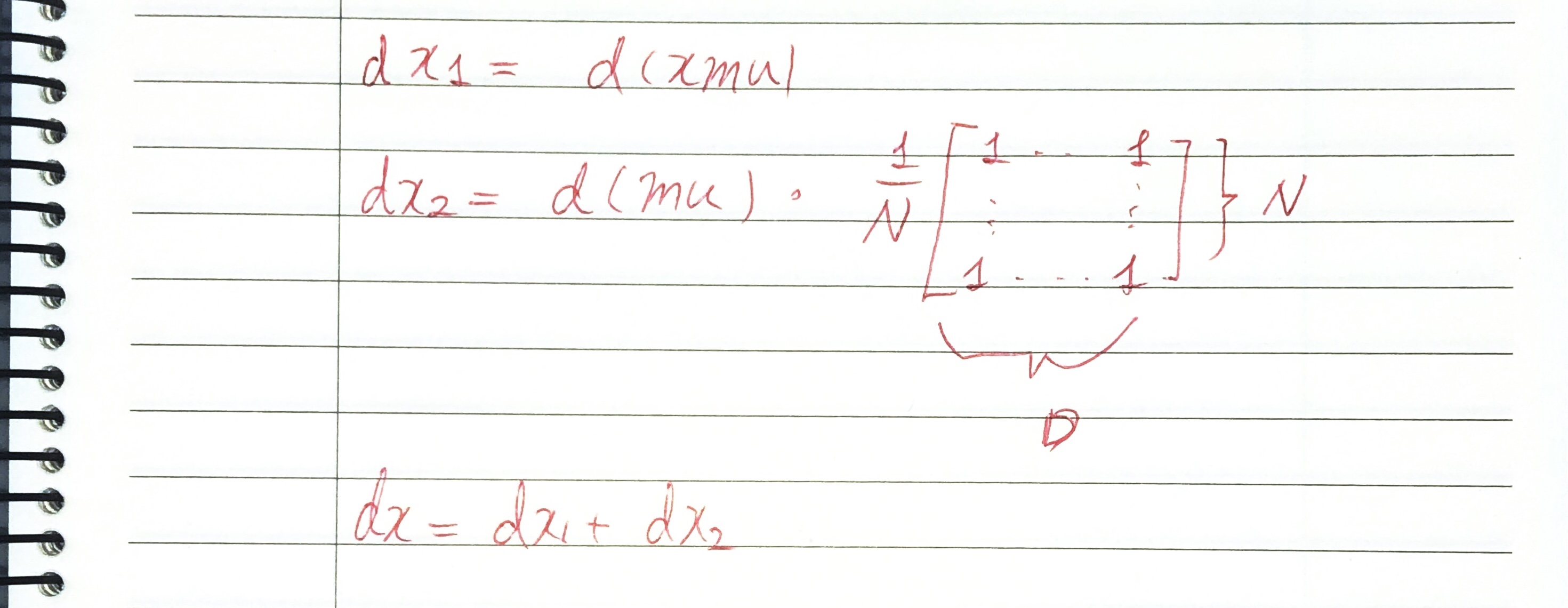
$dx, d\gamma, d\beta$를 모두 구하였습니다. 따라서 Batch Normalization의 backpropagation이 마무리되었습니다.

추가

Feedforward과정에서 batch에 대해 평균$(\frac 1 N\sum_i^N)$을 내는 과정은 backward pass에서 모든 성분이 $\frac 1 N$인 $(N,D)$ 행렬을 곱하였는데 그 이유는 다음과 같습니다.

반대로, feedforward에서 $D$차원 행벡터가 $(N,D)$행렬로 broadcasting되는 경우 batch에 대한 덧셈$(\sum_i^N)$으로 처리됩니다.