Backpropagation, 벡터로 미분하기

Gradient Descent 방법에서 backpropagation이나 가중치 업데이트 등의 토픽을 다루다보면
Loss function을 가중치로 미분하는 연산이 등장합니다. 이때, 가중치는 행렬이므로 스칼라 함수를 행렬로 미분하는 연산을 정의해야 합니다.

1. Notation

스칼라는 $x, y, c$ 등의 소문자로, 열벡터$(n \times 1)$는 $\bf a$, $\bf b$ 등의 볼드체 소문자로, 행렬은 $A, B$ 등 대문자로 표기하겠습니다. 따라서 행벡터$(1 \times n)$은 $\bf a^T$, $\bf b^T$가 됩니다.
벡터의 크기는 $\bf a^T a$, 내적은 $\bf a^T b$ 등으로 표현할 수 있습니다. 예외적으로 Loss function의 경우 스칼라지만 대문자 $L$로 표기하겠습니다

2. Numerator layout vs Denominator layout

위키피디아 링크
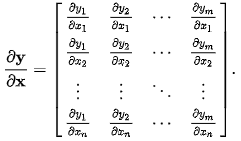
$\bf y$ $(m \times 1)$를 $\bf x$ $(n \times 1)$로 미분한 결과의 차원이 $(n\times m)$이 되는 표기법과 $(m\times n)$이 되는 표기법이 공존합니다.

분자중심표기(Numerator layout): $\frac{\partial \bf y}{\partial \bf x}$는 $(m\times n)$ 행렬이 됩니다. 즉, 행의 개수가 분자와 같습니다.

분모중심표기(Denominator layout): $\frac{\partial \bf y}{\partial \bf x}$는 $(n\times m)$ 행렬이 됩니다. 즉, 행의 개수가 분모와 같습니다.

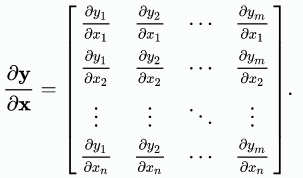
식을 보면 $\bf x$는 원래의 형태인 열벡터처럼 행을 따라 $x_1, x_2, x_3, ... x_n$으로 나열되어 있고, $\bf y$는 원래의 형태가 아닌 그 트랜스포즈처럼 열을 따라 $y_1, y_2, y_3 ..., y_m$으로 나열됩니다. 즉 분모는 원래의 모양대로 나열되고, 분자는 트랜즈포즈로 나열됩니다.
이 포스트에서는 분모중심표기를 따르겠습니다. SGD는 가중치를 $W \rightarrow W -\alpha\nabla_W L$에 따라 업데이트하는데 $\nabla_W L$이 곧 $\frac{\partial L}{\partial W}$이고, $W$와 연산이 가능하려면 같은 모양이어야 하기 때문입니다.

3. Cross Entropy Loss 를 Weight로 미분하기

이제부터는 직접 예시를 통해 벡터에 대한 미분과 행렬에 대한 미분을 살펴봅니다.

$L$이 Loss function (스칼라)이고 W는 가중치 행렬일 때, $\frac{\partial L}{\partial W}$는 분모인 $W$의 모양대로 나열됩니다.
입력 노드가 4개이고, 출력 노드가 3개인 1-layer Perceptron 을 생각해보겠습니다.

이 모델으로 분류 문제를 풀도록 합니다.

이 때, activation으로는 softmax를 사용하고, Loss function은 cross entropy를 사용합니다.
$W$는 $(4\times 3)$의 행렬이고, 입력 ${\bf{x^T}}$는 np.array([[0.2, -0.4, 0.3, 0.5]])를 사용해 봅니다.

${\bf{x^T}}$에 대해서 살펴본다면 batch_size를 $N$, 차원을 $D$라고 할 때 $(N\times D)$ 모양입니다. $N=1$이고, 행벡터 형태로 사용하기 때문에 트랜스포즈로 표기했습니다.

${\bf{x^T}}W$의 모양은 $(1\times 3)$으로 각 행에 대해 softmax를 적용한 뒤에도 $(1\times 3)$이 유지됩니다.
${\bf{z^T}}={\bf{x^T}}W$ 라고 하고, softmax를 $f$라고 하면 적용한 결과는 ${\bf{y^T}}={f(\bf{z^T})}$ 로 표기할 수 있습니다.

chain rule ($\frac{\partial y}{\partial x_i} = \sum_{\ell = 1}^m \frac{\partial y}{\partial u_\ell} \frac{\partial u_\ell}{\partial x_i}$)에 의해,

$\frac{\partial L}{\partial W} = \sum_{i, j}\frac{\partial L}{\partial \bf{y^T_i}} * \frac{\partial \bf{y^T_i}}{\partial \bf{z^T_j}}* \frac{\partial \bf{z^T_j}}{\partial W}$ 입니다.

1. $\frac{\partial L}{\partial \bf{y^T}}$ 구하기(스칼라를 벡터로 미분)

벡터 미분에 앞서, Loss function을 $\bf{y^T}$의 각 component로 미분한다면 어떻게 될 지 살펴봅시다.
label이 one-hot encoded vector라고 한다면 Cross Entropy Loss 는 다음과 같습니다.

# calculate cross entropy
def cross_entropy(p, q):
	return -sum([p[i]*log(q[i]) for i in range(len(p))])

ce = cross_entropy(expected, predicted)
loss = mean(ce, axis=0)

${p}$는 label이고 ${q}$는 예측값입니다.
이 때 label은 one-hot encoded vector입니다. 따라서 단 하나의 index에 대해서만 그 값이 1이고, 나머지는 0이 됩니다.

$\frac{\partial L}{\partial q_i}=-\frac{1}{N}\frac{p_i}{q_i}$

$N=1$이고, $j$가 정답 인덱스라고 한다면,

$\frac{\partial L}{\partial q_i}= 0(i\neq j) \;or -\frac{1}{q_j}(i=j)$ 입니다.

$L$은 스칼라이고 , $\bf{y^T}$는 벡터이므로 $\frac{\partial L}{\partial \bf{y^T}}$는 $\bf{y^T}$와 그 형태가 같고, 그 값들은 $L$을 $\bf{y^T}$의 각 성분으로 미분한 것과 같습니다. 예측값 $\bf{y^T}$를 y_pred로 저장하고 $\frac{\partial L}{\partial \bf{y^T}}$를 y_pred_grad의 변수에 넣는다면 다음과 같습니다.

label = np.array([[0, 1, 0]])
y_pred = np.array([[0.3, 0.4, 0.3]])

y_pred_grad = np.where(label==1, -1.0/y_pred, 0)

print(y_pred_grad)
# np.array([[0, -2.5, 0]])

2. $\frac{\partial \bf{y^T}}{\partial \bf{z^T}}$ 구하기(벡터를 벡터로 미분)

$(1\times 3)$벡터를 $(1\times 3)$벡터로 미분하는 것이니 그 형태가 $(3\times 3)$이 될 것을 알 수 있습니다.
$\bf{y^T}$의 각 성분을 $y_1, y_2, y_3$, $\bf{z^T}$의 각 성분을 $z_1, z_2, z_3$라 하면 $\frac{\partial \bf{y^T}}{\partial \bf{z^T}}_{ij} = \frac{\partial {y_j}}{\partial {z_i}}$입니다.

$y_i =\frac{e^{z_i}}{\sum_j {e^{z_j}}}$이므로 미분하면,

이 됩니다.

3. $\frac{\partial \bf{z^T}}{\partial W}$ 구하기(벡터를 행렬로 미분)

$\bf{z^T} = \bf{x^T}$ $W$에서
$\frac{\partial \bf{z^T}}{\partial W}$를 $\bf{x^T}$ 로 쓰고 싶을 수 있습니다. 그래도 되는지 살펴보겠습니다.

wikipedia에서 Matrix Calculus를 살펴보면 벡터를 행렬로 미분하는 경우는 굉장히 드물고, 잘 정의되지 않는다고 합니다.

따라서, $\bf x$ 와 $\bf x^T$ 중 어느 쪽이 맞는지 비교해보고 넘어가겠습니다.
1, 2에서 얻은 결과

를 통해,
$\frac{\partial L}{\partial \bf{z^T}}=[y_1\quad y_2 -1\quad y_3]$임을 알 수 있고, 간단히 y_pred - label로 계산할 수 있게 됩니다.

$\frac{\partial L}{\partial W}=\frac{\partial \bf{z^T}}{\partial W}\frac{\partial L}{\partial \bf{z^T}}$에서 분모중심표기에 따라 차원을 비교하면,
$(4\times 3) =(4 \times N) * (N \times 3)$이 되어야 한다는 것을 알 수 있고,
따라서 $\frac{\partial \bf{z^T}}{\partial W} = \bf{x}$ 입니다.

결론

1-layer perceptron에서 입력이 $\bf x^T$이고 softmax layer를 통과한 출력이 $\bf y^T$, label이 $\bf y_{true}^T$이고 Loss function이 Cross Entropy일 때,

$\frac{\partial L}{\partial W}=\bf{x}$$[y_1\quad y_2 -1\quad y_3]\\\quad =\bf{x}$ $\frac{1}{N}(\bf{y^T}-\bf{y_{true}^T})$입니다.
이 때, $\bf{x}$는 입력$\bf{x^T}$ $(N\times D)$의 트랜스포즈이므로 $(D\times N)$입니다

참고

https://atmos.washington.edu/~dennis/MatrixCalculus.pdf

밑바닥부터 시작하는 딥러닝 3