Backpropagation이란?

Gradient Descent 방법을 사용할 때 필수적인 알고리즘으로서, Weight Matrix $W$를 Cost Function $C$가 가장 작게 하는 업데이트 $W \rightarrow W - \alpha \frac{\partial {C}}{\partial {W}}$ 를 실시할 때, $\frac{\partial {C}}{\partial {W}}$를 빠르게 계산하는 방법입니다. Weight를 하나씩 변화해가며 gradient를 계산하는 방법에 비해 한꺼번에 모든 Weight의 gradient를 계산하여 연산 속도를 비약적으로 상승시켜 딥러닝의 핵심적인 기법이 되었습니다.

다층 퍼셉트론(Multi-Layer Perceptron)에 대한 Backpropagation을 유도와 함께 설명하겠습니다.

이 글은 CHAPTER 2 How the backpropagation algorithm works을 따라 정리한 글입니다.

Warm up

유도에 쓰이는 연산을 정리합니다

Chain rule

$y = f(u_1, u_2, ..., u_m),\quad u_i = g_i(x)$ 일 때, $\frac{\partial {y}}{\partial {x}} = \sum_{i=1}^m \frac{\partial {y}}{\partial {u_i}}\frac{\partial {u_i}}{\partial {x}}$ 가 성립합니다. 이를 chain rule이라고 합니다.

Matrix-Vector multiplication

$y_j =\sum_k M_{jk} x_k$ 일 때, ${\bf{y}} =M{\bf{x}}$ 라고 씁니다. ${\bf{x}}$가 $(n, 1)$벡터, $M$이 $(m,n)$행렬일 때, ${\bf{y}}$는 $(m,1)$벡터가 됩니다. 즉, 차원을 비교하면 $(m,1) \leftarrow (m, n)\times(n,1)$입니다.

Hadamard product - ⊙

차원이 같은 벡터 둘 사이에서 정의된 연산으로 연산 결과 역시 차원이 같은 벡터이며, 각 성분은 원래의 두 벡터에서 위치가 같은 두 성분의 곱입니다. 따라서, 어떤 벡터의 각 성분이 다른 두 벡터의 성분별 곱과 같다면($p_j = s_jt_j$), Hadamard product를 사용하여 $p\;=s\; ⊙\;t$로 표기할 수 있습니다.

Applying function to vectors

$y$가 벡터일 때, $q = f(y)$라는 표기는 $q_j = f(y_j)$을 의미합니다. 즉 함수를 벡터에 작용하면, 각 성분에 함수를 적용한 결과를 각 성분으로 갖는 벡터가 됩니다.

Notation

MLP에서 각 layer에서 가중합에 activation을 적용하여 다음 layer로 전달합니다. 이에 대한 backpropagation을 유도하기 전에 표기법을 정하고 시작해야 합니다.

• Loss function은 $C$, activation은 $\sigma$로 표기합니다.
• $l$번째 layer의 $j$번째 Node로의 입력 중, $l-1$번째 layer의 $k$번째 Node로부터 온 것은 $w_{jk}^l a_k^{l-1}$으로 표기합니다. 즉, subscript는 도착 Node, 출발 Node 순으로 적고, superscript는 도착 layer를 적습니다.
• activation을 적용하기 전의 값은 $z$로 표기합니다.
• 벡터 $a^l$의 각 성분 $a^l_j$은 $a^l_j=\sigma(z_j^l)$을 만족하므로, $\quad a^l=\sigma(z^l)$로 표기할 수 있습니다.

BP equations

이제 준비가 끝났습니다. MLP에서의 backpropagation은 4개의 방정식으로 정리되는데, 하나씩 유도해 보겠습니다. 각 방정식의 의미에 대해서는 CHAPTER 2 How the backpropagation algorithm works를 참고해 주세요.

δ 정의하기

식을 정리하다보면 자주 나오게 되는 $\frac{\partial {C}}{\partial {z_j^l}}$를 간단하게 $\delta_j^l$로 표기합니다.

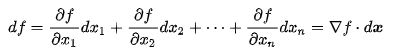
위 식에 따르면, $\frac{\partial {C}}{\partial {z_j^l}}$은 $dz_j^l$에 곱해져서 $dC$에 기여합니다. 따라서, 같은 $dz_j^l$의 크기라도 $\frac{\partial {C}}{\partial {z_j^l}}$가 크면 $dC$에 기여하는 것이 큽니다. 이는 $\frac{\partial {C}}{\partial {z_j^l}}$를 $C$가 $z_j^l$의 변화에 대해 민감한 정도로 이해할 수 있다는 의미입니다.

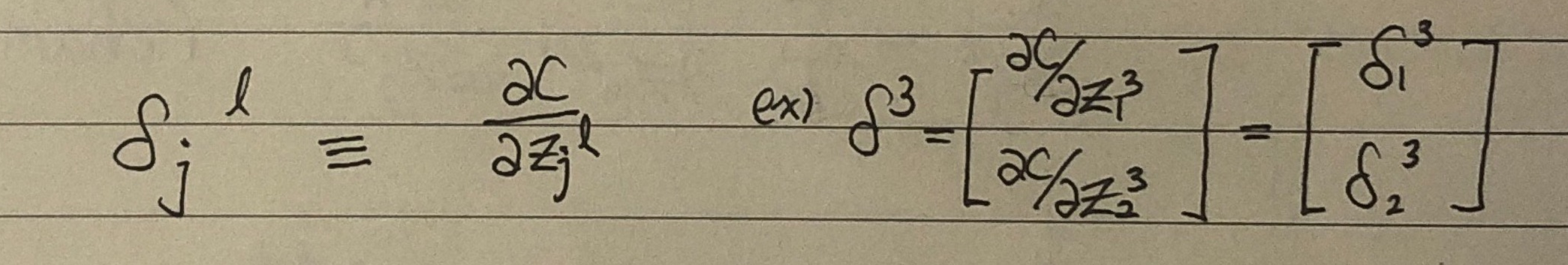
BP1

$δ^L_j=\frac{∂C}{∂{a^L_j}}\;σ′(z^L_j)$ 유도하기

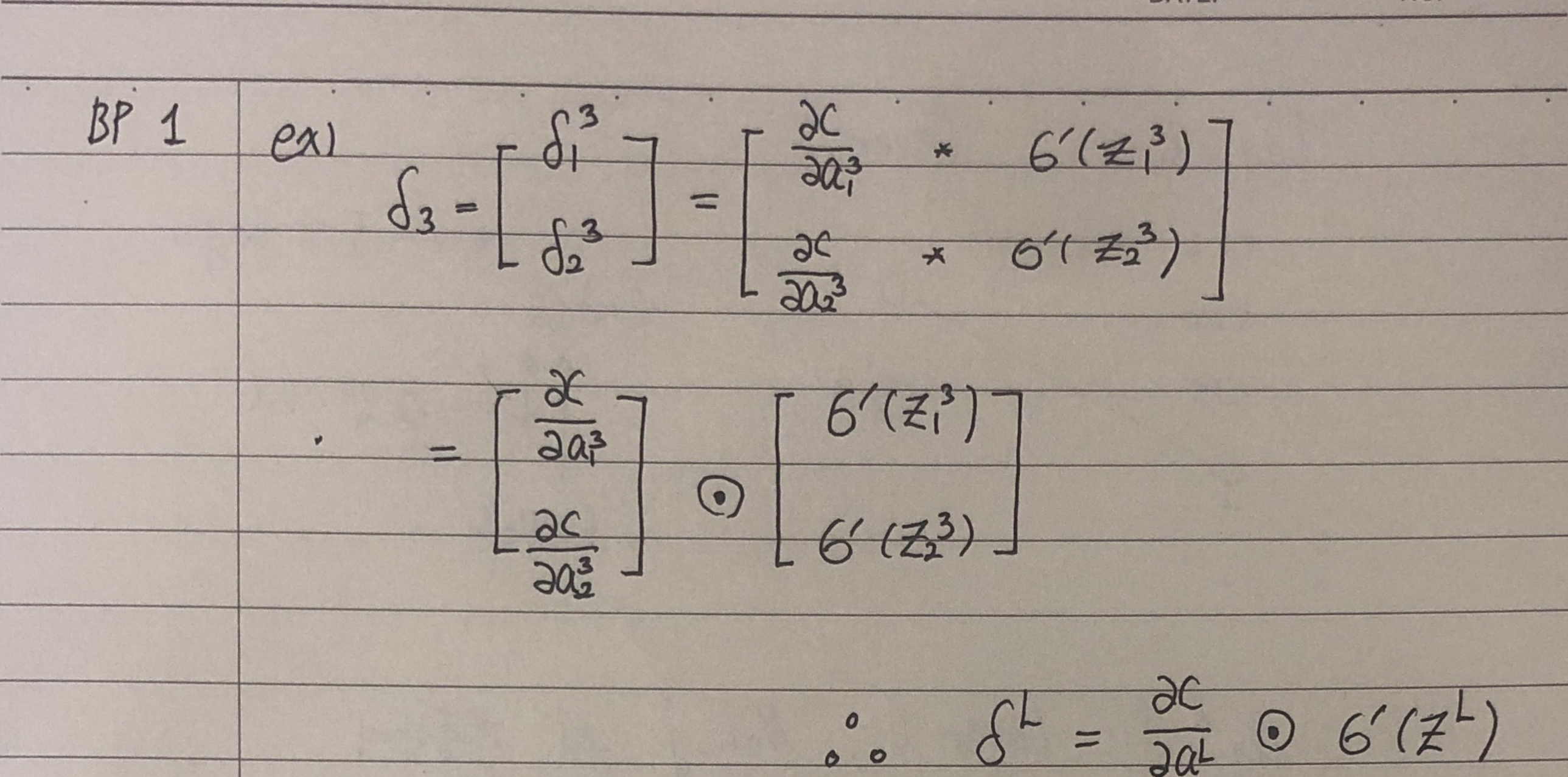
• $δ^L_j$를 계산하기 쉬운 형태로 바꾸어주는 식입니다. Loss function은 최종 출력 $a^L$에 의존하므로 편도함수를 구할 수 있고, $z^L$은 feedforward 단계에서 이미 계산한 값입니다. 또한, $σ′$(activation의 도함수) 역시 알고 있는 형태이기 때문입니다.

BP2

$δ^l=((w^{l+1})^Tδ^{l+1})⊙σ′(z^l)$ 유도하기

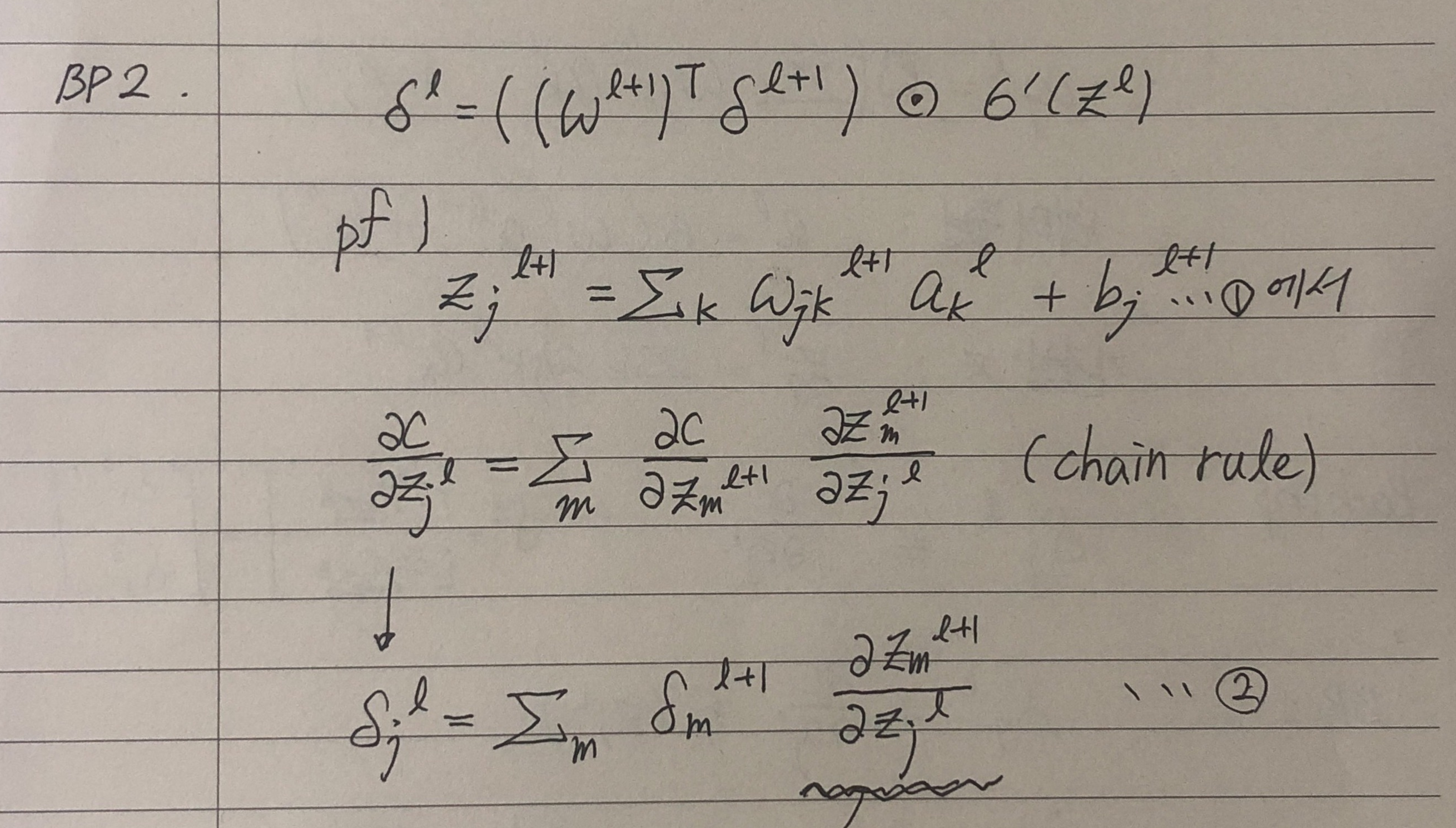
• chain rule과 $\delta$의 정의를 활용하면 식 2까지 진행할 수 있습니다.

• 이 때, 밑줄 친 부분을 어떻게 정리할 지 살펴봅시다.

• $z^{l+1}_m$을 $l$번째 layer로부터의 가중합으로 분해합니다.

• $a_p^l$은 $p\neq j$ 인 경우, $z_j^l$과 무관(편미분하면 0)입니다.

• 따라서 첫째 줄에서 $k=j$인 항만 0이 아닌 값을 갖습니다.

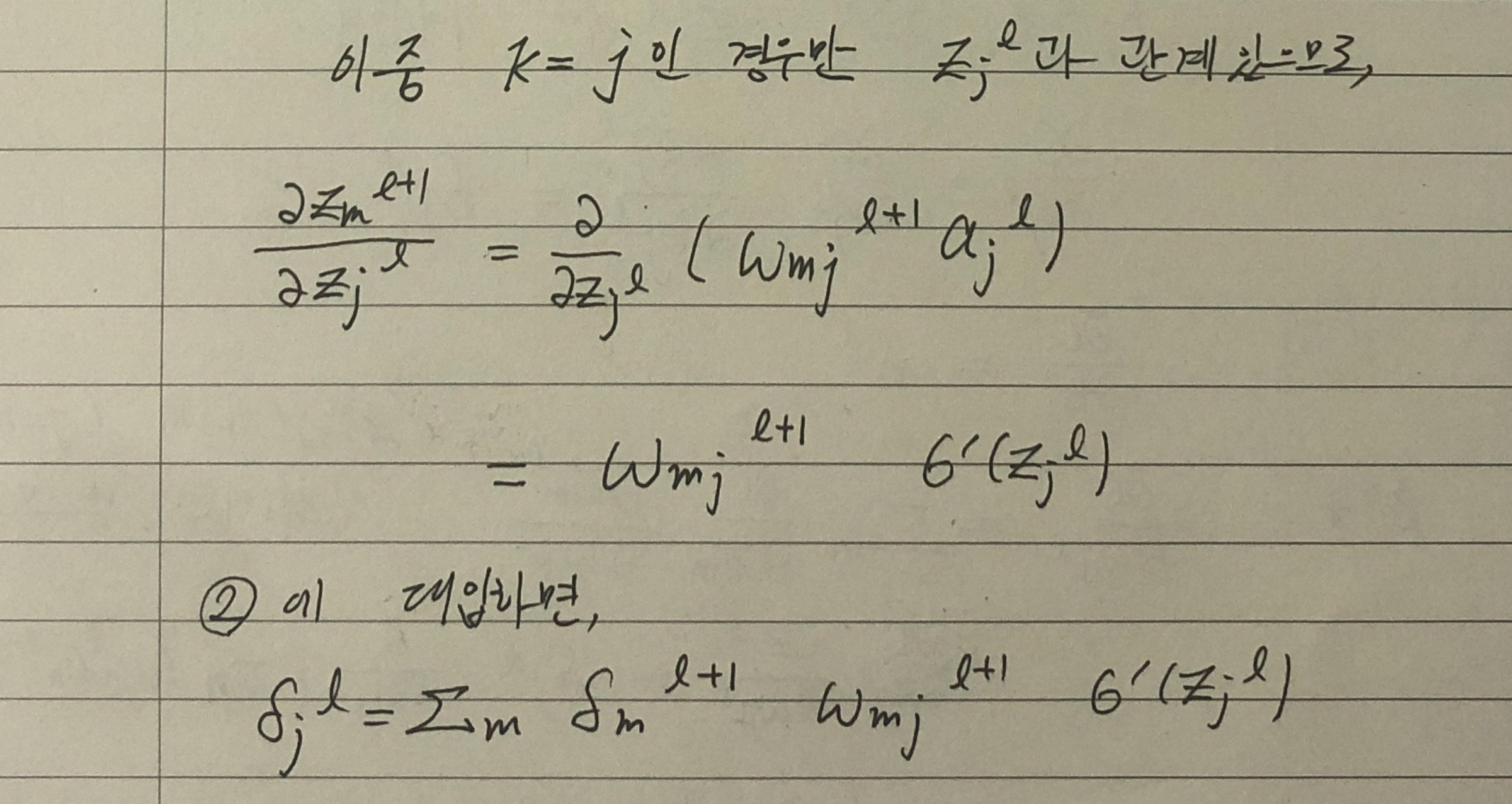
• 이제 마지막 줄을 정리해야 합니다.

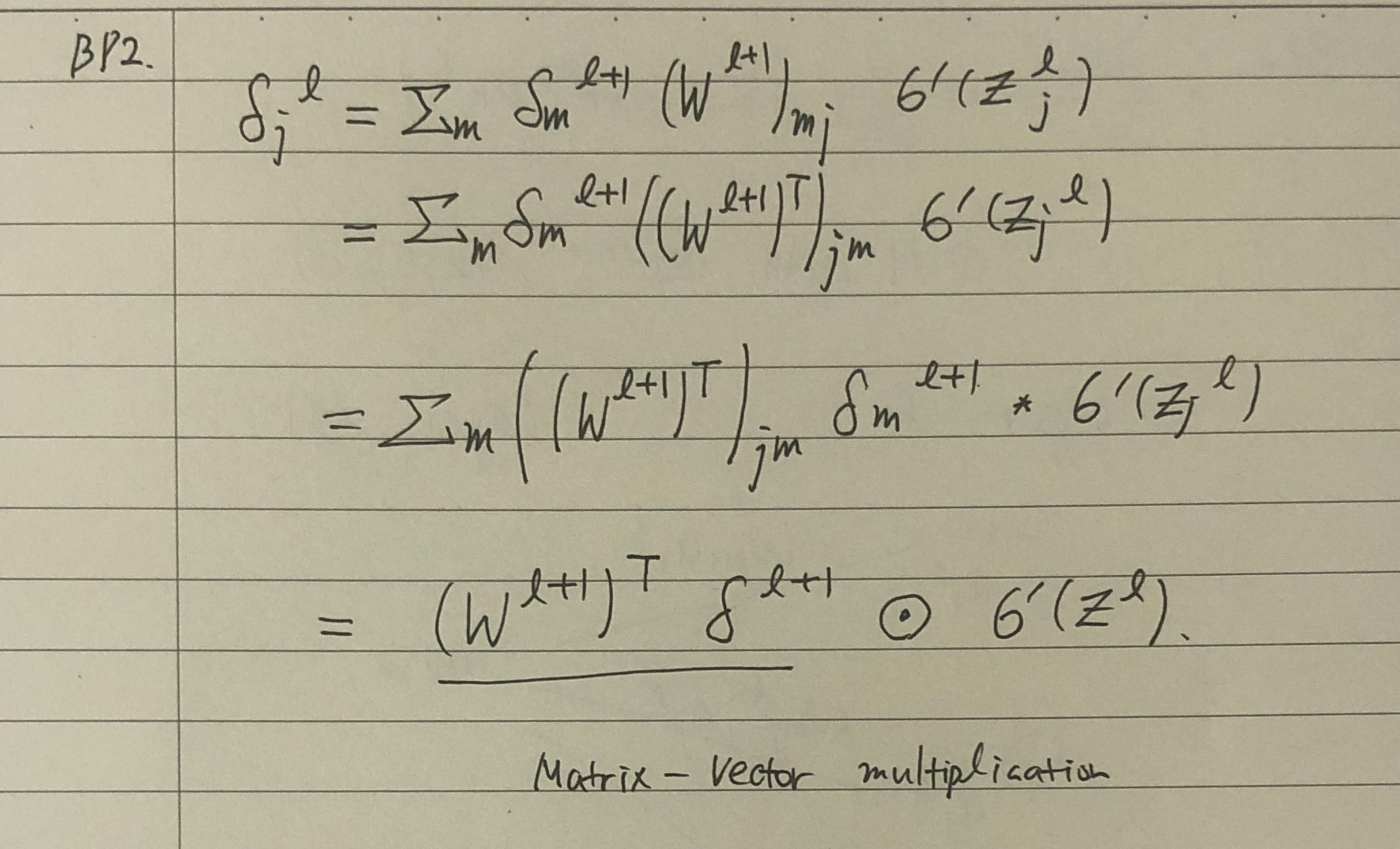
• 행렬$A$의 $(i, j)$ 성분은 $A_{ij}$라고 씁니다. 또는 행과 열을 바꾼 $A$의 transpose: $A^T$의 $(j, i)$ 성분으로 쓸 수 있습니다.

• $w^{l+1}$에 대해서 같은 처리를 하고 나면, summation을 Matrix-Vector multiplication 형태로 바꿀 수 있습니다.

• 결과는 두 벡터의 같은 성분의 곱을 성분으로 갖는 벡터로, Hadamard product로 표기합니다.

BP3, BP4

$\frac{∂C}{∂b^l_j}=δ^l_j,\quad \frac{∂C}{∂w^l_{jk}}=a^{l−1}_kδ^l_j$ 유도하기

• BP4에서, $z^l$의 성분 중, $w^l_{jk}$에 영향을 받는 성분은 $z^l_j$뿐입니다.

• $w^l_{jk}$에서 $j$는 도착 Node를 의미합니다. 다르게 말하면, 직전 layer의 $k$번째 Node에서 $l$번째 layer의 $j$번째 Node로의 연결에만 관여하므로 $l$번째 layer의 다른 Node에는 무관합니다.

• 따라서, $z^l_j$에 관한 항만 살아남게 되고, 두번째 줄로 넘어갑니다.

• $z^l_j$을 가중합으로 분해하고,$n\neq k$의 경우 편미분하면 0이므로, $n=k$ 인 경우에 대해서만 편미분하면 결론을 얻습니다.

• 미분 결과의 형태에 대해서는 Backpropagation, 벡터로 미분하기를 참고해주세요