나머지(Modulo) 연산 분배법칙

알고리즘 문제를 푸는 과정에서 결과 값이 매우 큰 경우, 결과 값의 나머지를 구하라는 문제가 자주 등장한다.
단순히 결과 값에 모듈러 연산을 수행할 시 이미 결과 값은 너무 커져서 오버플로우가 발생한 경우가 대부분이기 때문에, 연산 과정 도중에 모듈러 연산을 적용해야 한다.

연산 과정 도중에 모듈러 연산을 적용하려면 모듈러 연산의 분배법칙에 대해 알아야 한다. 각 피연산자에 모듈러 연산을 취한 후, 계산 결과에 대해 다시한번 모듈러 연산을 취하면 된다. 또한, 뺄셈의 경우 음수가 나오는 것을 방지하기 위해 divisor를 한번 더해준다.

(A + B) % p = ((A % p) + (B % p)) % p
(A * B) % p = ((A % p) * (B % p)) % p
(A - B) % p = ((A % p) - (B % p) + p) % p

마지막으로 나눗셈에 대한 나머지 연산은 분배법칙을 적용할 수 없다. 이는 페르마의 소정리를 이용하여 나눗셈을 곱셉의 형태로 바꾸어줌으로써 해결 가능하다.

페르마의 소정리란, p가 소수이고 a가 정수일때, 다음을 만족한다는 것이다.
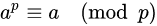이 식의 양변을 a로 나누어주면 다음과 같은 식을 얻을 수 있다.
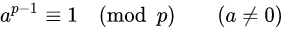여기서 양변을 한번더 a로 나누어 주면 주면 다음처럼 분모에 위치한 수를 분자로 바꿀 수 있다.

즉, 나눗셈에 대한 공식은 다음과 같다.

(A / B) % p = (A * B^(p-2)) % p = ((A % p) * (B^(p-2) % p)) % p