배낭 채우기(Knapsack Problem)

담을 수 있는 무게의 제한이 W인 가방에 물건들을 담는다.
각 물건의 무게와 가치가 주어질 때, 가방에 담을 수 있는 물건들의 가치의 최대합을 구하라

알고리즘 문제를 해결하다보면 위와 같은 문제를 접할 수 있고, 이러한 문제들을 Knapsack Problem이라 한다. Knapsack Problem 중에서도 가방에 넣을 물건을 자를 수 없다고 가정하는 문제를 0-1 Knapsack Problem이라 하는데, 이것을 해결할 수 있는 알고리즘을 구현하겠다.

이 문제는 Dynamic Programing으로 풀 수 있으며, 문제를 풀기 위한 점화식은 다음과 같다.

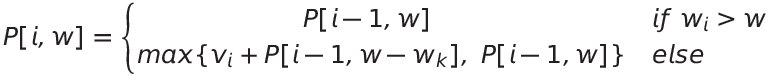
P[i, w]란 i개의 물건이 있고 배낭의 무게 한도가 w일 때, 배낭에 넣을 수 있는 최대의 가치를 뜻한다. 위 점화식은 다음과 같이 해석할 수 있다.

• i번째 물건이 배낭의 무게 한도보다 무거우면 넣을 수 없기 때문에, i번째 물건을 뺀 i - 1개의 물건을 가지고 구한 최대값을 넣어준다.
• 그렇지 않은 경우, i번째 물건을 넣은 경우와 넣지 않은 경우 두가지 경우로 나눌 수 있다.
  - i번째 물건을 넣은 경우는 i번째 무게만큼을 비웠을 때의 최대 값에 i번째 물건의 가치를 더해주면 된다.
  • i번째 물건을 넣지 않은 경우는 i번째 물건을 뺀 i - 1개의 물건을 가지고 구한 최대값이 된다.
  • 위 두가지 경우 중 최대값을 넣어주면 된다.

P[i, w]가 i개의 물건이 있고 배낭의 무게 한도가 w일 때 최대의 가치를 뜻하기때문에, i가 0이거나 w가 0인 경우는 항상 0이 된다는 점을 알고 있어야 한다.

구현 코드

해당 구현 코드는 백준 문제 평범한 배낭을 해결하는 코드이다.

/* 
    배낭 채우기 문제를 해결하기 위한 알고리즘
    배낭에 넣을 수 있는 물건을 자를 수 없는 0-1 Knapsack을 해결.
*/
#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>

#define ITEM_COUNT 100
#define MAX_WEIGHT 100000

using namespace std;


int n, k;
int value[ITEM_COUNT + 1][MAX_WEIGHT + 1]; // DP 배열
int thing[ITEM_COUNT + 1][2]; // thing[i][0], thing[i][1] : 각각 i번째 물건의 무게와 가치

// input을 처리하는 함수
void input(){
    cin >> n >> k;
    
    for(int i = 1; i <= n; i++)
        cin >> thing[i][0] >> thing[i][1];
}

// 0-1 Knapsack 알고리즘
// 다음 점화식을 바탕으로 구현됨
// value[i, w] = 
//   if wi > w :  value[i - 1, w]
//   else      :  max{ vi + value[p - 1, w - wk], value[i - 1, w] }
// value[i, w] 란 i개의 물건이 있고 배낭의 무게 한도가 w일 때, 담을 수 있는 최대 가치를 뜻한다.
// i번째 물건이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로, i번째 물건을 뺀 i-1개의 보석을 가지고 구한 최적의 해를 가진다.
// 그렇지 않으면, 'i번째 물건을 넣기 위해 i번째 물건만큼의 무게를 비웠을 때 최적 값에 i번째 물건의 가치를 더한 값'과
//               'i번째 물건을 넣지 않고 i - 1개의 물건을 가지고 구한 최적의 해' 중 더 높은 값을 취한다.
int knapsack(){
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= k; j++){
            int w = thing[i][0];
            int v = thing[i][1];
            
            if (w > j){
                value[i][j] = value[i - 1][j];
            }
            else{
                value[i][j] = max(value[i - 1][j], v + value[i - 1][j - w]);
            }
        }
    }
    
    return value[n][k];
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    
    
    input();
    
    cout << knapsack() << endl;
    
    return 0;
}