이항계수란 n개의 원소에서 k개의 원소를 뽑아내는 경우의 수를 의미하며, 공식은 다음과 같다.
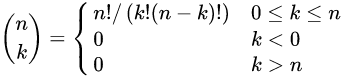위 같은 표현 대신 nCk로 표현하기도 한다.
이항계수를 구하기 위한 알고리즘은 여러 종류가 있는데, 이중 몇가지를 정리하겠다.
Dynamic Programming
Dynamic Programming과 Memoization을 이용하여 이항 계수를 구할 수 있다.
이항 계수와 관련된 공식에는 nCr = n-1Cr + n-1Cr-1 이라는 공식이 있다. 이 공식을 말로 설명하자면, n개의 원소 중 r개를 선택하는 경우의 수은 n-1개의 원소 중 r개를 선택하는 경우의 수와 n-1개의 원소 중 r-1개의 원소를 선택하는 경우의 수의 합이라는 말이다. 더 쉽게 줄여서 말하자면, 하나의 원소를 선택하는 경우의 수 + 하나의 원소를 선택하지 않는 경우의 수이다.
예시를 들어 설명하자면, 1부터 10까지의 자연수(총 10개) 중 4개를 뽑아야한다고 가정하자. 이것을 공식으로 나타내면 10C4이다.
그럼 이제 (A)하나의 원소를 선택하는 경우의 수를 보자. 이것은 1이라는 자연수를 뽑은 뒤 나머지 9개 중에서 3개를 뽑는 경우의 수이며, 9C3으로 나타낼 수 있다.
반대로 (B)하나의 원소를 선택하지 않는 경우의 수는 1이라는 자연수를 뽑지 않은 뒤 나머지 9개 중에서 4개를 뽑는 경우의 수이며, 9C4로 나타낼 수 있다.
1부터 10까지의 자연수 10개 중 4개를 뽑는 모든 경우는 (A) 또는 (B)이다. 또한 (A)와 (B)는 동시에 일어날 수 없다. 그렇기때문에 1부터 10까지의 자연수 10개 중 4개를 뽑는 경우의 수는 (A) + (B)로 나타낼 수 있으며, 공식으로는 10C4 = 9C3 + 9C4로 나타낼 수 있다. 이를 일반환 하면 nCr = n-1Cr + n-1Cr-1이 된다.
위에서 설명한 nCr = n-1Cr + n-1Cr-1의 개념을 가지고 이항계수를 구해보자. 우선 Memoization을 사용하지 않고 재귀함수만을 이용해 코드를 구현해보자.
long long bino_coef(int n, int r){
// r이 n보다 큰 경우의 수는 0이다.
if (r > n)
return 0;
// n개에서 0개를 선택하는 경우의 수와 n개에서 r개를 선택하는 경우의 수는 1이다.
if (r == 0 || r == n)
return 1;
// nCr = n-1Cr + n-1Cr-1
return bino_coef(n - 1, r - 1) + bino_coef(n - 1, r);
}n개의 원소 중 0개를 뽑거나 n개를 뽑는 경우의 수는 1이다. 즉, 재귀 함수의 탈출 조건을 r이 0이거나 n일때로 설정한다. 나머지 경우에 대해서는 nCr = n-1Cr + n-1Cr-1 공식을 이용하여 재귀적으로 접근해준다.
위처럼 코드를 작성할 경우 발생하는 문제는 이미 계산한 부분문제에 대해서도 계속 재귀적으로 호출을 한다는 것이다. 예를 들어 4C2을 보자. 이것을 nCr = n-1Cr + n-1Cr-1 공식을 통해 재귀함수의 탈출 조건이 되는 지점, 즉 r == 0 혹은 r == n일 때까지 나누어보자.
4C2 = 3C2 + 3C1 = 2C2 + 2C1 + 2C1 + 2C0 = 2C2 + 1C1 + 1C0 + 1C1 + 1C0 + 2C0
마지막 식인 2C2 + 1C1 + 1C0 + 1C1 + 1C0 + 2C0을 보면 중복되는 문제들이 보일 것이다. 이 현상은 부분 문제의 양이 늘어날수록 더욱 부각될 것이다.
이를 해결하기 위해 이미 계산한 값에 대해서는 재귀적으로 접근하지 않도록 해야한다. 이 것을 위해 Memoization을 사용한다. 아래 코드는 Memoization을 사용하여 이항 계수를 구한 것이다.
typedef long long ll;
// Dynamic Programing을 이용한 이항 계수 구하기.
// 이항 계수의 방정식 중 하나인 nCr = n-1Cr + n-1Cr-1을 이용한 구현
ll bino_coef_dp(int n, int r){
// Memoization을 위한 배열. static으로 선언하여 값을 유지한다.
static ll dp[100][100] = { 0 };
// r이 n보다 큰 경우의 수는 0이다.
if (r > n)
return 0;
// 이미 계산했다면 바로 값을 반환해준다.
if (dp[n][r] > 0)
return dp[n][r];
// n개에서 0개를 선택하는 경우의 수와 n개에서 r개를 선택하는 경우의 수는 1이다.
if (r == 0 || r == n)
return dp[n][r] = 1;
// nCr = n-1Cr + n-1Cr-1
return dp[n][r] = bino_coef_dp(n - 1, r - 1) + bino_coef_dp(n - 1, r);
}위 코드를 보면 static 2차원 배열인 dp가 선언되어 있는 것을 볼 수 있다. 이 배열에 계산한 값들을 저장해가며, 이미 계산된 결과가 있다면 재귀적으로 접근하지 않고 바로 값을 반환하도록 했다.
아래는 위의 두가지 구현에 대해 걸리는 시간을 측정한 결과이다. 보시는 바와 같이 차이가 심하다.
n=50 r=8
bino_coef : 2815ms
bino_coef_dp : 0msDynamic Programming을 이용한 조금 다른 구현
한 블로그에서 이항 계수을 확장성이 매우 뛰어난 방법으로 구현한 것을 보았다. 위에서는 이항 계수의 성질에서 나오는 공식을 이용하여 이항 계수를 구현하였다. 그러나 이항 계수의 개념인 n개의 아이템 중 r개의 아이템을 뽑는 조합의 수를 직관적으로 이용한 구현을 설명하고자 한다.
n개의 아이템 중 r개의 아이템을 뽑는 경우의 수는 아이템을 선택할 기회가 n번 있을 때 r개를 뽑은 경우의 수와 일치한다. 아이템을 선택할 수 있는 기회는 총 n번이며, 각 기회에서 선택할 수 있는 전략은 뽑거나 뽑지 않는 것이다. 즉, 우리는 첫번째 아이템부터 시작하여 한번씩 선택을 하며, n번째 아이템까지 선택하였을 때 k개가 뽑힌 경우의 수를 구하면 되는 것이다.
아래는 이를 구현한 코드이다.
typedef long long ll;
// 이항계수를 좀더 범용적인 경우에 사용할 수 있도록 구현한 방식
// 직접 아이템을 뽑아가며 경우의 수를 구한다.
ll bino_coef_dp2(int n, int r){
// r이 n보다 큰 경우의 수는 0이다.
if (r > n)
return 0;
// Memoization을 위한 이차원 배열 선언
ll **dp = new ll*[n + 1];
for(int i = 0; i <= n; i++){
dp[i] = new ll[n + 1];
for(int j = 0; j <= n; j++)
dp[i][j] = -1;
}
// 실제로 뽑아가며 경우의 수를 구함.
ll result = choose(n, r, dp, 0, 0);
// 할당된 메모리 해제
for(int i = 0; i <= n; i++)
delete[] dp[i];
delete[] dp;
return result;
}
// 이항 계수를 원소를 실제로 뽑아가며 경우의 수를 구함.
// n개의 원소 중 r개를 뽑아야하는데, 현재까지 원소를 times번 선택하였으며, got개의 원소를 뽑은 상태이다.
ll choose(int n, int r, ll **dp, int times, int got){
// n번 선택했으면 재귀함수를 탈출한다.
if (times == n)
return got == r; // 선택한 원소의 개수가 r개면 true(1), r개가 아니면 false(0)을 반환한다.
// 해당 부분 문제가 이미 계산되어 있으면, 바로 반환한다.
if (dp[times][got] != -1)
return dp[times][got];
// times번째 선택에서 뽑는 경우 + times번째 선택에서 뽑지 않는 경우
return dp[times][got] = choose(n, r, dp, times + 1, got) + choose(n, r, dp, times + 1, got + 1);
}bino_coef_dp2()는 Memoization을 위한 배열의 초기화의 역할이고, 실제로 경우의 수를 구하는 과정은 choose()에서 이루어진다. choose()함수에서 times인자는 현재까지 선택한 원소의 개수이며, got 인자는 현재까지 몇개의 원소를 뽑았는지를 나타낸다.
재귀 함수의 탈출 조건은 times == n일때 즉 n번 선택하였을 때이며, 이때 got == r을 통해 이제껏 뽑은 원소의 개수가 r개이면 1을 반환하고, 아니면 0을 반환한다.
Memoization을 통해 이미 계산한 부분문제에 대해서는 바로 값을 반환하도록 하였다.
해당 구현을 통한 문제의 확장
이항 계수를 위처럼 구현한 이유를 확장성때문이라고 하였다. 이게 어떤 의미인지는 이번 장에서 설명할 것이다.
기존의 구현에서는 n개의 아이템 중 r개를 선택하는 경우의 수를 구할 수 있다. 그러나 만약 n개의 아이템 중 r개 이상을 선택하는 경우의 수를 구하고 싶다면 어떻게 해야할까? 기존의 구현대로라면 bino_coef_dp(n,r) + bino_coef_dp(n,r + 1) + ... + bino_coef_dp(n,n)처럼 함수를 여러번 호출하여야 한다. 그러나 bino_coef_dp2()의 경우는 함수를 조금만 수정해주면 바로 해결이 가능하다.
// n번 선택했으면 재귀함수를 탈출한다.
if (times == n)
return got == r; // 선택한 원소의 개수가 r개면 true(1), r개가 아니면 false(0)을 반환한다.choose()에서 n번만큼 선택을 하여 재귀함수를 탈출할 때, got == r라는 식을 반환한다. 이는 뽑은 원소의 개수가 r개일 때 true 즉 1을 반환한다는 뜻이며, 경우의 수가 1개 있다는 의미이다. 그렇다면 이 식을 got >= r로 바꾸면 어떻게 될까? 뽑은 원소의 개수가 r개 이상일 때 true를 반환하며, 즉 경우의 수에 포함이 된다는 의미이다.
// n번 선택했으면 재귀함수를 탈출한다.
if (times == n)
return got >= r; // 뽑은 원소의 개수가 r개 이상이면 true를 반환한다.위와 같이 코드를 수정하면 n개의 아이템 중 r개 이상을 선택하는 경우의 수를 구할 수 있다.
n개의 아이템 중 r개를 선택하는 경우의 수는 n번을 시도했을 때 r번을 성공하는 경우의 수로도 생각할 수 있으며, 이를 통해 n번을 시도했을 때 r번을 성공하는 확률 또한 구할 수 있을 것이다.
예를 들어 동전을 n번 던질 때 앞면이 r개가 나오는 확률을 계산하는 문제가 있다. 이 때에는 choose()에서 아래 코드를 수정하면 된다.
// times번째 선택에서 뽑는 경우 + times번째 선택에서 뽑지 않는 경우
return dp[times][got] = choose(n, r, dp, times + 1, got) + choose(n, r, dp, times + 1, got + 1);현재는 dp[times][got]에 경우의 수를 저장하고 있다. 하지만 이 코드를 다음과 같이 바꾸어보자. (dp 배열 역시 소수 자료형으로 바꾸어야 한다.)
return dp[times][got] = 0.5 * choose(n, r, dp, times + 1, got)
+ 0.5 * choose(n, r, dp, times + 1, got + 1);동전을 던지는 경우, 앞이 나올 확률과 뒤가 나올 확률은 모두 0.5이다. 그래서 각각의 경우의 수에 해당 경우가 일어날 확률인 0.5를 곱해줌으로써 확률을 구할 수 있다.
위에서 r개 이상의 원소를 뽑는 경우의 수와 확률을 구하는 방법에 대해 알아봤다. 이 두개를 조합해 동전을 n번 던져 앞면이 r개 이상 나오는 확률을 구하는 함수를 구현해보면 다음과 같다. bino_coef_dp2() 함수는 그대로 사용하면 된다.
ll choose(int n, int r, double **dp, int times, int got){
// n번 선택했으면 재귀함수를 탈출한다.
if (times == n)
return got >= r; // r개 이상 뽑힌 경우 1 반환
// 해당 부분 문제가 이미 계산되어 있으면, 바로 반환한다.
if (dp[times][got] != -1)
return dp[times][got];
// 확률을 구함
return dp[times][got] = 0.5 * choose(n, r, dp, times + 1, got)
+ 0.5 * choose(n, r, dp, times + 1, got + 1);
}페르마의 소정리
이항계수에서 n과 r의 값이 커지면 경우의 수도 매우 많아진다. 그렇기 때문에 경우의 수에 모듈러 연산을 취한 값을 원하는 경우가 있다. 이때 페르마의 소정리를 이용하면 이항계수를 굉장히 빠르게 구할 수 있다.
우선 페르마의 소정리란, p가 소수이고 a가 정수일 때, 다음을 만족한다는 것이다.
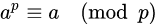해당 공식의 의미는 ap를 p로 나눈 나머지가 a를 p로 나눈 나머지와 같다는 것이다. 즉 다음과 같다.
ap % p == a % p
여기에서 양변을 a로 나누어주면 다음과 같은 식을 얻을 수 있다.
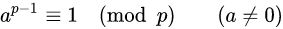또한, 여기서 한번 더 양변을 a로 나누어 주면 ap-2 = a-1 (mod p)임을 알 수 있다.
이제 페르마의 소정리를 이항계수에 적용시켜보자.
nCr = n! / (r! (n - r)!) (mod p) 일때, A = n!, B = (r! (n - r)!) 이라 대입하자.
그럼 n! / (r! (n - r)!) % p = (A * B-1) % p = ((A % p) * (B-1 % p))가 된다.
여기에서 B-1은 Bp-2와 같은 값이 된다.
즉, nCr = (A * Bp-2) % p라는 공식이 나오게 되며, 분수가 아닌 정수의 곱으로 이항계수를 표현할 수 있게 된다. 정수의 곱으로 표현하고자 하는 이유는, 분수에는 모듈러 연산을 바로 적용하기가 힘들기 때문이다.
위처럼 정수의 곱으로 이항계수를 표현하였으면, p-2승만큼 거듭제곱을 해주어야 한다. 거듭제곱을 구하는 방법은 여러개 있겠지만, 값을 빠르게 구하기위해 2진법을 이용하여 구해보자.
모든 숫자는 2의 지수승의 합으로 나타낼 수 있으며 이를 이용해 지수를 다음과 같이 분리할 수 있다.
312 = 38 * 34
이러한 성질을 이용해 3n을 O(logn)의 시간복잡도로 구할 수 있다.
구현은 다음과 같다.
int result = 1; // 결과 값
int base = 3; // base
int exponent = 12; // 지수
while(exponent){
if (exponent % 2){
result *= base;
result %= MOD;
}
base *= base;
base %= MOD;
exponent /= 2;
}페르마의 소정리를 이용하여 이항계수를 구현할 때는 모듈러 연산이 적용되니 이에 맞게 코드를 수정하면 다음과 같다.
int result = 1; // 결과 값
int base = 3; // base
int exponent = 12; // 지수
while(exponent){
if (exponent % 2){
result *= base;
result %= MOD;
}
base *= base;
base %= MOD;
exponent /= 2;
}마지막으로 최종적인 구현코드는 다음과 같다.
typedef long long ll;
// 페르마의 소정리를 이용한 이항 계수 구하기.
// 모듈러 연산을 취하는 것이 전제되어있다.
ll bino_coef_ferma(int n, int r){
ll MOD = 1000000007LL;
ll A = 1, B = 1; // A = n!, B = k!(n-k)!
// n! 구하기
for(ll i = 1; i <= n; i++){
A *= i;
A %= MOD;
}
// k! 구하기
for(ll i = 1; i <= r; i++){
B *= i;
B %= MOD;
}
// k!(n-k)! 구하기
for(ll i = 1; i <= n - r; i++){
B *= i;
B %= MOD;
}
// B^(MOD-2)를 구함. 2진수 표현을 통해 O(logN)의 시간복잡도로 구한다.
ll B2 = 1;
int exponent = MOD - 2;
while(exponent){
if (exponent % 2){
B2 *= B;
B2 %= MOD;
}
B *= B;
B %= MOD;
exponent /= 2;
}
// 최종 결과를 구한다.
ll result = A * B2;
result %= MOD;
return result;
}참고 링크
https://shoark7.github.io/programming/algorithm/3-ways-to-get-binomial-coefficients
https://cru6548.tistory.com/23
