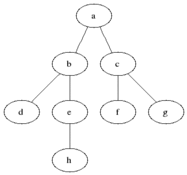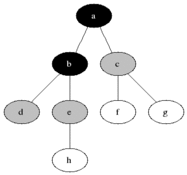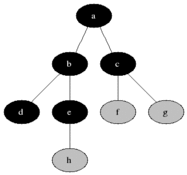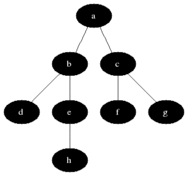
너비 우선 검색 (Breadth First Search, BFS)

쉽게 말해 가까운 노드부터 탐색하는 알고리즘. BFS는 선입선출 방식의 큐를 이용하면 효과적.
인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어 가까운 노드부터 탐색한다.
출처 - 이것이 코딩테스트다 with python p.338

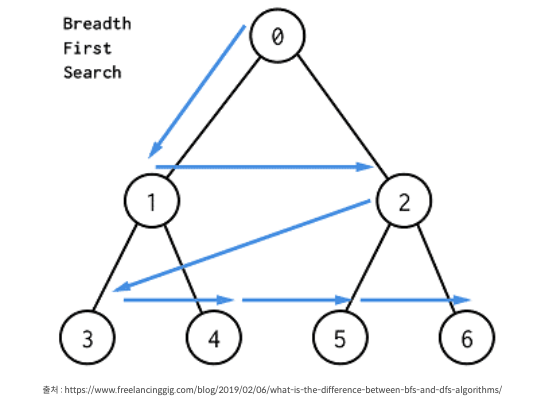
너비우선탐색법은
1. 출발점(source)로부터 도달할 수 있는 모든 정점을 '발견'하기 위해 간선을 체계적으로 탐색하고,
2. 각 정점까지의 최단거리(가장 적은 간선으로 도달한 것)를 큐를 이용하여 계산하며,
3. 너비우선트리(s를 루트로 하고 s에서 닿을 수 있는 모든 정점을 가지는 트리)를 만든다.

이를 구현할 때 각 정점에 흰색, 회색, 검은색을 표시한다. 몇가지 룰이 있다.
1. 처음 발견 되면 흰색을 다른색으로 칠한다.
2. 검은색 정점에 인접해 있는 모든 정점은 이미 발견된 것이다.
3. 회색 정점은 옆에 흰색 정점을 가질 수 있다.

여기서 회색은 발견 된 것과 안된 것의 사이에 있는데 frontier라고 불린다.

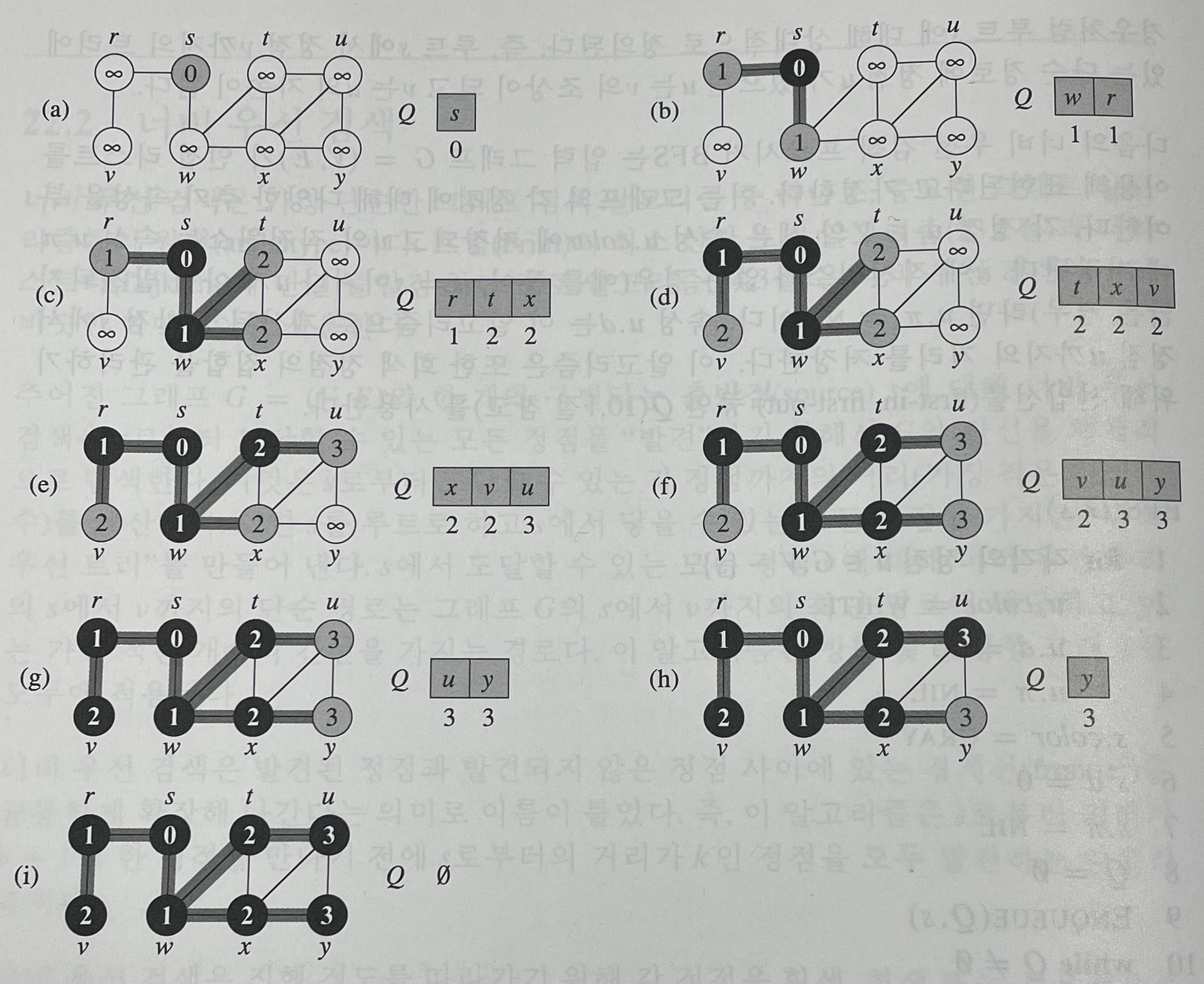
그림이 조금 불친절하니 gif를 넣었다.

G = (V, E)
V: 정점(vertax) 개수
E: 간선(edge) 개수

그래프 G = (V,E)를 표현하는 방법에는 인접리스트의 집합을 사용하는 것과 인접행렬을 사용하는 방법이 있는데 작은 밀도 그래프에는 인접리스트로 가정하는것이 더 효율적이다.

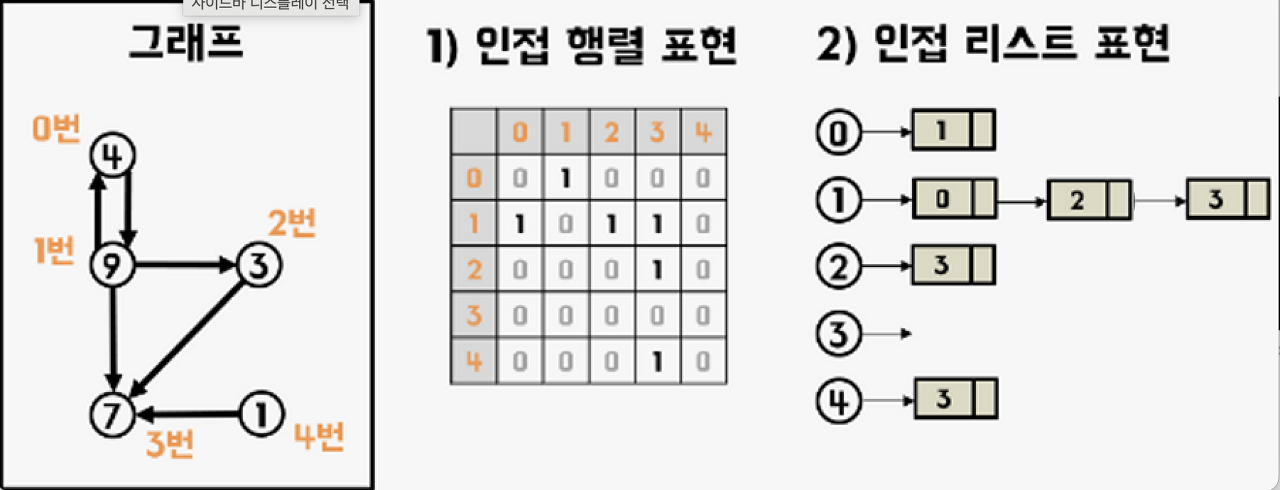
몇가지 특징

• 이미 발견된 정점 : u
• u의 인접리스트에 연결된 흰 정점 : v
• u는 v의 직전원소or부모 이다.
• 큐에 넣거나 제거하는 연산 시간 복잡도 : O(1)
• 큐에 연산하는데 총 걸리는 시간 복잡도 : O(V)
• BFS는 각 인접 리스트를 최대 한 번만 스캔한다.(정점이 삭제될 때만 인접리스트가 스캔됨)
• 인접 리스트를 스캔하는데 걸리는 시간 : O(E) <- E:간선개수
• 초기화 : O(V) <- 정점개수
• -> 따라서 BFS 수행시간 : O(V+E) 즉, O(정점개수+간선개수)

의사코드

# 1 procedure BFS(G, start_v) is 
# 2      let Q be a queue                      //Queue 생성
# 3      label start_v as discovered           //시작 루트 정점을 방문 표시하기
# 4      Q.enqueue(start_v)                    //큐에 시작 루트 정점 넣기
# 5      while Q is not empty do               //큐가 빈 공간이 아닐 때까지 아래 반복
# 6          v := Q.dequeue()                  //현재 방문할 정점 v를 Queue에서 꺼낸다.
# 7          for all edges from v to w in G.adjacentEdges(v) do // v와 인접한 모든 정점 w에 대하여
# 8             if w is not labeled as discovered then // w가 방문표시 되지 않았으면
# 9                 label w as discovered      // w를 방문표시하고
# 10                Q.enqueue(w)               //w를 Queue에 넣는다.

구현코드

def bfs(start_v):
    visited = [start_v]
    Q = deque([start_v])
    while Q:
        v = Q.popleft()
        for w in graph[v]:
            if w not in visited:
                visited.append(w)
                Q.append(w)

    return visited

장점

• 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.

단점

• 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
• 해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
• 무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.

관련 알고리즘 문제
https://www.acmicpc.net/problem/1260

그래프 관련 용어

• Vertex(=Node, 정점): Tree에서의 Node와 같은 개념
• Edge(=Link, 간선): 정점과 정점을 있는 선
• Weight: 간선의 크기가 있는 경우 그 가중치값
• Degree: 정점에 연결되어 있는 간선의 수
• out-degree: 방향이 있는 그래프에서 정점에서부터 출발하는 간선의 수
• in-degree: 방향이 있는 그래프에서 정점으로 들어오는 간선의 수
• Path: 정점 V_i에서 V_j까지 간선으로 연결된 정점을 순서대로 나열한 리스트 e.g. A → E = {A, B, D, E}
• Path Length: 경로를 구성하는 간선의 수
• Cycle: 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로 e.g. A→ A = {A, B, D, A}
  출처 : 링크텍스트