1020-TIL(DFS)

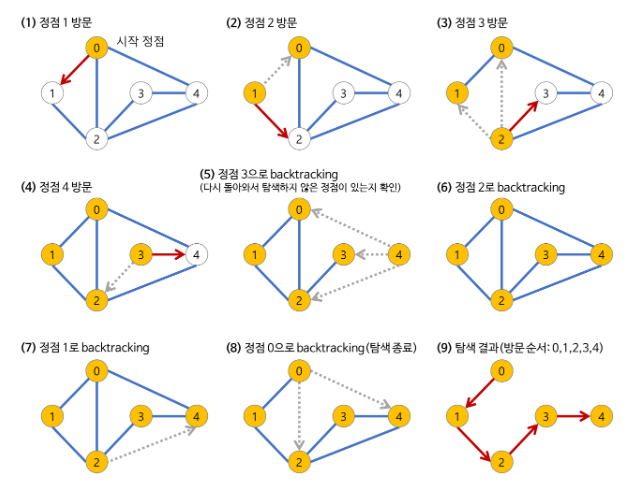
어제 BFS를 공부할 때는 알고리즘 벽돌 책을 먼저 정독하고 부족한 부분을 인터넷 자료로 보충했는데, 시간이 오래 걸린 기분이라 오늘은 반대로 인터넷으로 다른 사람이 이미 정리한 것부터 먼저 빠르게 정리하고 부족한 부분을 벽돌 책 읽을 예정이다.

Depth-First Search.
깊이 우선 탐색 알고리즘은 최대한 멀리 있는 노드를 우선으로 탐색하는 방식으로 동작하며 스택 자료구조를 이용한다.
출처 - 이것이 코딩테스트다 with python p.338

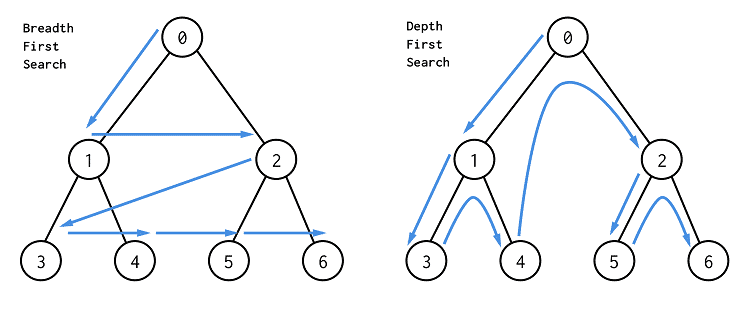
오른쪽이 DFS의 탐색 순서를 그림으로 표한 것이다.

아래 기본 개념부터 시간과 저장공간 분석까지는 위키백과를 참고한 내용이다.링크텍스트

기본 개념

DFS는 맹목적 탐색 방버의 하나로 탐색트리의 최근에 첨가된 노드를 선택하고, 이 최근 노드에 적용 가능한 동작자 중 하나르 ㄹ적용하여 트리에 다음 레벨의 한 개의 자식 노드를 첨가한다. 첨가된 자식 노드가 목표노드가 될 때까지 앞의 자식 노드의 첨가 과정을 반복해 가는 방식이다.

깊이 제한과 백트래킹

탐색 과정이 시작 노드에서 한없이 깊이 진행되는 것을 막기 위해 깊이 제한(depth bound)을 사용한다. 깊이 제한에 도달할 때까지 목표노드가 발견되지 않으면 최근에 첨가된 노드의 부모노드로 되돌아와서, 부모노드에 이전과는 다른 동작자를 적용하여 새로운 자식노드를 생성한다. -> N퀸에서 마치 내려가다가 체스판 끝에 도달하면 다시 올라가서 다른 길 찾는 것과 같은 말임...
여기서 부모노드로 되돌아오는 과정을 백트래킹(backtracking)이라 한다.

알고리즘

만일 트리가 아닌 그래프를 탐색하게 된다면 약간의 변화가 필요하다. 트리는 순환 되는 구조가 아니기 때문에 깊이를 걱정할 필요가 없지만 그래프는 깊이를 결정할 필요가 있다.
일반적으로 그래프에서는 루트 노드의 깊이를 0으로 하며, 임의의 노드의 깊이는 이의 부모 중 가장 깊이가 작은 것의 깊이에 1을 더한 값으로 정의한다. 따라서 그래프에서의 깊이우선탐색은 OPEN에 있는 노드 중 가장 깊은 것을 택하여 확장시키게 된다. 후계 노드가 생성되어 이 중에 이미 OPEN이나 CLOSED에 있는 것이 있다면, 깊이를 재조정하여야 한다.

여기서 알 수 있는 것은 일반적인 그래프를 탐색하는 경우라도, 탐색 과정에 의하여 얻어지는 노드들과 포인터들은 역시 탐색 트리를 형성한다는 것이다. 즉, 포인터들은 오직 하나의 부모를 가리키게 된다.

장점과 단점

[장점]

• 단지 현 경로상의 노드들만을 기억하면 되므로 저장공간의 수요가 비교적 적다. (bold처리 부분은 아직 이해 안감)
• 목표노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
  단점

[단점]

• 해가 없는 경로에 깊이 빠질 가능성이 있다. 따라서 실제의 경우 미리 지정한 임의의 깊이까지만 탐색하고 목표노드를 발견하지 못하면 다음의 경로를 따라 탐색하는 방법이 유용할 수 있다.
• 얻어진 해가 최단 경로가 된다는 보장이 없다. 이는 목표에 이르는 경로가 다수인 문제에 대해 깊이우선 탐색은 해에 다다르면 탐색을 끝내버리므로, 이때 얻어진 해는 최적이 아닐 수 있다는 의미이다.

시간과 저장공간 분석

깊이 우선 탐색에서 필요로 하는 시간과 저장공간을 분석해 보면, 일반적으로는 시간에 대해 말하기가 좀 어려운데, 이는 트리가 무한할 경우, 깊이우선 탐색은 목적을 만족시키는 노드를 찾지 못할 수도 있을 뿐 아니라 알고리즘이 끝나지 않을 수도 있기 때문이다. 트리의 깊이가 목적 노드 깊이와 같을 때에는 최악의 경우 모든 노드를 다 검사하게 된다.
저장공간의 사용량을 계산해 보면 좀 더 희망적인 결과를 얻을 수 있다.
연구 결과에 따르면 깊이우선 탐색은 저장공간의 사용에 있어서 점근 최적인 것으로 알려져 있다.

BFS vs DFS

[직전 원소 부분 그래프가 make one tree or multiple trees]

• BFS의 직전원소 부분그래프(predecessor subgraph)는 하나의 트리를 형성
• DFS 직전원소 부분 그래프에서는 여러 개의 트리로 구성될 수 있음.
  -> 왜냐하면 검색이 여러 출발 점들로부터 반복할 수 있기 때문.

[직전원소 부분그래프의 내용 다름]

• DFS는 그냥 트리 아니라 깊이 우선 트리로 구성된 깊이 우선 forest를 형성한다.

[정점 상태를 나타내기 위한 색칠하기]

• DFS 에서는 처음엔 흰색(여긴 같음), 발견됐을 때는 회색, 종료 됐을 때(즉,인접리스트가 완전히 검사되었을 때)는 검은색 됨
  -> 이 기법이 보장하는 것: 각 정점이 하나의 깊이 우선 트리에만 포함되어 트리가 서로 공통인 부분이 하나도 없음을 보장.

• BFS는 어땠냐면 처음엔 흰색은 같고, 발견하면 회색, 발견한 회색은 검은색칠하고 인접 정점들을 회색으로 칠함.

[DFS 는 시간을 기록 함]

• BFS는 최단 거리를 기록하기 위해 정점 간의 거리를 큐에 기록하는데
• DFS는 시간을 기록한다.
  각 정점은 두 개의 시간 기록을 가진다. 첫번째 시간기록은 v가 처음으로 발견됐을 때(when its painted to 회색), 두번째 시간기록은 v의 인접리스트 조사를 마쳤을 때(when its painted to 검은색)

아래는 재귀로 구현한 것을 의사코드로 표현한 것이다.

DFS 과정

위 그림 출처

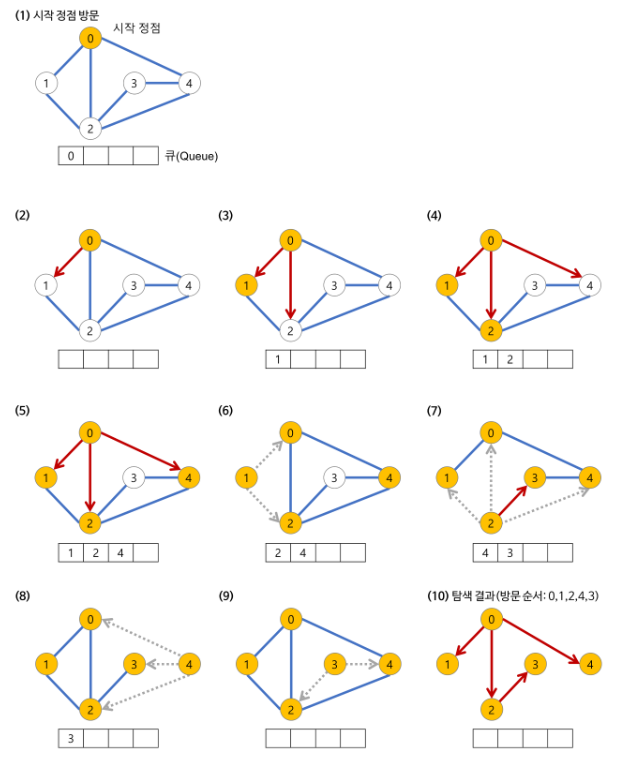
참고 - BFS 과정

의사코드 using visited

DFS(G, v)
    visit v;
    mark v as visited;
    for all directed edges from v to w that are in G.adjacentEdges(v) do
        if vertex w is not marked as visited then
            recursively call DFS(G, w)

아래는 위의 의사코드를 파이썬으로 표현한 것이다.

구현코드 using visited

def recursive_dfs(v, visited=[]):
    visited.append(v)
    for w in graph[v]:
        if not w in visited:
            visited = recursive_dfs(w, visited)
    return visited

재귀를 쓰는게 부담스럽다면 스택을 이용하면 반복문을 통해서도 구현이 가능하다.

의사코드 using stack

DFS_iterative(G,v)
    let S be a stack
    S.push(v)
    while S is not empty do
        v = S.pop()
        if v is not marked as visited then   // 첫 방문시
            mark v as visited
            for all edges from v to w in G.adjacentEdges(v) do
                S.push(w)

아래는 위의 의사코드를 파이썬으로 표현한 것이다.

구현코드 using stack

def iterative_dfs(start_v):
    visited = []
    stack = [start_v]
    while stack:
        v = stack.pop()
        if v not in visited:
            visited.append(v)
            for w in graph[v]:
                stack.append(w)

return visited

책에서 찾은 특성

출처-Introduction to algorithms p.621
[두 개의 시간 표현 방법]

• 발견 시간과 종료 시간이 괄호 구조이다.
• 정점 u를 발견하면 왼쪽 괄호 like "(u"
  종료는 오른쪽 괄호 like "u)"

아래 사진의 b 참조

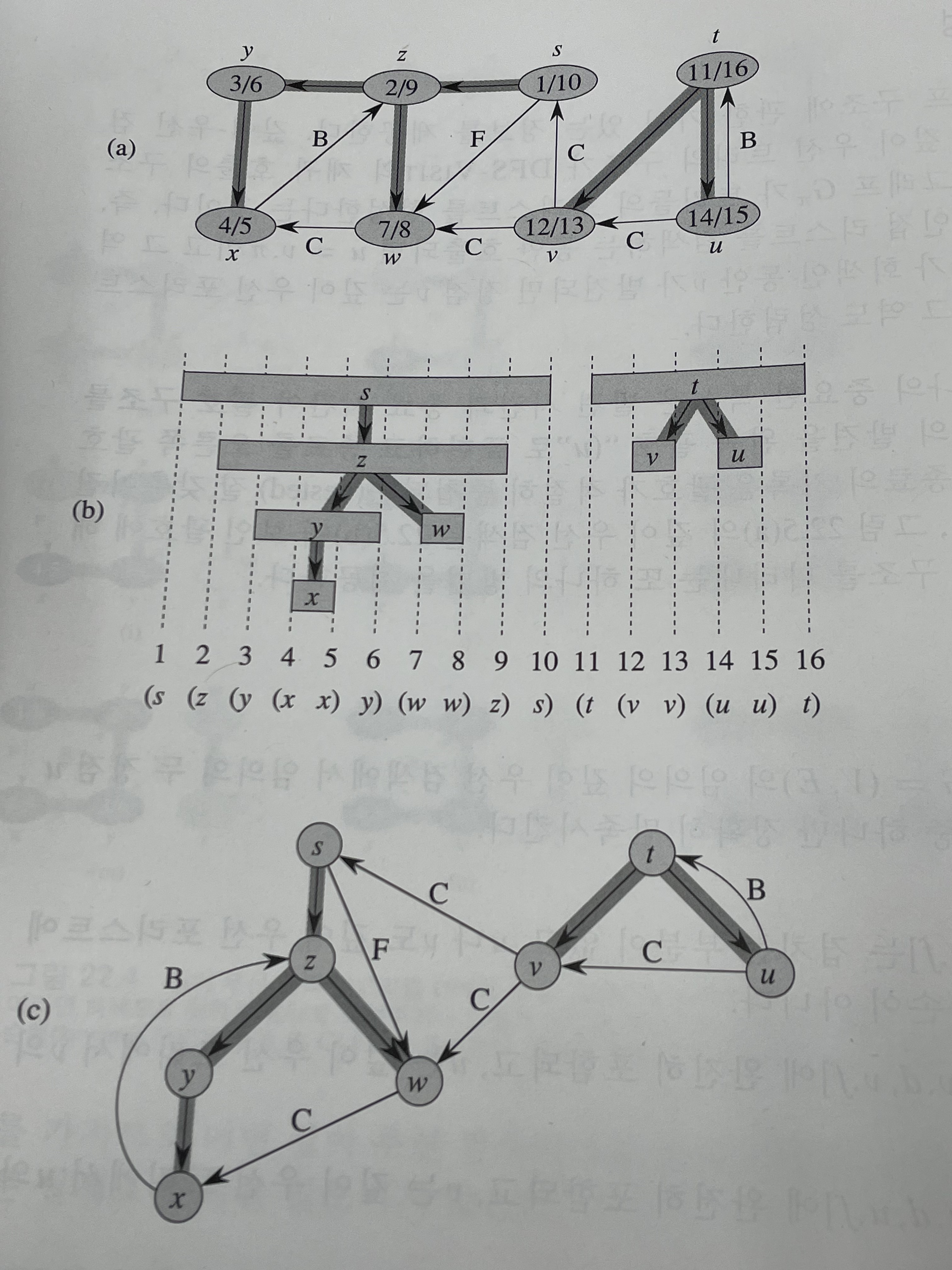
[탐색 정도를 간선으로 분류함]

• 트리간선(Tree edge) -> white
  간선 (u,v)를 검색하여 처음 발견 되었다면 트리간선

• 역행간선(Back edge) -> grey
  정점 u를 한 조상 v에 연결하는 간선.

• 순행간선(Forward edge) -> black
  정점 u를 한 자손 v에 연결하는 트리 간선이 아닌 간선. 그니까 다른 자손 정점으로 연결이 안되어 있는 간선인듯.

• 교차간선(Cross edge) -> black
  나머지 모든 간선.
  하나의 정점이 또 다른 정점의 조상이 아니어야 함.
  교차 간선은 같은 우선트리에 있는 두 정점 사이에 존재할 수도 있고, 서로 다른 깊이 우선트리에 있는 두 정점 사이에 있을 수도 있음.

효율성

공간 복잡도

[인접행렬] : O(V^2)
그래프,visited, stack 다 같음

[인접리스트] : O(V+E)
정점 개수 + 간선 개수
스택과 visited 모두 O(n) <- 정점 개수. 인접 행렬이던 인접 리스트이던 해당.

시간 복잡도

[인접리스트] : O(V+E) 정점개수+간선개수

• 한 번 방문한 지점은 다시 방문하지 않는다.
• 하나의 정점에서 다음으로 방문할 다른 정점들을 순회하는 횟수가 그 정점의 간선의 개수와 같기 때문이다.

[인접행렬] : O(V^2) 정점의 개수의 2제곱

• DFS()를 호출하는 횟수는 |V|번이다.
• 다음에 방문할 정점을 찾을 때 모든 정점을 순회하며 두 정점이 연결되어 있는지 확인해야 하기 때문이다.