1. 빅-오(Big-O) 표기법이란?
점근 표기법(asymptotic notation)은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다. 알고리즘의 복잡도를 단순화할 때나 무한급수의 뒷부분을 간소화할 때 쓰인다. 이 중 압도적으로 많이 쓰이는 것이 대문자 O 표기법, Big-O 표기법이다. 이 Big-O 표기법은 계수와 낮은 차수의 항을 제외시키는 방법이다.
점근 표기법의 세가지 방법
- 최상 : 오메가 표기법 (Big-Ω Notation)
- 평균 : 세타 표기법 (Big-θ Notation)
- 최악 : 빅오 표기법 (Big-O Notation)
Big-O 표기법은 점근 표기법 중 가장 많이 사용되는 표기법으로 알고리즘의 효율성을 분석할때 사용한다.
Big-O 표기법을 사용하는 이유는, 평균을 나타내는 세타 표기법이 가장 이상적이고 정확하지만, 도출하기가 상대적으로 어려워서 알고리즘의 최악의 경우를 판단하면 평균과 가까운 성능으로 예측이 가능하여 Big-O 표기법을 사용한다.
이러한 Big-O 표기법은 아래와 같이 계수항과 낮은 차수 항을 제외 시키는 방법이다.
- 계수 항 무시
O(3N) > O(N)
- 낮은 차수 항 무시
O(N²+2N) > O(N²)
- 빅-오 표기법의 성능(수행시간, 연산횟수)
O(1) < O(log n) < O(n) < O(n * log n) < O(n²) < O(n³) < O(2^n) < O(n!)
- O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
- O(log n) – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
- O(n) – 직선적 시간 : 문제를 해결하기 위한 입력 N 만큼의 단계가 필요.
- O(n log n) : 문제를 해결하기 위한 단계의 수가 N번에 그 하나의 N번당 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
- O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
- O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
아래는 Big-O의 복잡도를 나타내는 표이다.
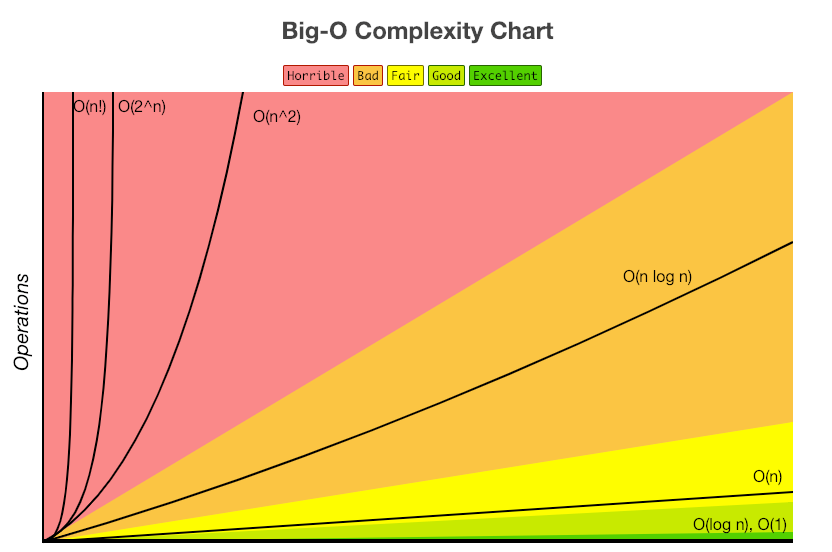
이러한 Big-O 표기법에는 시간복잡도와 공간복잡도 가 존재한다.
2. 시간복잡도와 공간 복잡도(Time Complexity & Space Complexity) 예제
시간복잡도는 알고리즘의 속도에 해당하는 연산시간의 분석결과이다.
시간 복잡도는 연산 수행에 어떤 고정된 시간이 걸릴 때, 알고리즘에 의해서 수행되는 기본 연산의 개수를 세어 예측할 수 있다.
아래 자바 예제를 통해서 알아보자.
만약, 입력 N에 대해서 N²을 구하는 함수를 작성한다고 하면, 아래와 같이 여러가지 방법이 있고 각각의 시간복잡도는 다르다.
// 곱셈 연산을 1개 사용하므로 O(1)
int multiple(int N){
return N*N;
}
// 덧셈 연산 1개와 대입 연산 1개가 N번씩 실행되므로 O(2N) > O(N)
int multiple2(int N) {
sum = 0;
for(int i = 1 ; i < = N; i++{
sum += N;
}
return sum;
}
// 덧셈 연산 1개와 곱셈 연산 1개가 N번씩 성립되므로 2N > 그 2N연산이 N번 실행되므로
// O(2N²) > O(N²)
int multiple3(int N){
sum = 0;
for(int i = 1; i <= N; i++){
for(int j = 1; j <= N; j++){
sum += 1;
}
}
return sum;
}
공간복잡도는 알고리즘을 사용할 때 메모리 사용량을 나타낸다.
만약 크기가 N인 배열을 만들면 공간 복잡도가 O(N)이 되고, N²인 배열을 만들면 O(N²)이 된다.
재귀 함수 호출의 경우 스택 공간을 고려 해야 한다.
1부터 N까지의 합을 구하는 예제를 재귀를 통해 구현 하면 아래와 같이 공간 복잡도가 O(N)이 된다.
// N = 3일때 스택에 쌓이는 메모리는 sum(1) + sum(2) + sum(3), 공간 복잡도가 O(N)이다.
int sum(int N){
sum = 0;
if(N<1)
return 0;
return N + sum(N-1);
}
하지만 N번의 호출이더라도 아래와 같이 호출하면 공간 복잡도가 O(1)이 된다.
// mainSum에서 N번 sum을 호출하지만 for문 안에서
// sum(i, i+1)의 값을 주어지며 스택안에서 계산되어
// result에 더해지므로 O(1)의 공간을 사용한다.
int mainSum(int N){
int result = 0;
for(int i=0; i<N; i++)
result += sum(i, i+1);
return result;
}
int sum(int a, int b){
return a + b;
}
3. 정렬 알고리즘 시간복잡도 비교

- 단순(구현 간단)하지만 비효율적인 방법
- 삽입 정렬, 선택 정렬, 버블 정렬
- 복잡하지만 효율적인 방법
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
- 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬
🙆♂️ 참고사이트 🙇♂️
빅오 표기법 (Big-O Notation), 시간 복잡도, 공간 복잡도[Juhun님]
