탐욕 알고리즘(Greedy Algorithm)

GilLog·2020년 10월 8일

알고리즘

목록 보기

2/8

💥❗ 주의사항 ❗💥

본 게시글은 작성자 본인의 학습을 위함이라 부족한 점이 많습니다.
선생님들의 따뜻한 조언과 피드백 부탁드립니다! 감사합니다! 🙇‍♂️

1. 탐욕 알고리즘이란?

탐욕 알고리즘에 대해서는 지난번 동적 계획법(Dynamic Programming)에 대해서 정리하면서 대략적으로 알게 되었다.
이때 탐욕 알고리즘에 대해 알게 된 사실은
동적 계획법(Dynamic Programming)은 모든 경우를 검토하여 최적의 답을 찾아 내는 방법.
탐욕 알고리즘(Greedy Algorithm)은 매 순간 최적인 경우를 찾아가면서 최적의 답을 찾아 내는 알고리즘 이라는 것이었다.

이번엔 조금 더 자세하게 탐욕 알고리즘에 대해서 알아보려고 한다.

탐욕 알고리즘(Greedy Algorithm)은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다. 하지만 탐욕알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다.
-WikiPedia

한마디로 정리하면 현재 선택에서 최적인 것들을 마지막 선택까지 해나가서 답을 구하는 알고리즘이다.

이러한 탐욕 알고리즘은 근시안적인 알고리즘이라는 표현도 존재한다.
왜 인지는 아래의 경우를 통해 살펴보자.

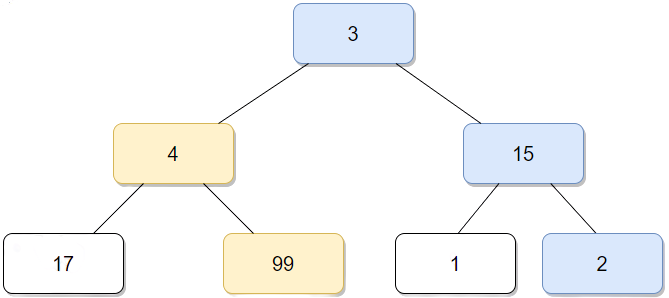
아래로 내려가면서 정한 숫자들을 합쳐서 가장 큰 합을 만드는 문제라고 가정해보자.

탐욕 알고리즘으로 이 문제를 접근하면 파란색처럼 첫번째 선택에서 15를 선택하고 그 다음 선택에서 2를 선택해서 최종 답은 20이 된다.

하지만 실질적으로 이 문제에서 최적의 답은 노란색으로 첫번째 선택에서 4를 선택하고 그 다음 선택에서 99를 선택해서 최종 답이 106이 된다.

탐욕 알고리즘으로 접근하니 첫 번째 선택에서 4가 아닌 최적의 선택인 15를 선택했지만 전역적(최종적)답이 최적의 답이 아니게 되었다.

그럼 어떤 문제들에 탐욕 알고리즘을 적용 할 수 있을까?

2. 탐욕 알고리즘의 조건

탐욕 알고리즘은 DFS/BFS, DP들 보다 빠른 속도때문에 적용 할 수 있다면 가장 빠르게 결과를 얻을 수 있다.
그렇다면 빠르게 탐욕 알고리즘이 적용 가능한지 파악하는 것이 중요한데, 탐욕 알고리즘을 적용하려면 탐욕스런 선택 조건(Greedy Choice Property)과 최적 부분 구조 조건(Optimal Substructure)이라는 두 가지 조건이 만족 되어야 한다.

그렇다면 이 조건들은 무엇일까?

2.1 최적 부분 구조(Optimal Substructure)

최적 부분 구조(Optimal Substructure)은 앞서 동적 계획법(Dynamic Programming)에서 살펴 보았듯이 작은 부분 문제에서 구한 최적의 답으로 합쳐진 큰 문제의 최적의 답을 구할 수 있어야 한다는 것이다.

탐욕 알고리즘의 대표적인 문제인 거스름돈 문제를 통해서 살펴보자.

만약 손님이 10,000원을 가지고 있다고 가정하자.
나는 가게의 점원으로 계산할때 잔돈은 항상 적은 개수의 동전을 주어야 한다고 가정하자.
동전은 10원, 50원, 100원, 500원이 있을때,
물건 값이 입력 될때 잔돈의 최소 동전 개수를 구하라.
(동전의 개수는 충분한 상황)

이러한 문제에서 손님이 5250원짜리 물건을 구매했다고 하면, 잔돈은 4750원이 된다.
1000원 단위는 제외하고 750원을 동전으로 주어야 하는 상황에서 아래와 같은 과정으로 동전의 개수를 구할 수 있다.

750원
- 최적의 선택 500원 차감 동전 개수 : 1
250원
- 최적의 선택 100원 * 2개 차감 동전 개수 : 2
50원
- 최적의 선택 50원 차감 동전 개수 : 1
최소 동전은 4개

최종적으로 750원에서 최소한의 동전 개수를 구하는(큰 문제)는 현재 남은 금액(750원, 250원, 50원)보다 작으면서 가장 금액이 큰 동전(최적)의 최대 개수 구하기 문제(부분 문제)의 개수 합으로 구할 수 있으므로 최적 부분 구조를 만족한다.

최소 동전의 개수를 구하는 문제는 사실상 거스름돈 금액에서 조합 가능한 가장 큰 금액의 동전의 조합을 찾아서 그 개수를 구하는 문제이다.

이를 부분 문제로 쪼개면 현재 금액보다 작으면서 가장 큰 금액의 동전을 찾고 이를 현재 금액에서 빼주고 개수를 세주면 된다.

이를 코드로 바꾸면 아래와 같다.


int change = 10000 - N;
int result = 0;

// 1000원 이상 지폐는 제외 해주기 위해
change %= 1000;

int [] coins = {500,100,50,10};

for (int coin : coins){
	// 코인이 잔돈보다 크면 통과
	if(coin > change)
    	    continue;
    // 나눠주어서 몇개 까지 바꿔줄수 있는지 세주기    
    result += change / coin;
    // 잔돈에서 차감
    change %= coin;
}