▶ Heaps

Recall Priority Queue ADT

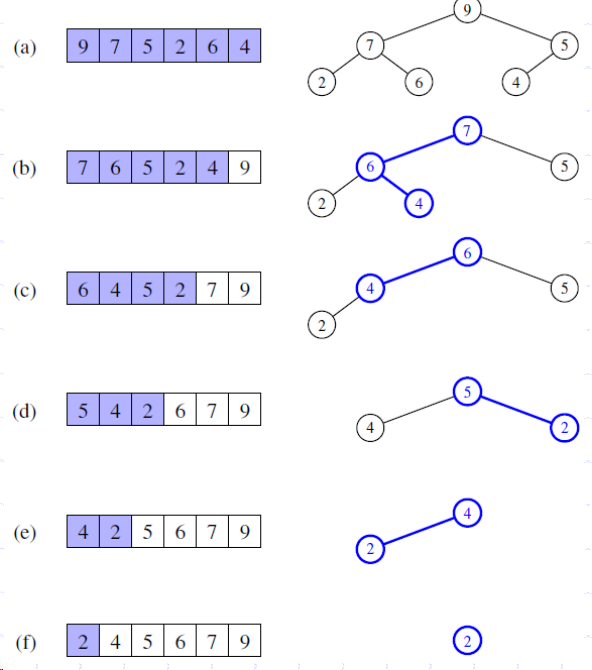
Recall PQ Sorting

Selection 정렬 - unsorted list 기반의 PQ 구현

1) 시퀀스 내용을 정렬하지 않고 그대로 PQ 배열에 카피후,
2) 최솟값을 일일이 맨 앞에서부터 비교하면서 찾아내고, 찾아낸 최솟값을 PQ 에서 추출하여 시퀀스에 옮김
3) 시퀀스에는 점차적으로 차곡차곡 오름차순으로 정렬된 결과가 쌓일것임

• PQ를 unsorted list(unsorted 배열) 로 구현했을때의 실행시간
  insert( ) : O(1) => n번 진행하면 O(n)
• 시퀀스의 원소들을 정렬하지 않고 PQ 배열에다 들어오는 대로 차곡차곡 쌓는다.
  (단순히 시퀀스 원본을 그냥 배열에다 그대로 카피하는 것이다)
• 배열 맨 끝에다 시퀀스에서 건져온 새로운 원소 삽입하면 끝이므로 O(1)
• 하나의 원소를 insert 하는 것이 O(1) 이므로 n개의 원소를 진행하면 O(n)

• removeMin( ) , min( ) : O(n) => n번 진행하면 O(n^2)
  정렬안된 배열에서 최솟값을 찾는 과정 : O(n)
• 맨 처음 원소는 비교를 n-1번 진행
  arrayMax 수도코드처럼 currentMin <- arr[0] 해놓고 for문을 돌린다.
• 2번째 원소는 (n-2)번, 3번째 원소는 (n-3)번, ... 마지막 원소는 1번 진행
  1 + 2 + 3 + ... + (n-2) + (n-1) = O(n^2)
  (O(n)이 n번 필요하다고 생각해도 됨)

2. Insertion 정렬 - sorted list 기반의 PQ 구현

1) 시퀀스에서 하나하나 원소를 PQ 배열에 집어넣을 때마다 계속 정렬된 상태를 유지.
2) 정렬이 완료되면 시퀀스에 PQ 내용을 카피

• insert( ) : O(n) => n번 진행하면 O(n^2)
  새로운 원소가 들어오면 자신이 정렬될 적절한 위치를 찾아감

• 정렬된 시퀀스에서 맨뒤의 원소 부터 시작해서 값을 비교해나가며 자리를 바꿔가며 자신이 위치할 곳을 찾아냄
  최악의 경우 : O(n)

• 내가 minimum value 일때
  내가 최솟값이면 계속 앞으로 나아가면서 총 n번 비교해야함
  insert연산을 총 n번 진행하면 1 + 2 + 3 + ... + (n-1) = O(n^2)

• O(n) 을 n번 진행한다고 생각해도 됨
  cf) Best case : 내가 최댓값일때
  ( 최초 비교시, 내가 앞 원소 값보다 크면 1번 비교하고 끝임 )

• removeMin( ), min( ) : O(1) => n번 진행하면 O(n)
• PQ 에서 정렬이 끝난후 다시 시퀀스에 옮기는 과정(copy 하는 과정) : O(n)
  removeMin : PQ의 맨 앞 원소를 삭제하는 행위가 곧 최솟값을 삭제하는 행위이다.

Heaps

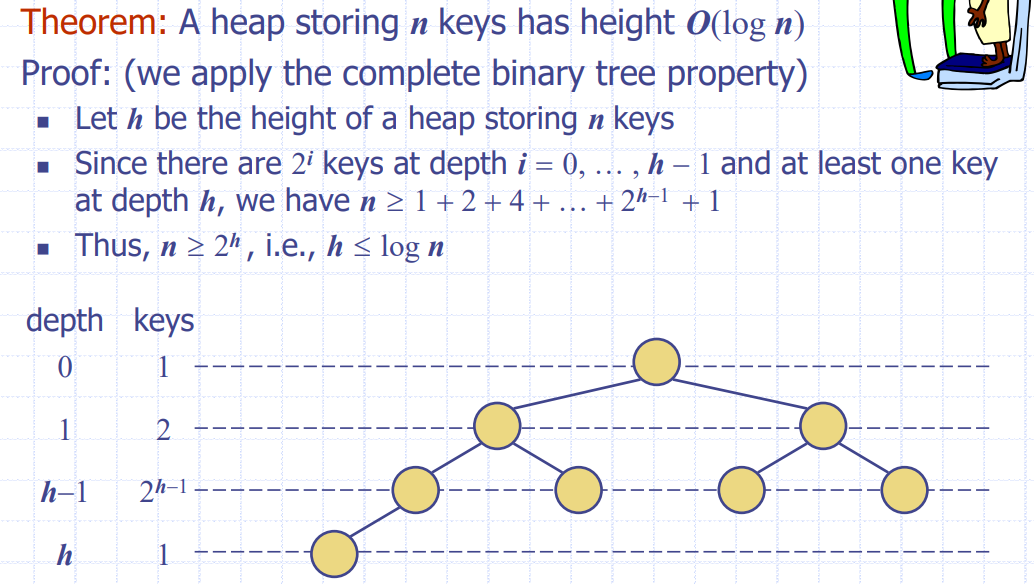
Height of Heap

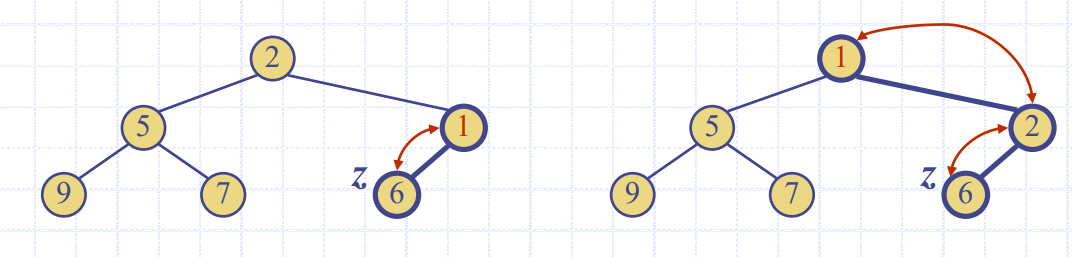
Insertion into a Heap

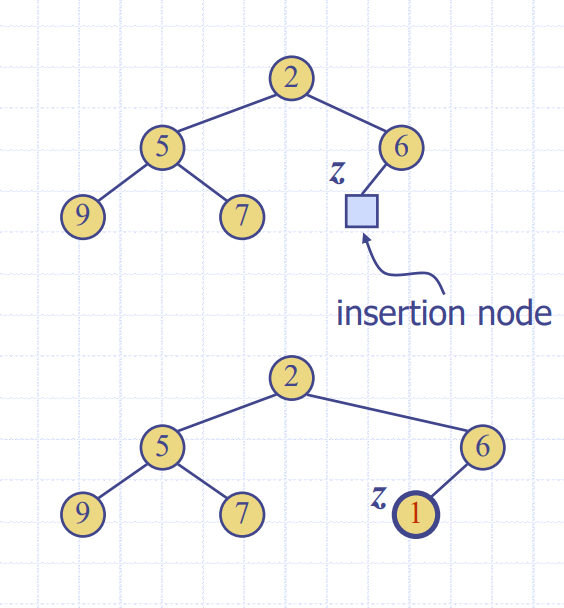
• 자식 노드는 부모노드보다 커야하므로 UPHEAP해야 함.

Upheap

• upheap은 높이만큼 진행되므로 O(logn)의 시간복잡도를 가짐
  

Removal from a Heap

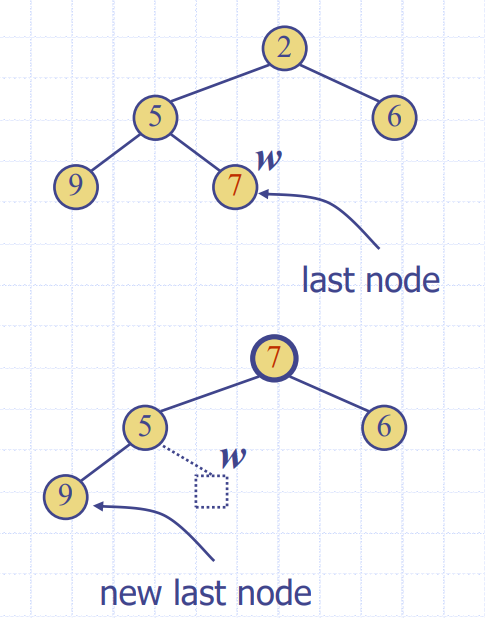
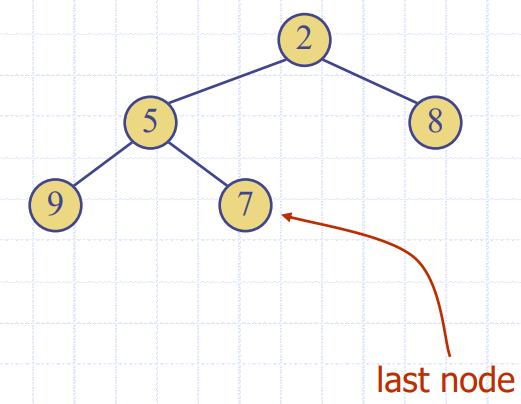
• 제일 작은 놈이 맨 위에 있다는 건 당연함. 그러나 제일 작은 놈을 remove하면 tree구조가 깨져버림
• 그렇기에 제일 작은 놈과 last node를 바궈치기 한 후 DOWNHEAP 진행

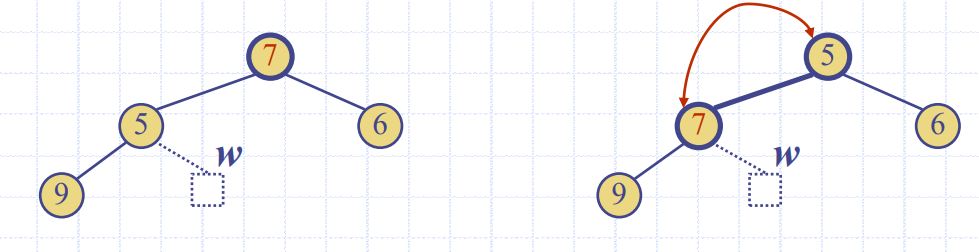
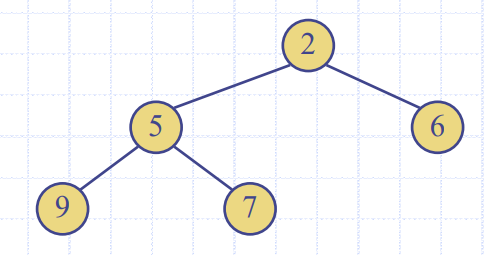
Downheap

• downheap 역시 높이만큼 교환이 일어지므로 시간복잡도 O(logn)
  

Array-based Heap Implementation

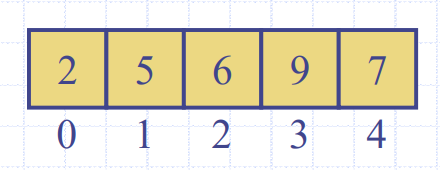
Python Heap Implementation

Merging Two Heaps

• 추가 원소를 받아서 root에 넣고, DOWNHEAP 호출
• O(logn)의 시간 복잡도를 가짐
  
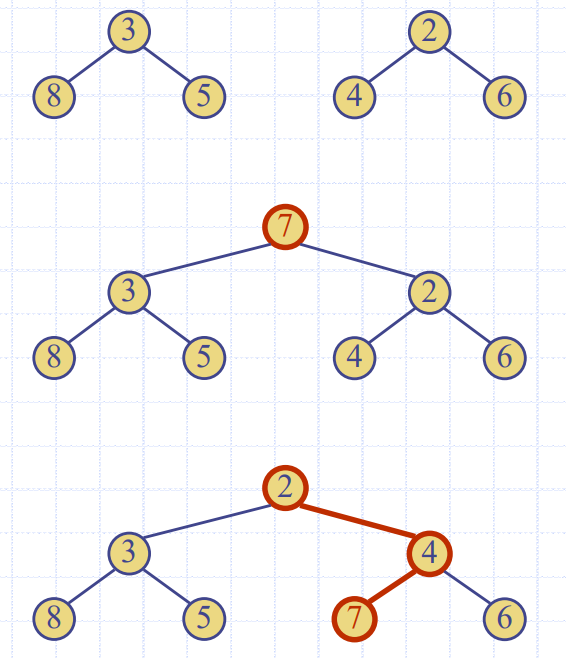
• 조건

1. 두 힙이 모두 꽉 차 있어야 함.

Bottom up Heap Construction

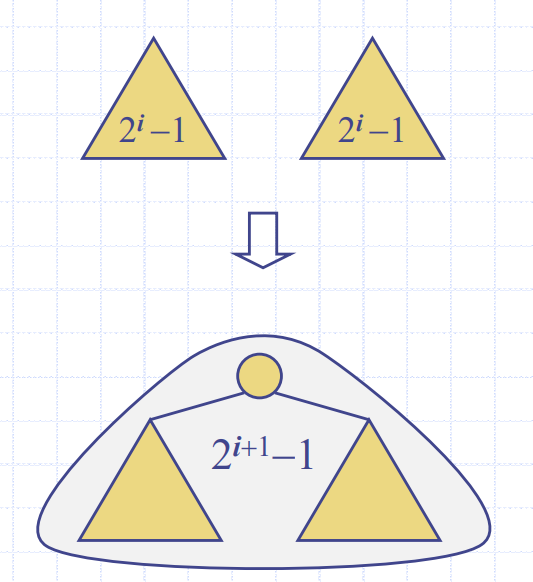
• 랜덤하게 맨 아래 층 노드를 뽑아서 채움
• 그 후 랜덤하게 맨 아래 -1 층 노드를 뽑아서 채움
• downheap호출해서 망가진 트리 구조 수선
• 그 후 새로 부모 랜덤 배정 후 downheap
• ....

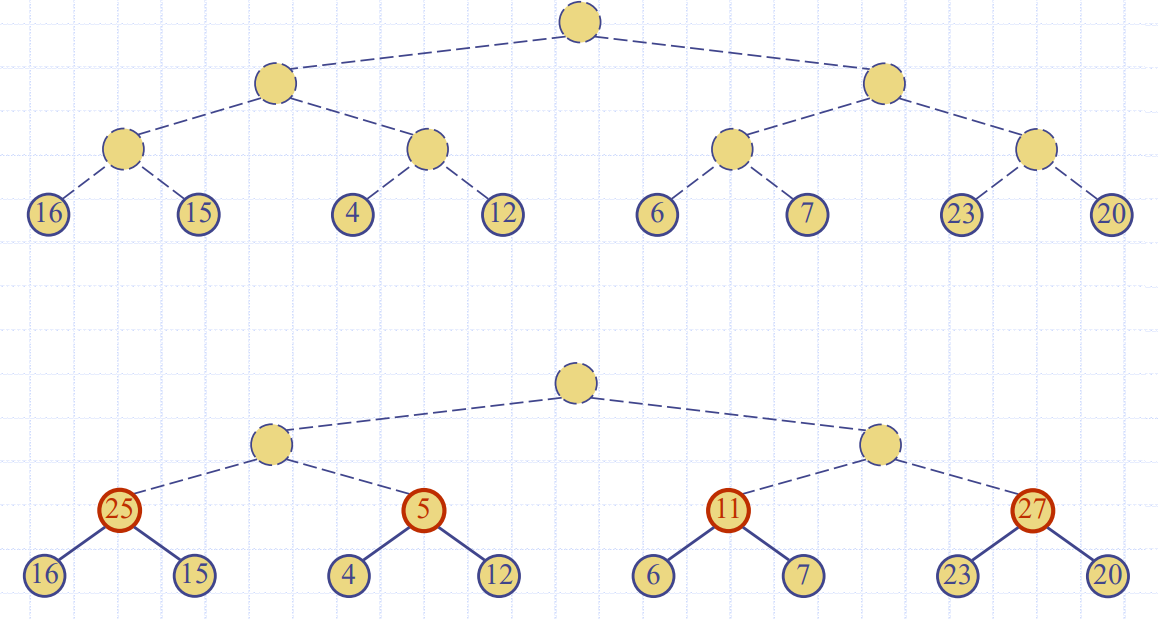
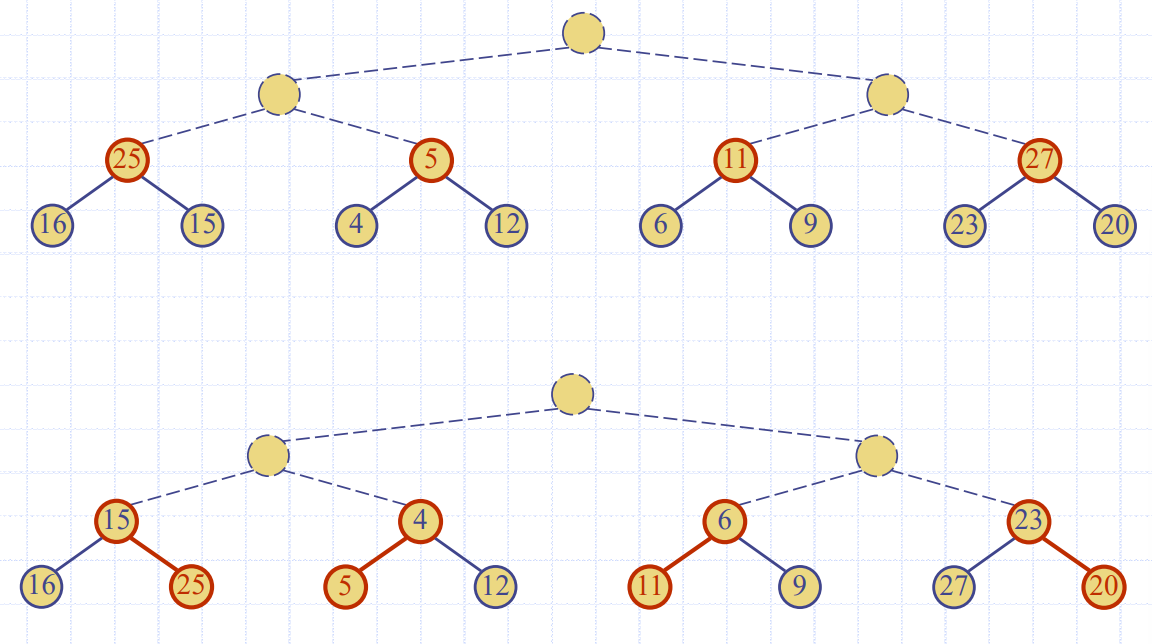
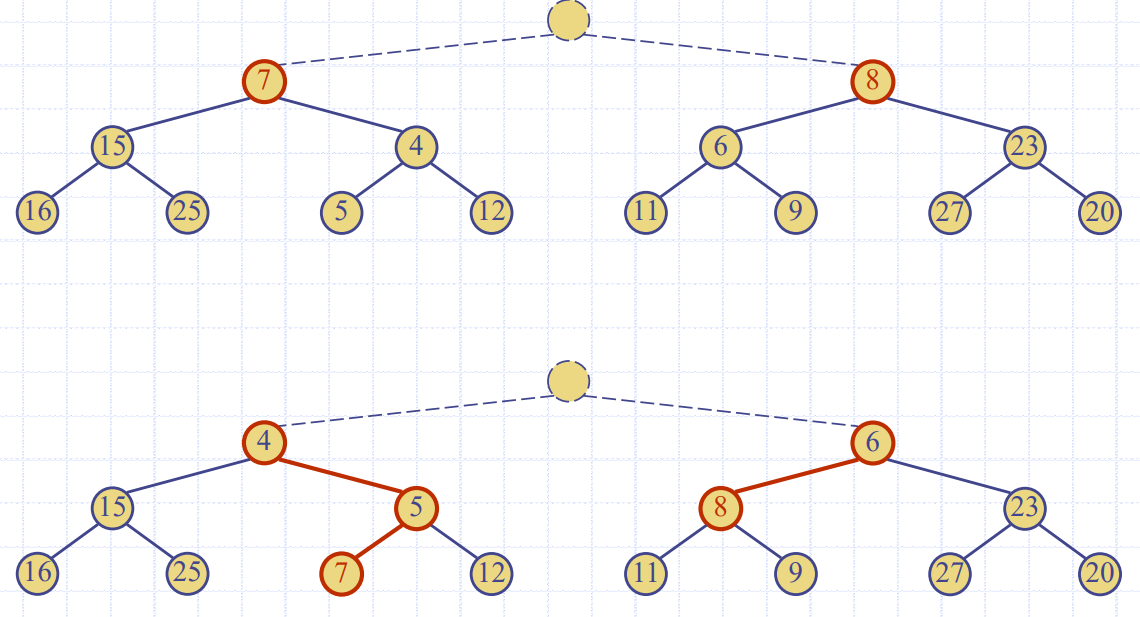
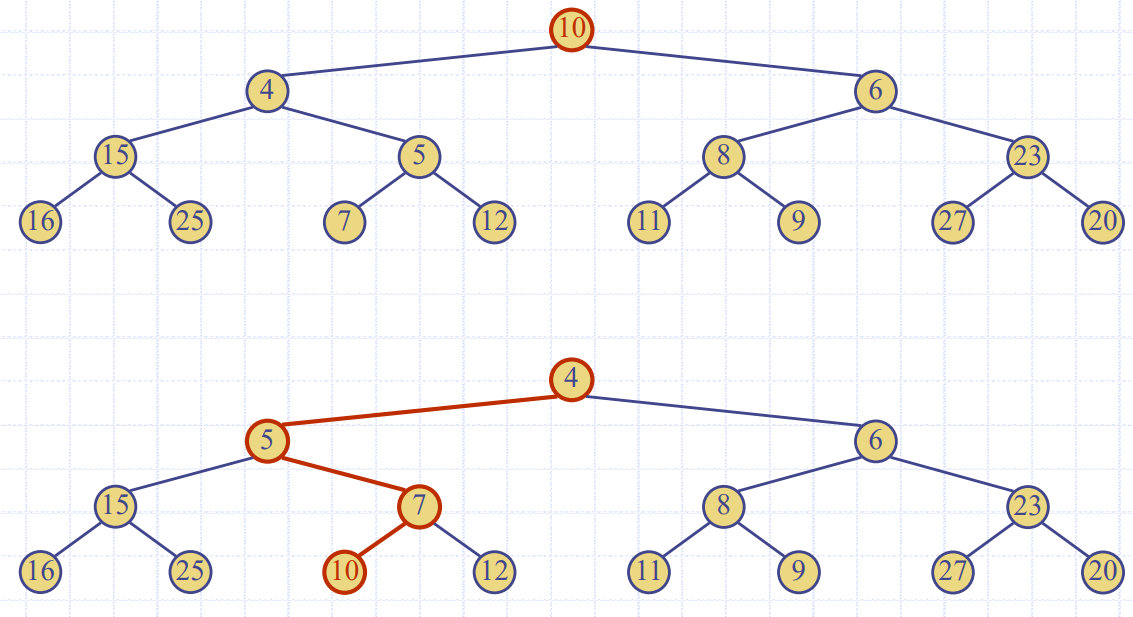
Analysis of Heap Construction

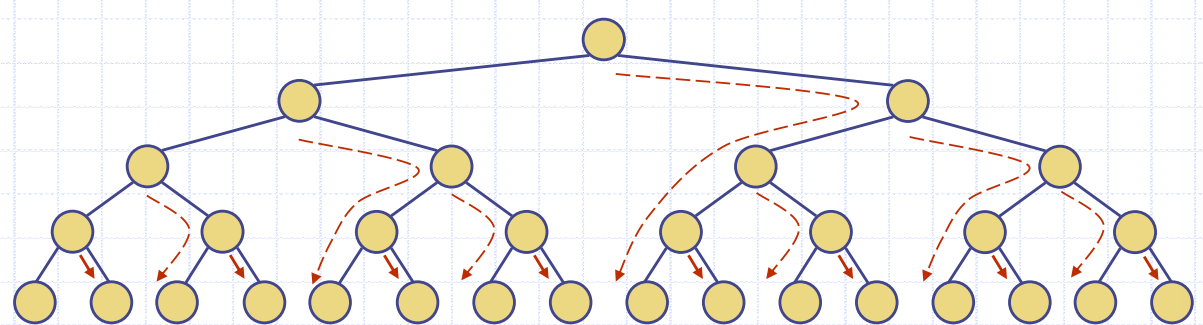
• heap 구조는 당연히 아래 계층에서 노드가 위 계층 노드보다 많으므로, 아래 계층에서의 계산을 최대한 회피해야 함.
• 그래서 DOWNHEAP을 사용하는 bottom up heap은 UPHEAP을 사용하는 일반적인 방법보다 시간 복잡도가 적음 O(n)

O(n)에 대한 이유 설명이 필요하다면
https://velog.io/@msung99/%ED%9E%992

• 위 그림은 모든 노드가 최악의 경우로 내려가는 경우
• 각 노드는 맨 처음 오른쪽으로 내려가고 그 다음부터 왼쪽으로 내려가는 것으로 가정
• 모든 경우에 최악의 경우가 발생했는데, 빨간 선이 겹친 것이 없음.
• 각 빨간 선마다 한번 씩 내려가는데 비교 연산을 2번씩 진행하고 내려감
• 즉, 빨간 선마다 비교 연산을 2번하고, 그 외에는 비교 연산을 하지 않음.
• 즉 비교 연산의 총 횟수 = 빨간 간선의 수 x2
• 그러나 빨간 간선의 수는 총 edge의 수보다 작거나 같음
• 그러므로 빨간 간선의 개수는 전체 간선(edge)의 수보다 항상 작으므로
• 비교연산 횟수 <= 2n
• 이에 따라 비교연산 횟수 <= O(n)

Heap Sort