▶ Tree

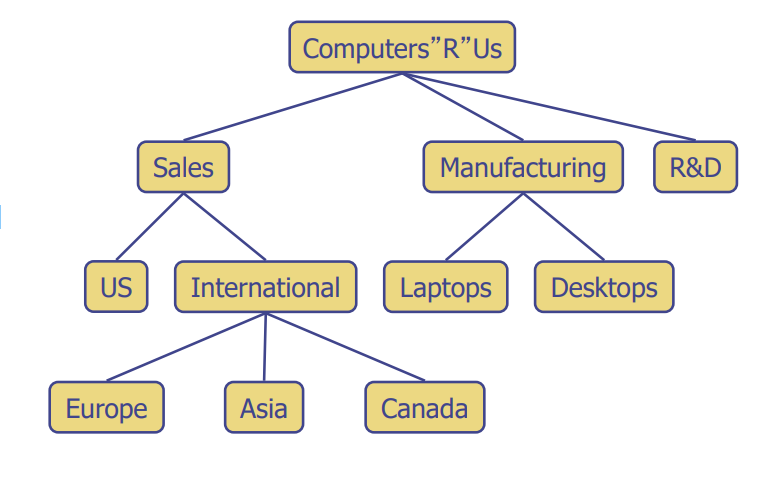
• 데이터의 위계 구조를 나타낼 때 사용
• tree는 parent-child node가 존재
• ex. Organization charts, File systems, Programming environments

Ex. File System

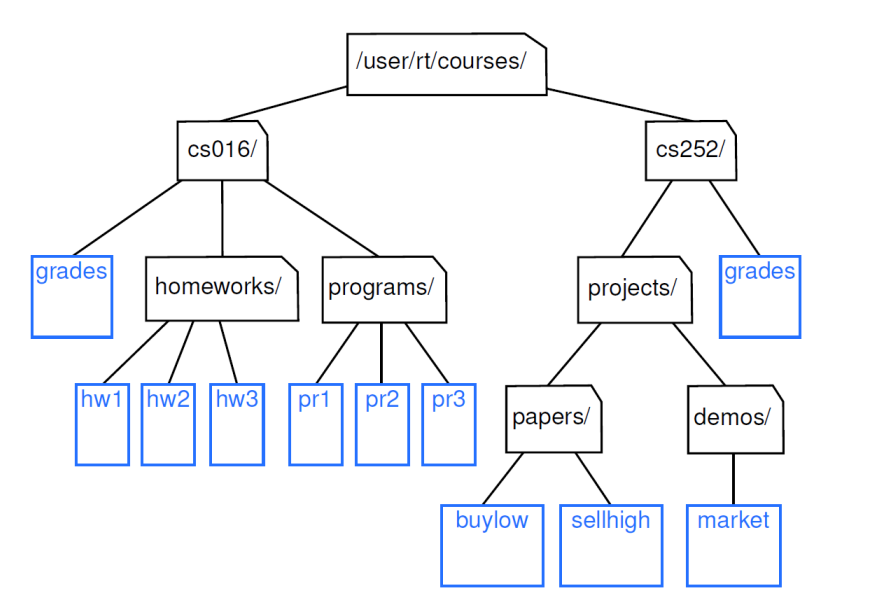
Tree Terminology

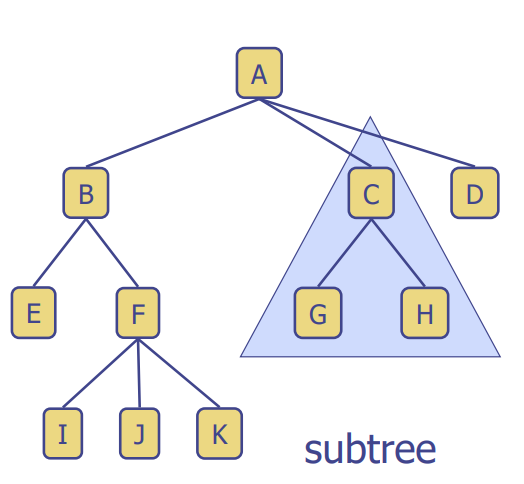
Root

: 부모가 없는 노드 A

Internal node

: 최소 1명 이상의 자식이 있는 노드
: A,B,C,F

External node(aka leaf)

: 자식이 없는 노드
: E I J K G H D

Ancestors of a node

: 부모, 조부모, 등등
: parent, grandparent, grand-grand parent etc

Descendant of node

: 자식, 손주 등등
: child, grandchild, grand-grandchild

Subtree

: 노드와 그의 자식을 가지고 있는 노드

Tree ADT

Generic methods

• Integer len()
• Boolean is_empty()
• Iterator positions()
• Iterator iter()

Accessor methods

• position root()
• position parent(p)
• Iterator children(p)
• Interger num_children(p)

Query methods

• Boolean is_leaf(p)
• Boolean is_root(p)

Update method

• element replace(p, o)

Abstract Tree Class in Python

class Tree:

class Position:
	def element(self):
    	raise NotlmplementedError('must be implemented by subclass')
    def __eq__(self, other):
    	raise NotlmplementedError('must be implemented by subclass')
    def __ne__(self, other):
    	return not(self == other)
        .
        .
        .

Depth of a Node

: 가장 깊은 구간으로 측정

Height of a Tree

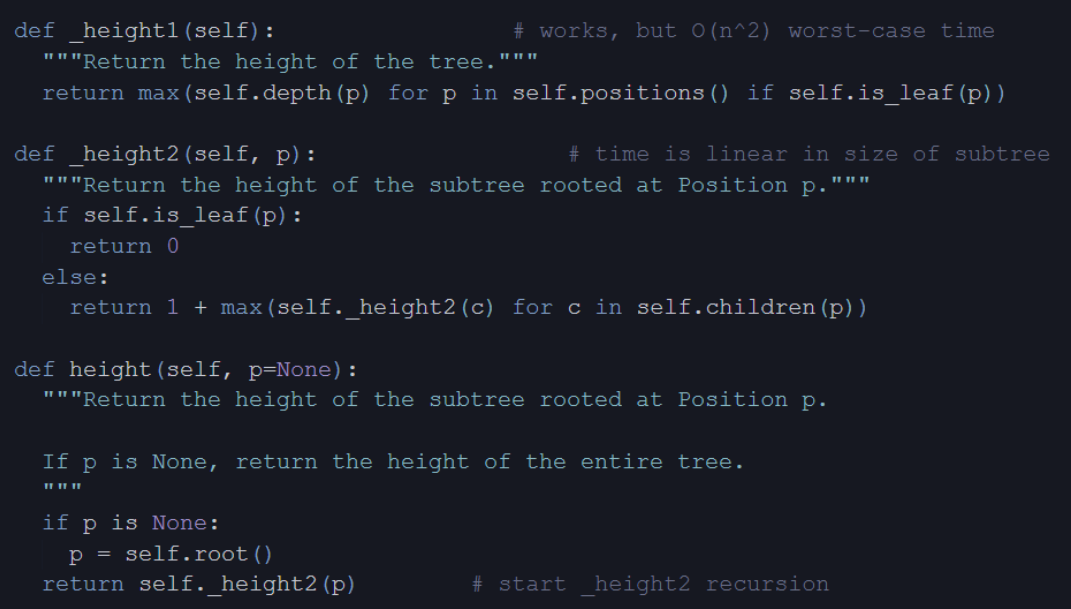
Binary Trees

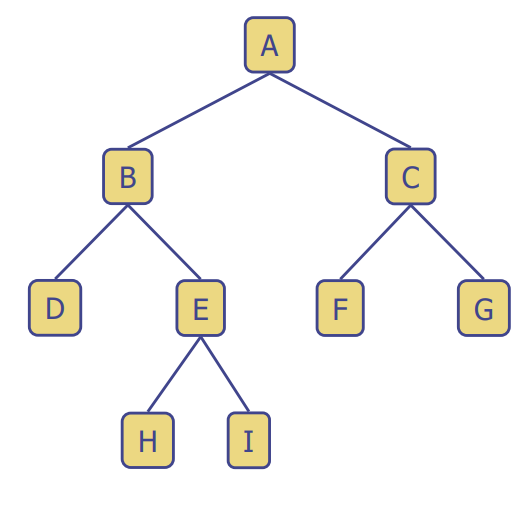
• 조건1) 각 노드가 최대 2명
  : 모든 node의 자식이 0 or 2명이라면 full binary tree라고 부름
• 조건2) 자식끼리도 우선순위가 있어야함(ex. 왼쪽이 형, 오른쪽이 동생)
  : left child, right child
• ex. arithmetic expressions, decision processes, searching

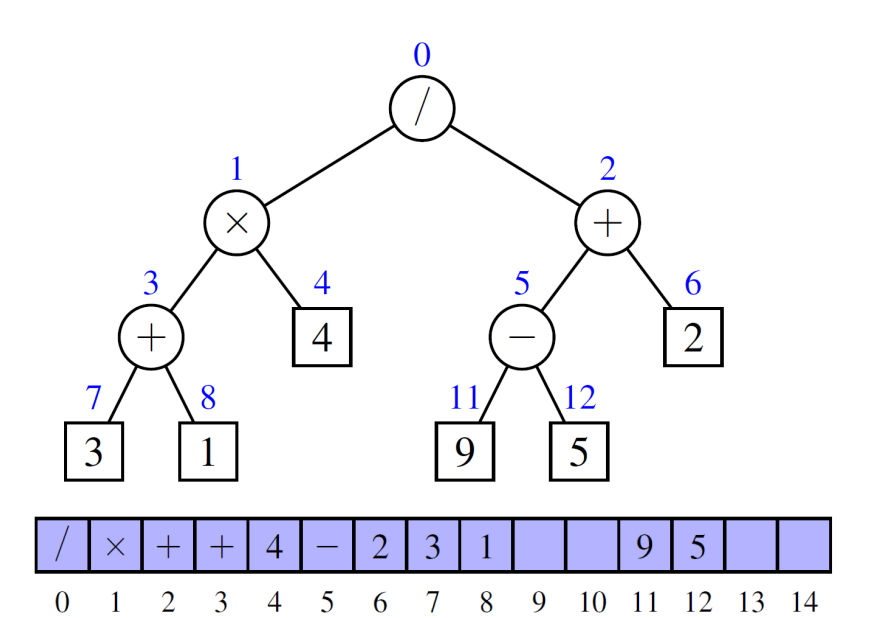
Ex. Arithmetic Expression Tree(연산자 트리)

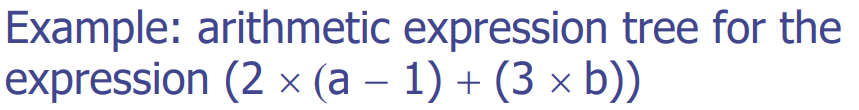
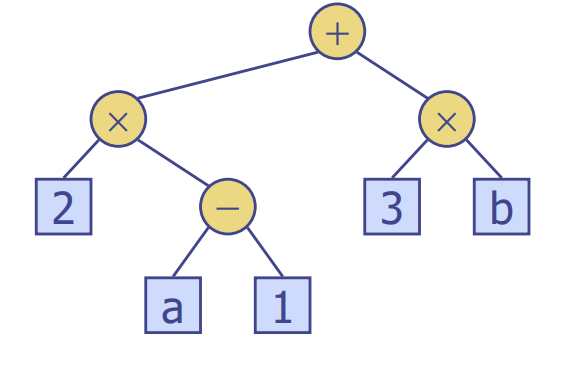
• internal nodes: operators(연산자)
• external nodes: operands(숫자)

Ex. Decision Tree

• internal nodes: questions with yes/no answer
• external nodes: decisions
  

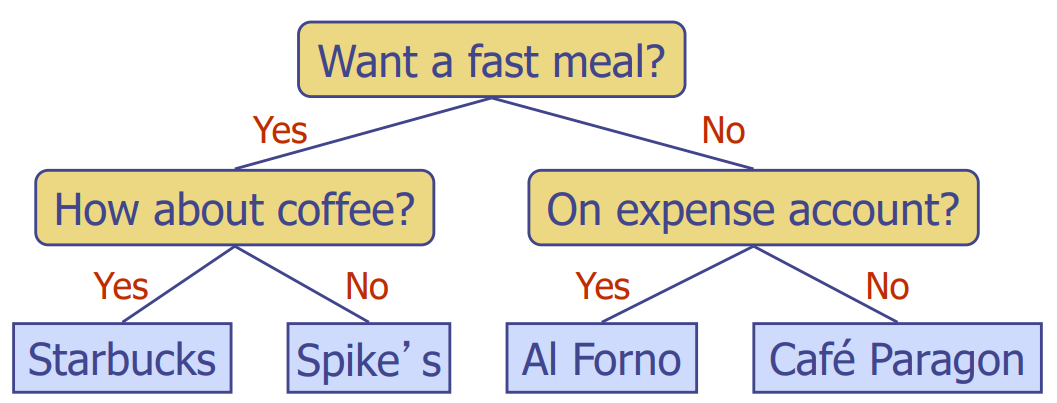
BinaryTree ADT

Additional methods

• position left(p)
• position right(p)
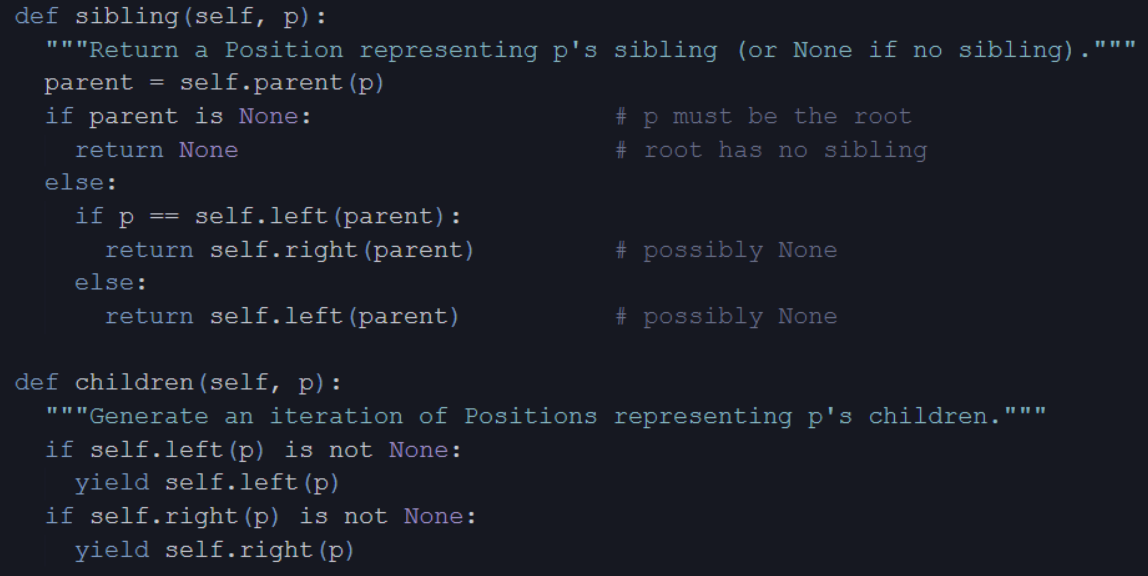
• position sibling(p)

Properties of Full Binary Trees

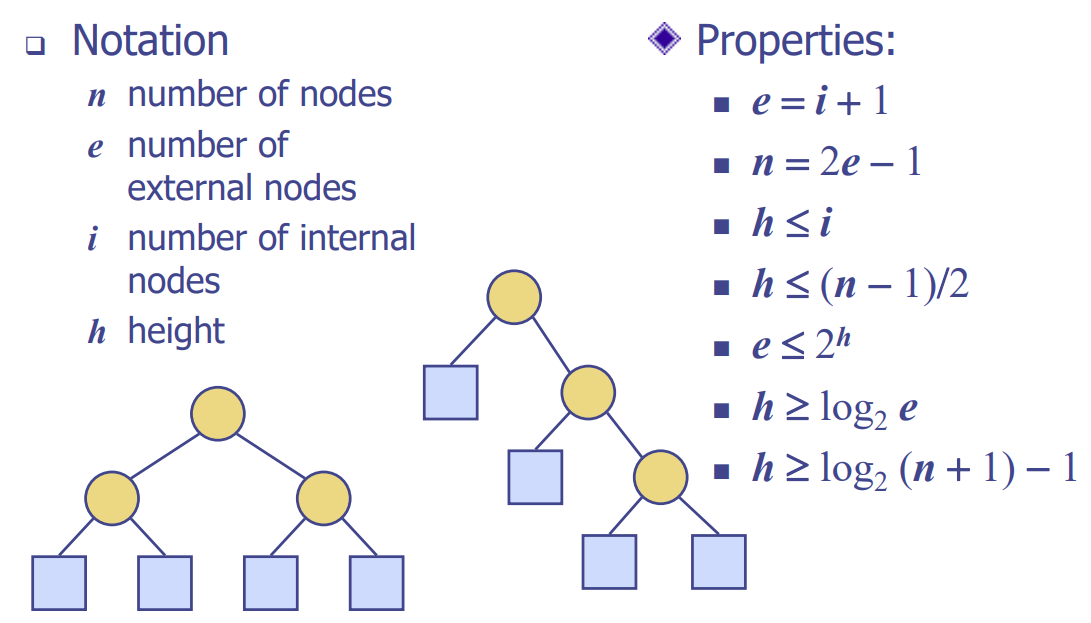
• ex. depth
  : 우측 트리의 depth는 2
  : 좌측 트리의 depth는 3

Linked Structure for Binary Trees

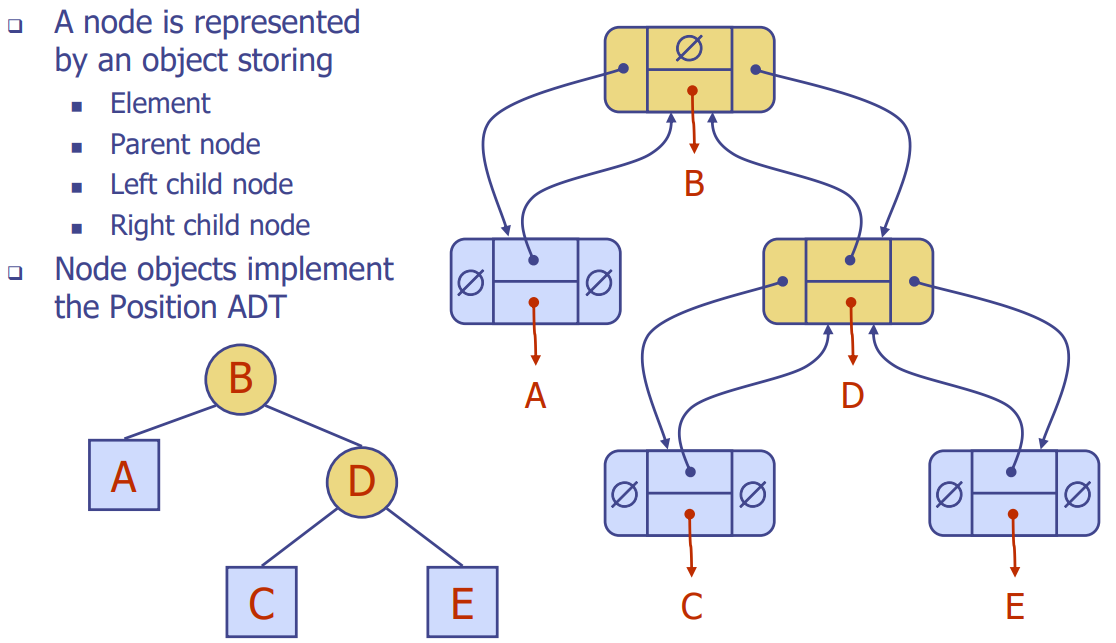
• 자기 노드 포인터 1개
• 부모님 가리키는 포인터 1개
• 왼쪽 자식 포인터 1개
• 오른쪽 자식 포인터 1개

Linked Binary Tree in Python

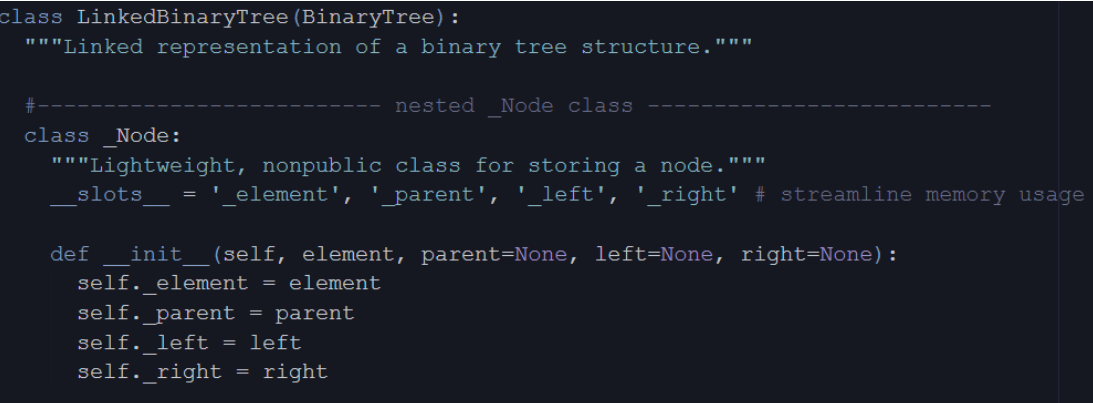
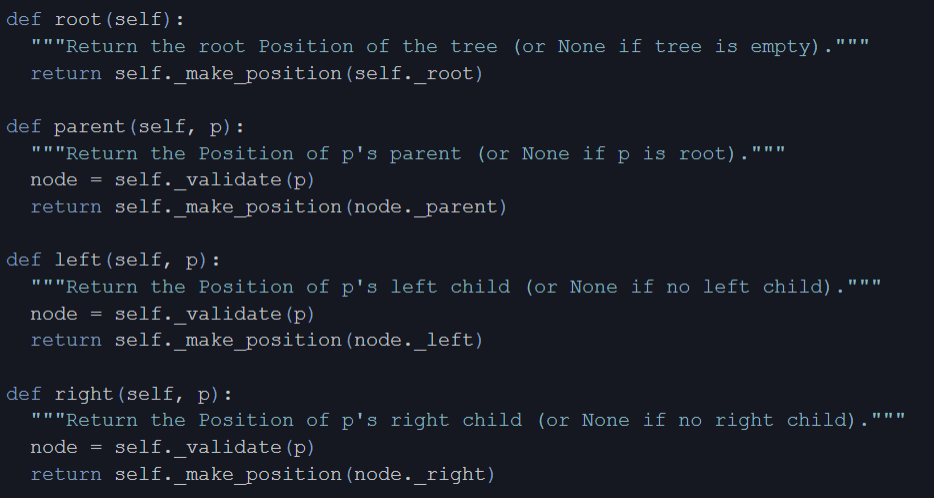
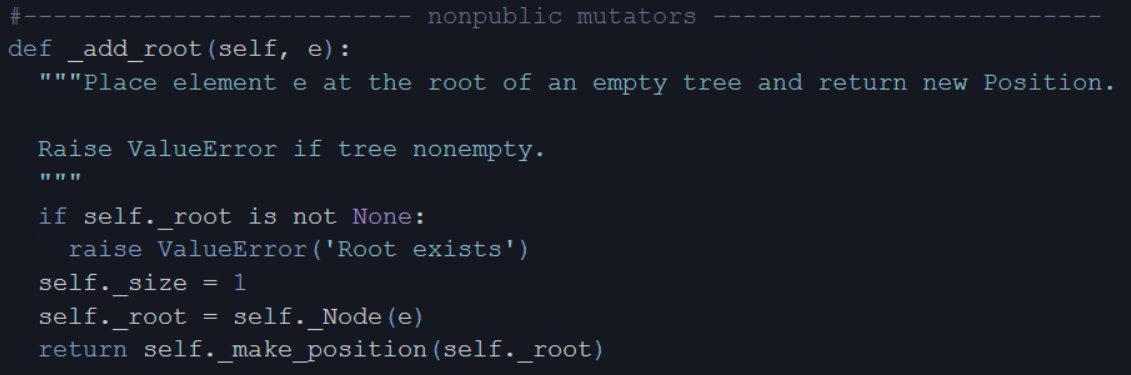
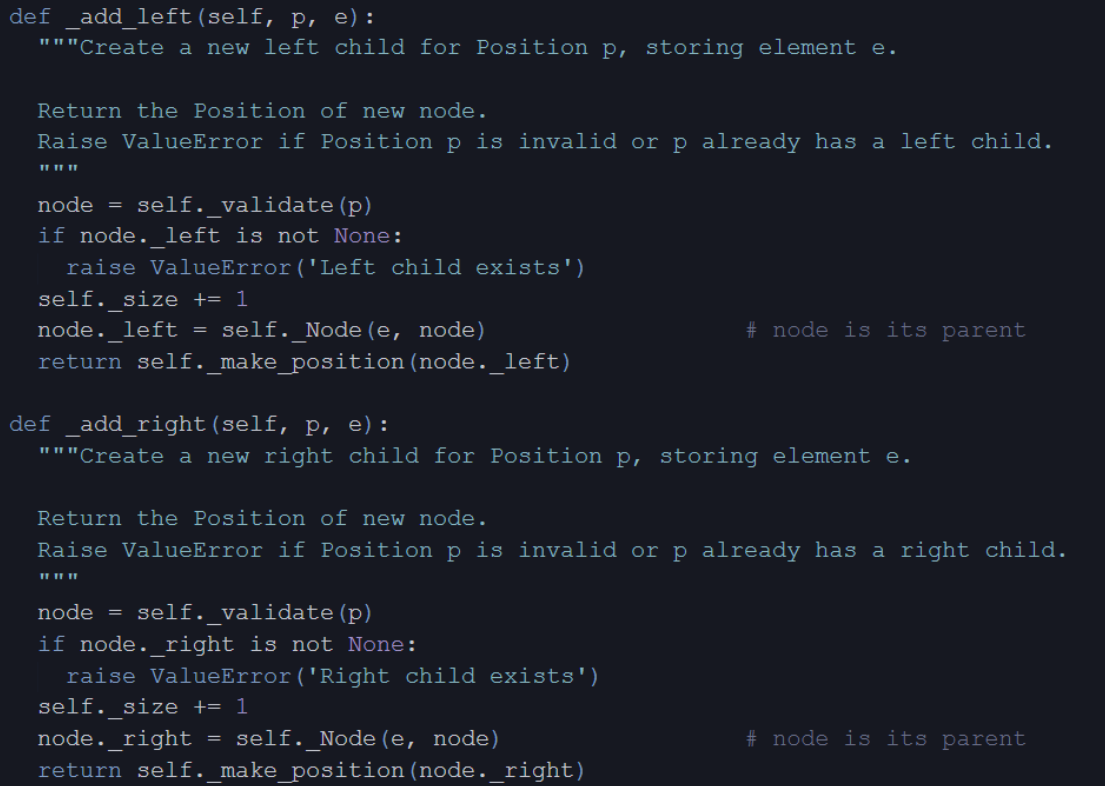
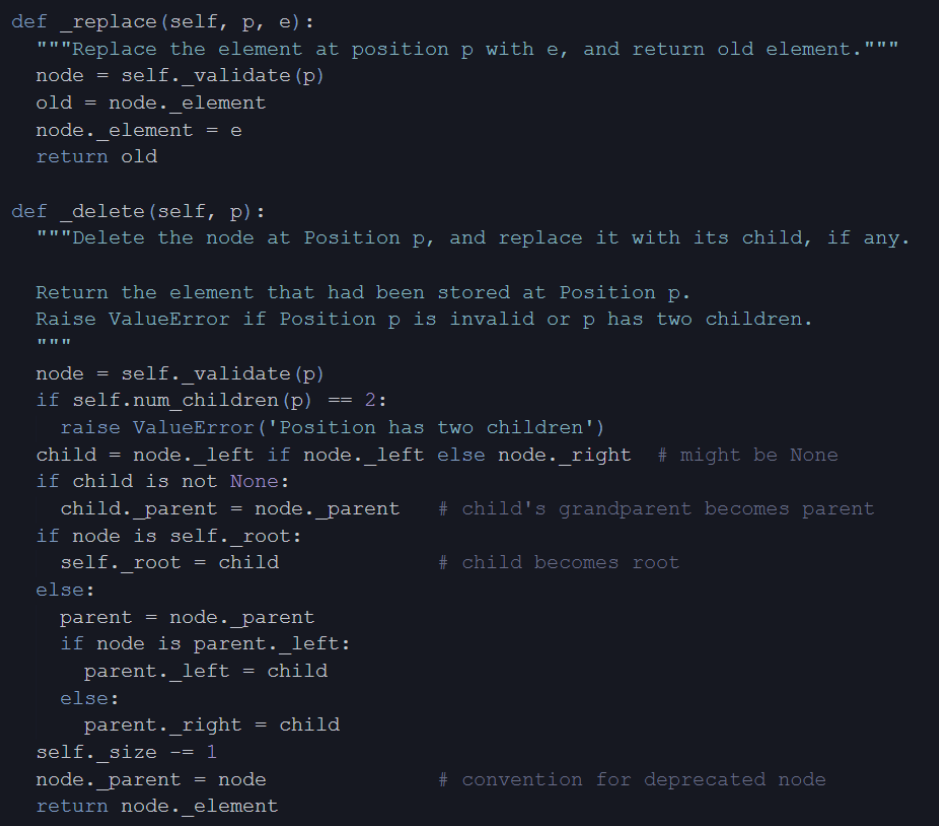
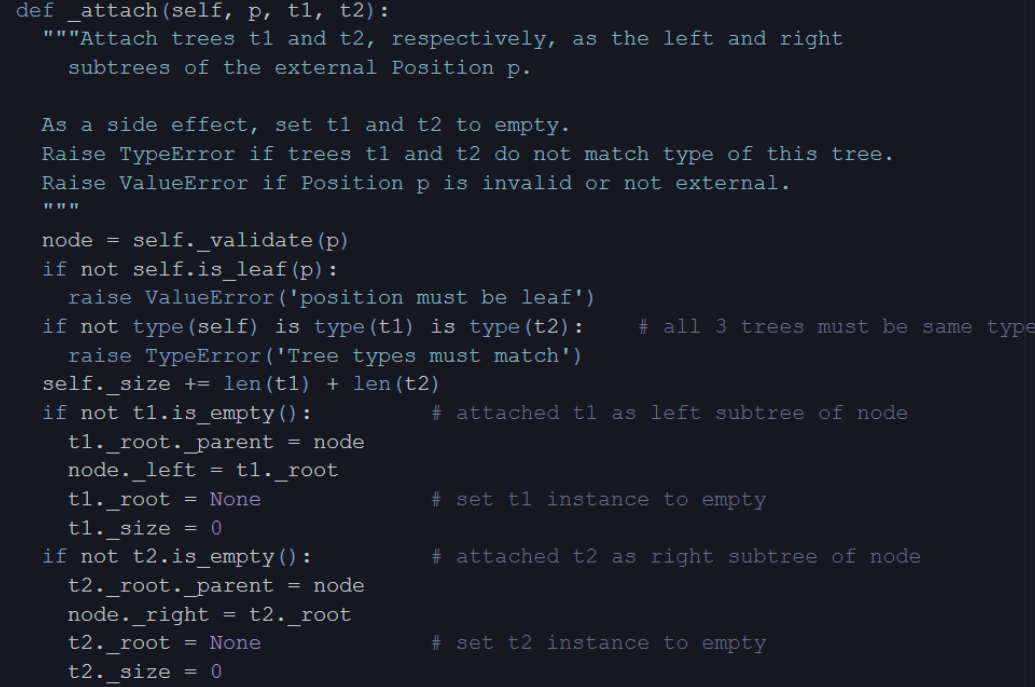
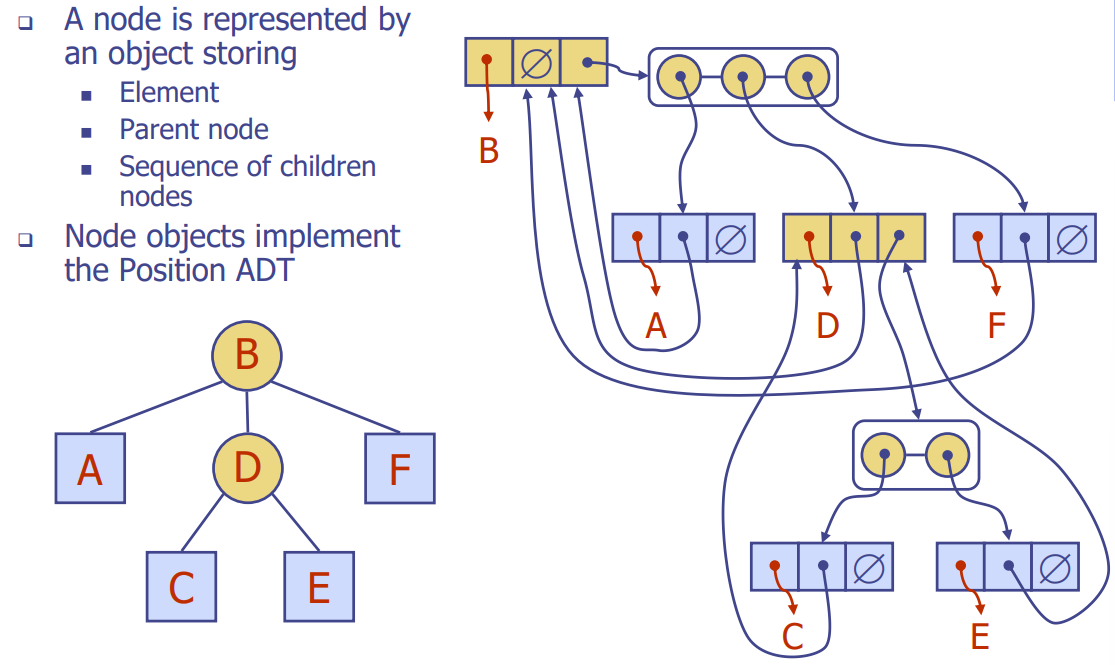
Linked Structure for Trees

Array-Based Representation of Binary Trees

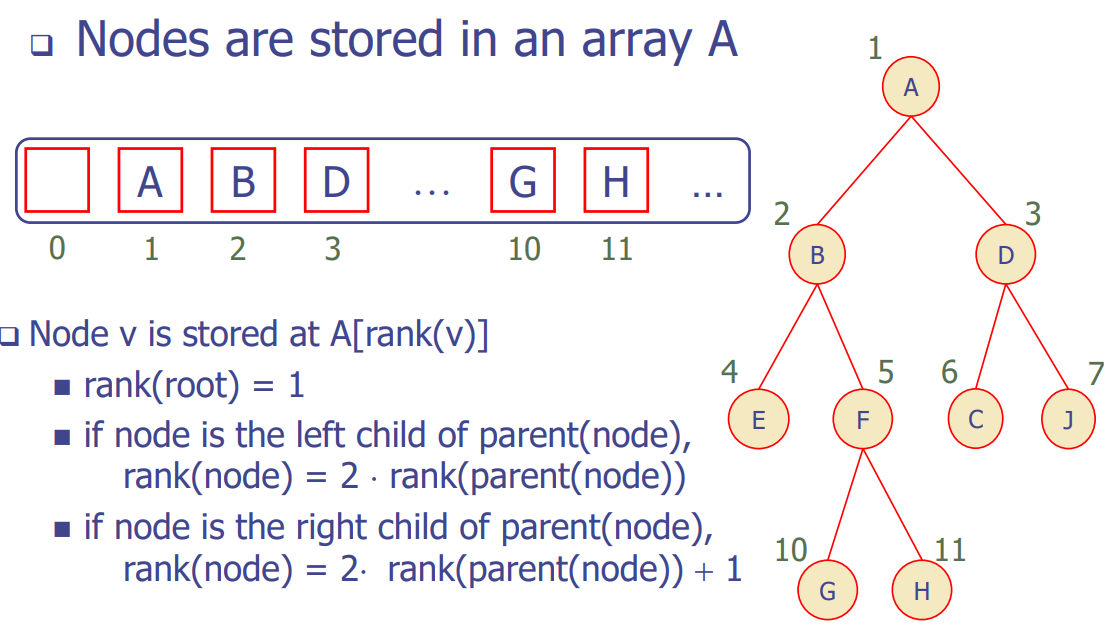
Array-Based Binary Tree

Preorder Traversal(전위순회)

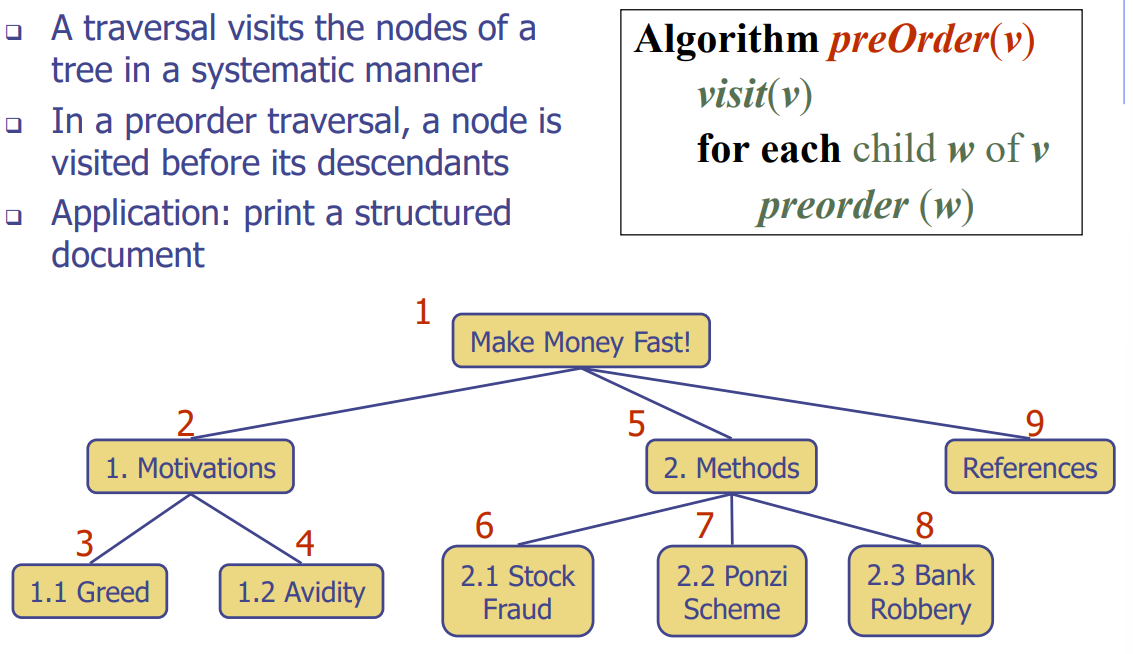
• 노드를 먼저 방문하고 왼쪽 끝까지 내려간 다음 오른쪽으로 이동하여 다시 시작하거나 오른쪽으로 이동하여 순회를 계속함.

Postorder Traversal(후위순회)

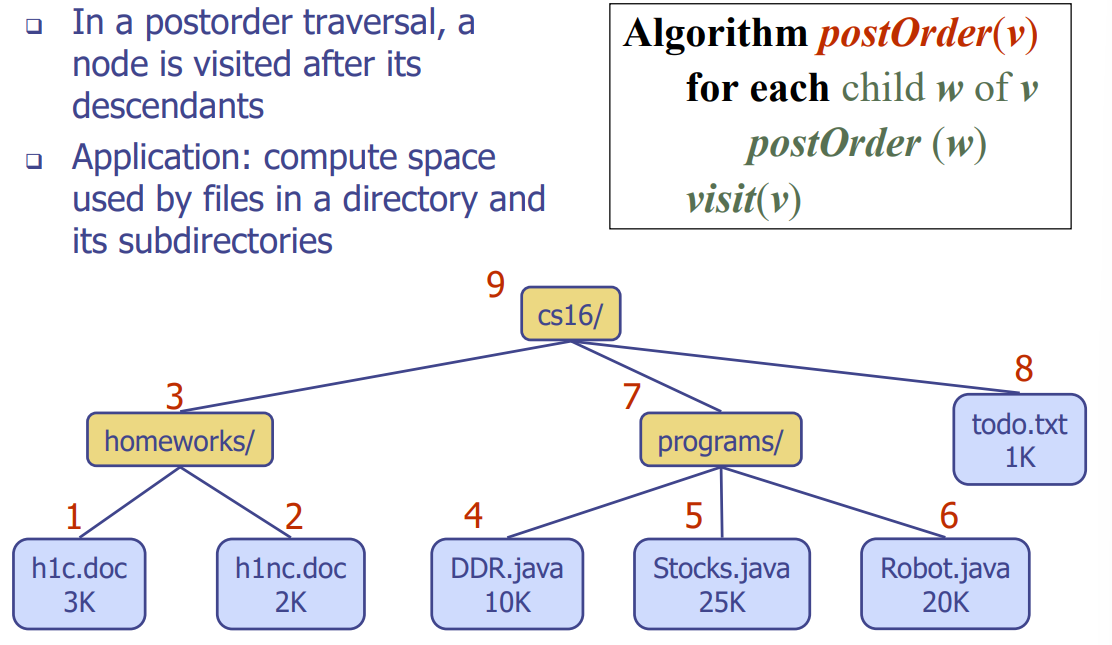
• 왼쪽 서브트리를 후위 순회한 후 오른쪽 서브 트리를 후위 순회. 그 후 노드 방문

Breadth First Tree Traversal

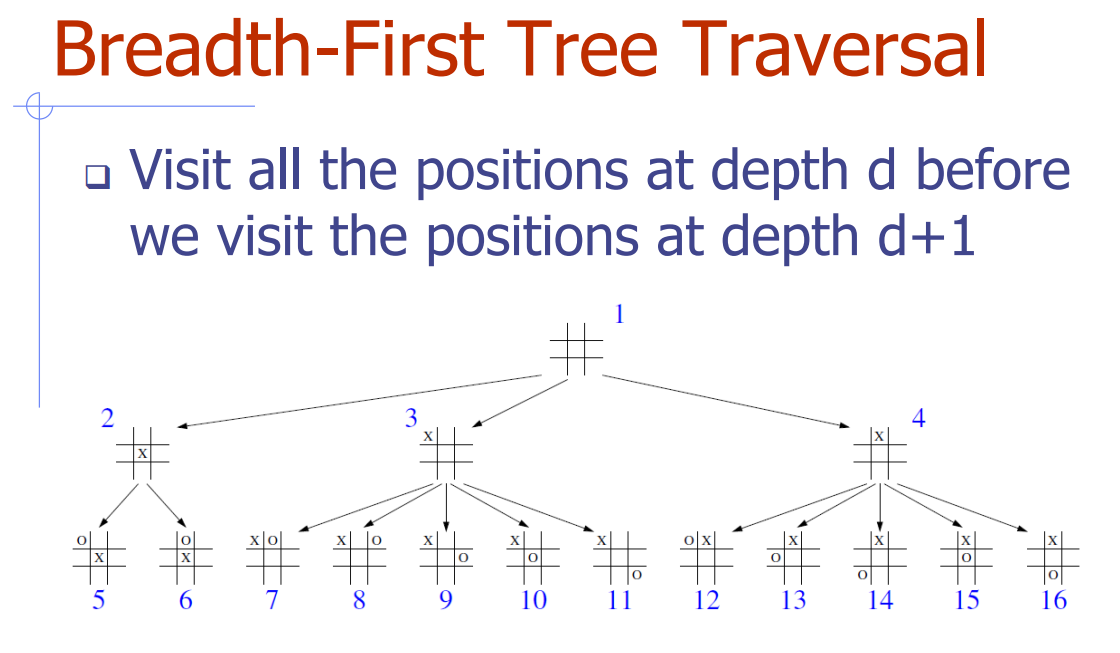
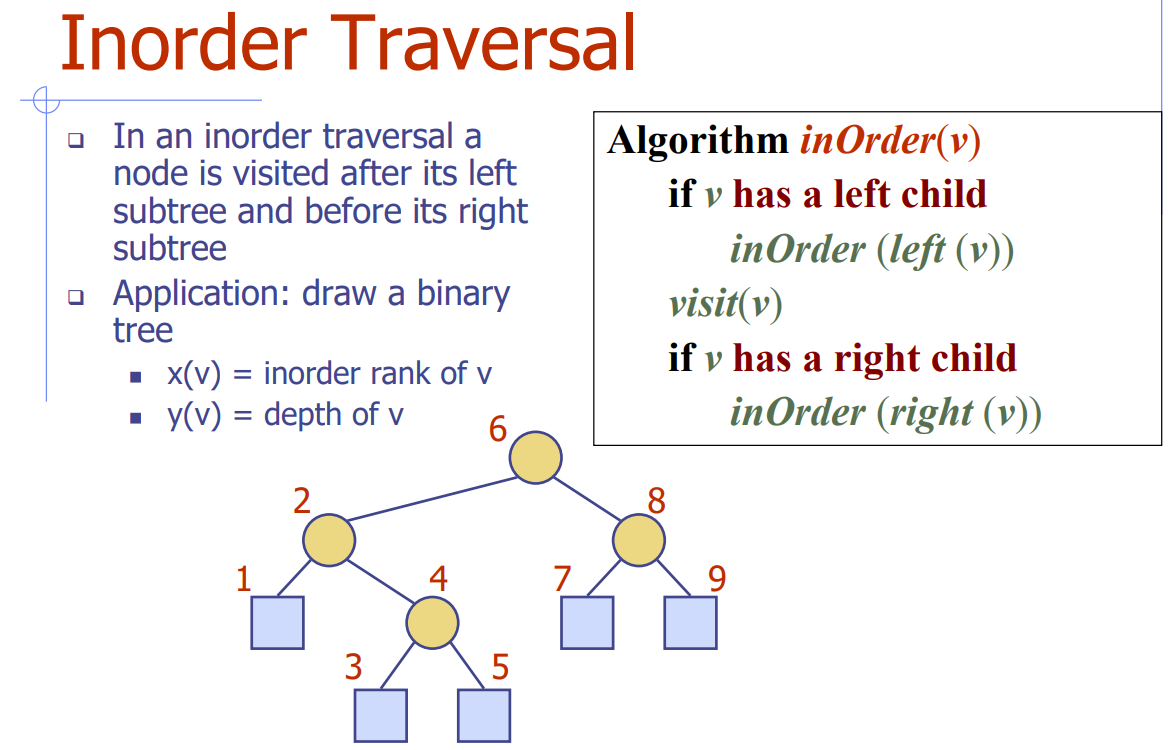
Inorder Traversal

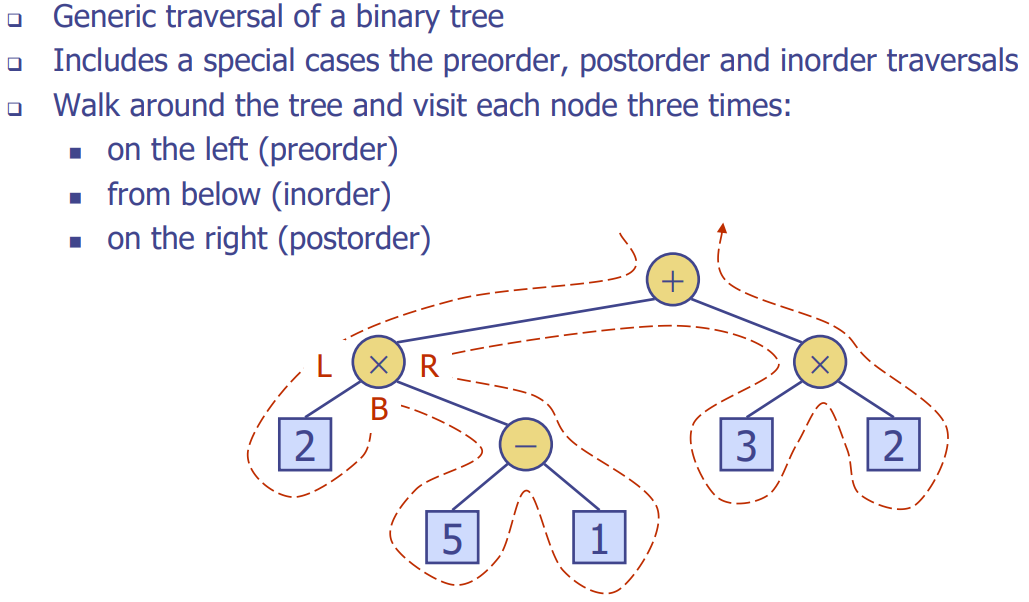
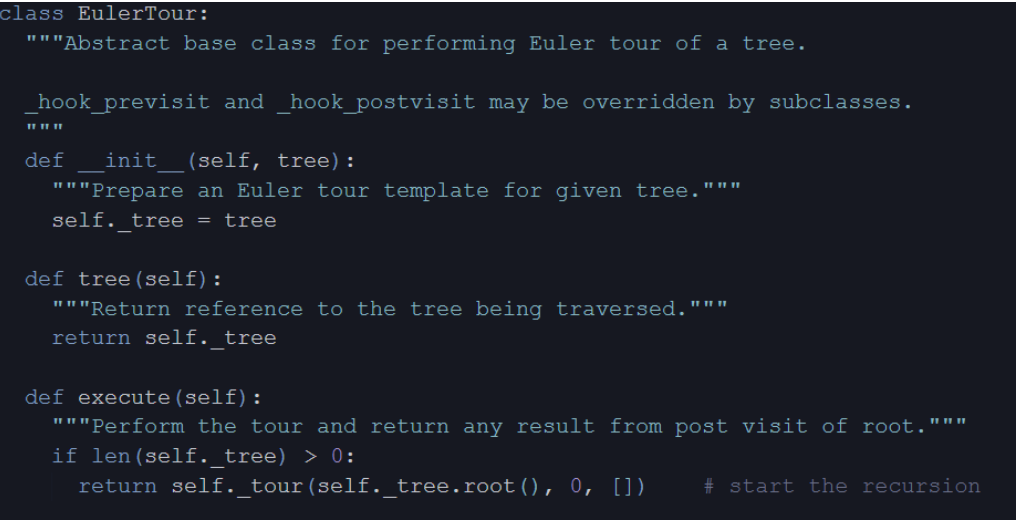
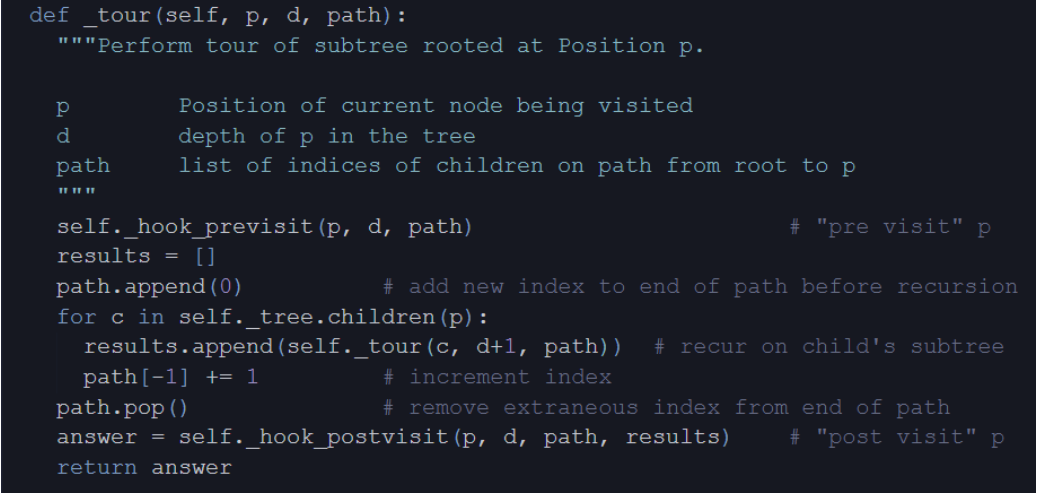
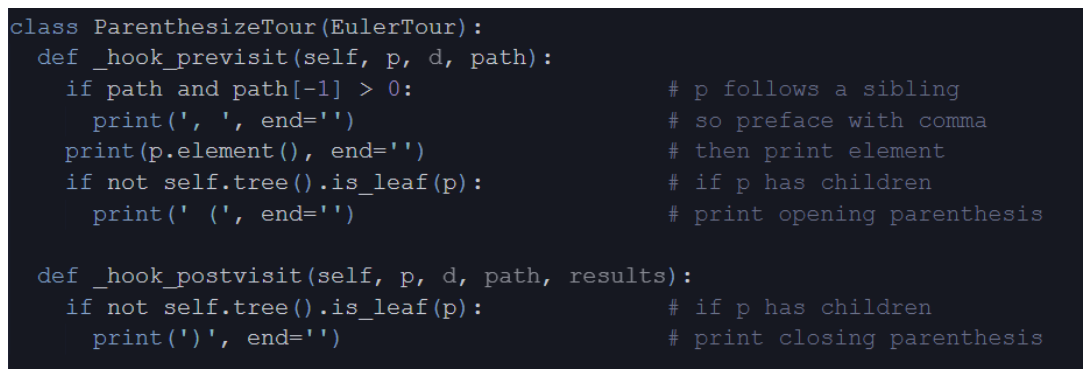
Euler Tour Traversal

• 전위, 중위, 후위 순회를 모두 합친 형태
• 방문 순서

1. 현재 노드
2. 왼쪽child
3. 현재노드
4. 오른쪽child
5. 현재 노드

Disk Space Tour