✨SOTA (state-of-the-art) 를 달성했던 DenseNet
당시 CNN 모델들은 점점 깊어지고(deeper), 정확해지고(accurate), 효율적으로 훈련할 수 있었는데,
바로 Shorter Connection 을 포함해서였다.
Shorter connection: 특정 레이어의 입력을 후속 레이어로 직접 전달하는 connection
DenseNet은 각 레이어가 입력부터 출력까지 모든 이전 레이어와 직접 연결되어 있다!
즉, L(L+1)/2 개의 direct connection (등차수열 합 공식)
vanishing-gradient problem 완화, strengthen feature propagation, encourage feature reuse, 파라미터 수 감소의 장점들이 있다.
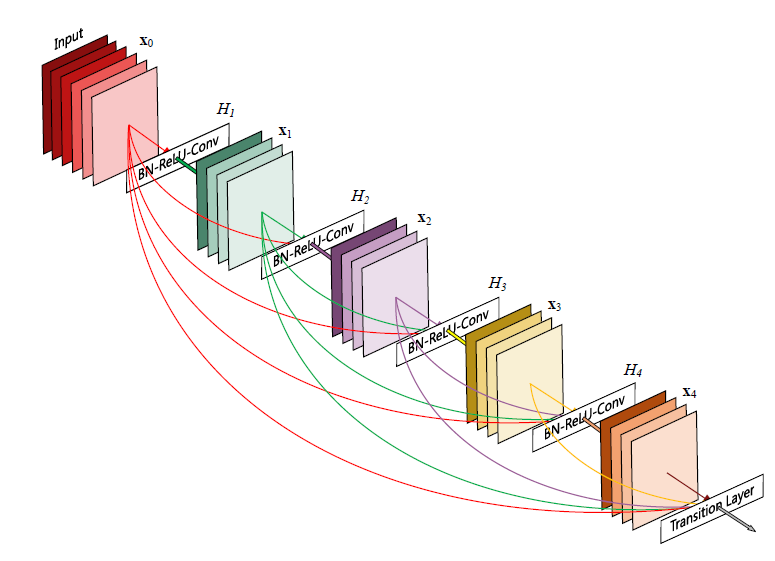
🍞1. Introduction
CNN(Convolutional neural network)은 dominant한 머신러닝 기법 중 하나로, 컴퓨터 하드웨어와 네트워크 구조의 발달로 더 깊은 CNN을 설계하고 학습할 수 있게 되었다.
특히 ResNet의 경우 100-layer의 장벽을 뛰어넘기도 했다.
하지만 CNN이 깊어질수록, input/gradient가 수많은 레이어들을 통과하면서 네트워크 끝으로 갈수록 그 정보가 소실되는 문제가 대두되었다.
ResNet, Highway Networks, FractalNet 등이 이러한 문제를 해결하기 위해 short path를 도입했다.
they create short paths from early layers to later layers. (논문 내용 그대로)
이러한 아이디어를 바탕으로, DenseNet은 간단한 connectivity pattern을 제안한다.
네트워크의 레이어 간의 maximum information flow를 보장하기 위해서, 모든 레이어를 직접적으로, 서로 연결했다.
ResNet은 feature들이 레이어를 통과하기 전 summation을 통해 결합되지만,
DenseNet은 concatenation으로 feature들을 결합한다.
모든 layer들을 densely하게 연결하여 DenseNet이라 부른다.
DenseNet의 장점들은 아래와 같다.
-
Fewer parameters
- 불필요한 피처맵의 재학습 X -
Improved flow of information and graidents
- 각 레이어들이 loss function / original input signal's gradient에 직접적으로 접근 가능 (서로 연결되어 있으니까) -> Deep supervision
- Overfitting 방지로 Regularization 효과
🍞2. Related Work
DenseNet의 네트워크와 유사한 cascade structure는 1980년대부터 연구되었는데, 작은 데이터셋에만 효과적이고 적은 파라미터 개수(수백 개 정도)의 네트워크에만 적용할 수 있었다.
Highway Networks에서는 bypassing path를 통해 처음으로 100개가 넘는 layer를 효과적으로 학습한 구조다.
Stochastic depth는 1202-layer ResNet을 성공적으로 학습시키기 위해 제안된 방식인데,
훈련 중 레이어를 랜덤으로 drop하여 학습을 향상시키는 방식이다.
이를 통해 깊은 residual network에는 상당한 양의 Redundancy가 존재한다는 것을 보여준다.
등등 여러 관련 연구 설명이 있는데 그냥 한번 슥 읽어보면 될 것 같다.
🍞3. DenseNets
기존의 CNN은 n-1번째 레이어의 output을 n번째 layer의 input으로 연결한다. 식은 아래와 같다.
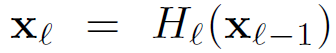
ResNet은 non-linear transformation을 bypass하는 skip connection을 추가한다.
gradient가 identity function을 통해 later lyer에서 earlier layer로 직접적으로 흐를 수 있는 장점이 있지만,
identity function과 H의 output이 summation을 통해 결합되기 때문에 information flow를 방해할 수도 있다.
식은 아래와 같다.
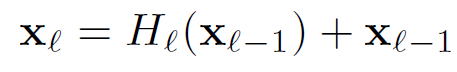
Dense Connectivity
DenseNet은 레이어 간의 information flow를 향상시키기 위해 어떤 레이어든 subsequent layer로 direct하게 연결하는 방식을 제안했다.

Dense Block -> Convolution + Pooling 의 반복 구조다.
n번째 레이어는 이전의 모든 레이어들의 피처맵을 input으로 받게 되는 것이다. 식은 아래와 같다.
x0, ... , xl-1 은 각 레이어에서 생성된 피처맵들의 concatenation이고, 이러한 dense connectivity로 인해 DenseNet이라는 이름이 붙었다.
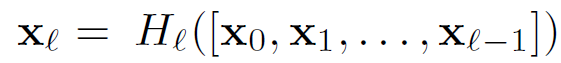
Composite Function
H는 BN(batch normalization), ReLU(Rectified linear unit), Conv(3 x 3 convolution)의 composite function으로 정의된다.
Pooling Layers
피처맵의 크기가 바뀌면 concatenation operation을 사용할 수 없다.
즉, down-sampling layer를 통해 피처맵의 사이즈를 바꿔주면 된다.
네트워크를 densly하게 연결된 dense block으로 나누고;
convolution과 pooling을 수행하는 레이어를 Transition layer라 한다.
Transition layer는 BN, 1x1 conv, 2x2 average pooling layer로 구성되어 있다.
Average Pooling?
보통 MaxPool을 많이 쓰는데, maxpool은 가장 큰 값을 선택함으로 특정 패턴이나 특성에 초점을 맞추고 그 외의 정보를 무시하게 된다.
Averagepool 사용으로 피처맵 내의 모든 정보를 고려할 수 있게 되는 듯 하다.
Growth Rate
각각의 function H가 k개의 피처맵을 생성하면, n번째 레이어의 피처맵 개수는 k0 + k(n-1)개가 된다. (k0은 input 레이어의 채널 수)
기존 네트워크 구조들과 DenseNet의 중요한 차이는, DenseNet이 매우 좁은 레이어를 가졌다는 것이다.(k = 12, k는 네트워크의 growth rate며, hyperparameter다.)
각 레이어에서 k개의 피처맵을 뽑을지 결정하는 것 = 전체 output에 어느정도 기여할지 결정하는 것
DenseNet은 상대적으로 작은 growth rate로도 sota 모델을 달성하기 충분한 결과를 얻었다.
Bottleneck Layers
각 레이어가 k개의 output 피처맵을 생성하지만, 일반적으로 더 많은 input이 필요하긴 하다.
Bottleneck layer에서는 1x1 conv를 사용하여 input 레이어 피처맵의 수를 줄임으로 3x3 conv가 처리해야 할 데이터 양을 감소시킨다. (Computational efficiency 향상)
Compression
모델의 compactness를 향상시키기 위해, transition layer의 피처맵 수를 줄일 수 있다.
Dense block이 m개의 피처맵을 포함하면, transition layer는 θm개의 output 피첩맵을 생성하는데, θ가 compression factor다.
Implementation Details
ImageNet 데이터셋을 제외한 모든 데이터셋에서, DenseNet은 각각 동일한 개수의 레이어를 가진 3개의 Dense block으로 구성된다.
자세한 네트워크 정보는 아래 표를 참고하면 된다.
input은 224x224 이미지다.
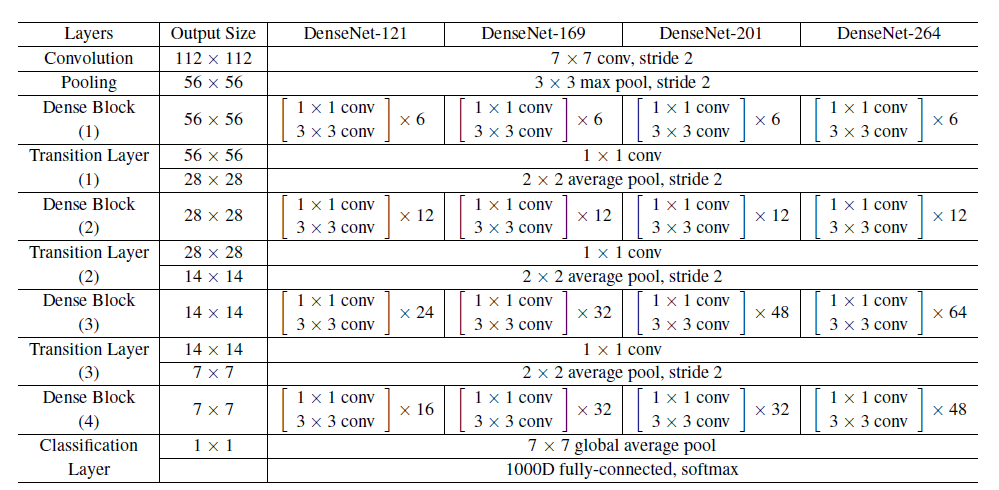
🍞4. Experiments
Dataset - CIFAR, SVHN, ImageNet
Optimizer: SGD
Batch size: 64(CIFAR, SVHN), 256(ImageNet)
Epoch: 300(CIFAR), 40(SVHN), 90(ImageNet)
Learning rate: 0.1, 점차 감소(자세한건 논문 참고)
Weight decay: 0.0001, momentum 0.9
Dropout prob: 0.2
Data augmentation: X
결론적으로 Parameter efficiency가 뛰어나고, residual network에서 발생하는 overfitting, optimization 문제를 줄였다.
특히 실험 설정이 ResNet에 최적화되어 있는 상태라, 더 높은 성능을 기대할 수도 있다.
🍞5. Discussion
ResNet과 짱 유사해보이지만, summation 대신 concatenation을 사용한 작은 차이가 정~말 큰 차이가 되어버린다.
Model compactness
input concatenation의 직접적인 결과로 피처맵은 모든 subsequent 레이어에 접근이 가능하다.
-> 피처 재사용 + 더 compact한 모델
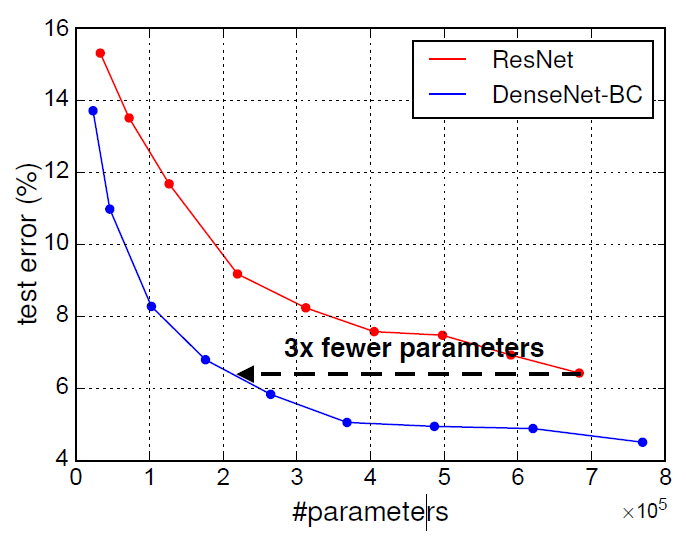
암튼 DenseNet이 ResNet에 비해 parameter 대비 성능 더 좋다.
Implicit Deep Supervision
왜 정확도가 향상되냐, 각 레이어들이 short connection을 통해 loss function의 추가적인 supervision을 받기 때문이다.
Stochastic vs. deterministic connection
Dense conv network와 Stochastic depth regularization of residual network 사이에, 흥미로운 하나의 connection이 있다.
Stochastic depth에서 residual network의 레이어들은 랜덤하게 drop되고 주변 레이어 사이에 direct connection이 생성된다.
Pooling 레이어는 drop되지 않기 때문에 네트워크는 DenseNet과 유사한 connectivity pattern을 갖는다.
-> 방법은 다르긴 한데 stochastic depth에 대한 DenseNet의 해석은 이러한 reglularizer의 성공에 대한 인사이트를 제공한다.
Feature Reuse
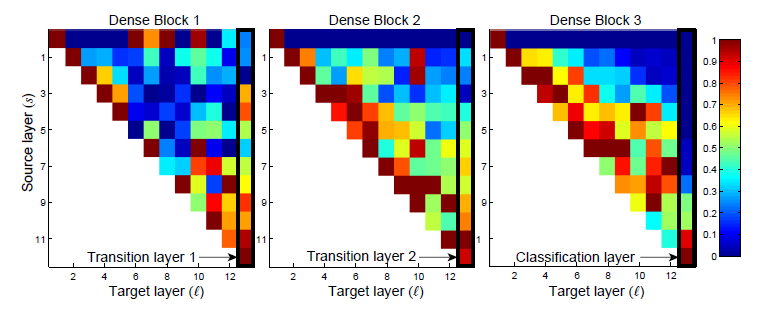
3개의 Dense block에 대한 히트맵인데,
초기 early 레이어에서 추출된 피처들이 dense block 내의 깊은 레이어에서 직접적으로 활용됨을 의미한다.
사실 더 자세하게 적고싶었는데... 논문 전체 리뷰다보니까 생각보다 힘들어서 여기까지만 적겠다. 더 자세한건 논문 참고!
🍞6. Conclusion
같은 피처맵 크기를 가진 any two layers에 대한 direct connection에 대해 소개했고,
DenseNet은 optimization difficulty 없이 레이어의 규모를 증가시킬 수 있음에 대해 증명했다.
DenseNet은 parameter의 개수가 증가할수록 오버피팅이나 성능 저하가 없이 정확도가 향상된다.
게다가, 다른 네트워크 구조들에 비해 적은 parameter 개수와 연산량으로 더 좋은 결과를 냈다.
