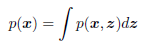
요새 여러 DDPM 논문들을 읽고 있는데, 서베이 논문(인지는 모르겠지만)으로 잘 정리하면 좋겠다 싶어 글을 써본다. 수식을 보면 읽기가 싫어져서... 글을 써야 이해하려고 노력이라도 할 것 같다.
🍞 Introduction: Generative Models
생성 모델의 주 목표는 뭘까?
바로 관심 있는 분포로부터 관찰된 샘플 x 의 실제 데이터 분포 p(x) 를 아는 것이다.
p(x)를 학습한 후에는, 근사한 분포의 새로운 샘플을 임의로 생성할 수 있다. 일부 formulation에서는 관찰되거나 샘플링된 데이터의 likelihood를 평가할 수도 있다.
생성 모델은 여러 종류가 있는데, 간단히 나열만 하겠다.
- GAN(Generative Adversarial Networks, 생성적 적대 신경망)
- Likelihood-based models(가능도 기반 모델): autoregressive models, normalizing flows, VAE(Variational Autoencoders)
- Energy-based modeling
- Score-based generative model: 에너지 기반 모델의 점수를 신경망으로 학습한다.
Diffusion model: likelihood-based + score-based
🍞 Background: ELBO, VAE, and Hierarchical VAE
우리가 관찰하는 데이터는 보이지 않는 잠재 변수(latent variable)에 의해 생성되거나 표현될 수 있다.
Plato's Allegory of the Cave: 동굴 안의 사람들은 자신들 앞의 벽에 투영된 2차원 그림자만을 볼 수 있다. 2차원 그림자는 그들이 볼 수 없는 3차원 객체에 의해 생성된다. 그들은 3차원 객체를 보거나 완전히 이해할 수는 없지만, 추론하고 추측할 수는 있다.
이러한 관점에서, real world에서 우리가 관찰하는 객체(얻는 데이터)들도 보이지 않는 더 높은 차원의 잠재 변수에 의해 생성된다고 볼 수 있다. 잠재 변수를 직접적으로 관찰할 수는 없지만 데이터를 통해 그것에 대해 학습, 추론할 수 있다.
하지만 생성 모델에서는 더 낮은 차원의 잠재 표현을 학습하려 한다.
더 높은 차원의 표현을 학습하려는 것은 강력한 사전 정보 없이는 무의미함.
더 낮은 차원 학습 = 압축(Compression) -> 의미있는 차원 표현 학습
👀 Evidence Lower Bound (ELBO)
관측 데이터 x, 잠재 변수 z에 대해 공통 분포 p(x,z)가 존재한다.
관측값 x에 대해 likelihood가 최대가 되는 p(x)를 찾는 것이 likelihood-based 방식이다.
p(x)와 z에 대한 p(x,z)가 일치하게 되면 관측값들과 일치하는 데이터를 생성할 수 있기 때문이다.
-> 아래의 수식대로 모델을 학습시킨다.

확률에 대한 chain rule에 의해 p(x)를 아래와 같이 나타낼 수도 있다.

ELBO의 식은 다음과 같다.

Evidence는 p(x)를 의미하는데, p(x)에 대한 하한(lower-bound)를 z에 대한 식으로 만든 것이다.
ELBO의 최대화 = p(x)의 하한 최대화 = p(x) 최대화

좀 더 자세히 뜯어보면,

기댓값, 옌센부등식, KL divergence는 검색하면 나오니까... 설명 생략
👀 Variational Autoencoders (VAE)
VAE는 ELBO를 최대화하는 것으로 학습된다.
AE는 입력 데이터가 중간의 bottlenecking 단계를 거친 후 자기 자신을 예측하도록 훈련됨.
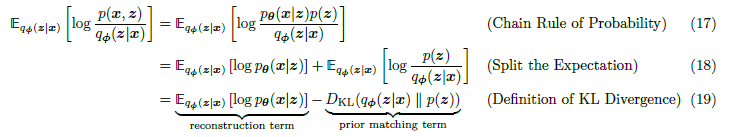
(18)의 좌측 부분은 Decoder에서 p_theta(x|z)를 학습하고, (19의 우측 부분은 Encoder에서 bottleneck distribution인 q_pi(z|x)를 학습한다.
KL Divergence를 최소화하고 (17)의 좌항을 최대화하면 ELBO를 최대화할 수 있다.
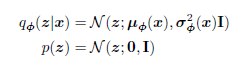
VAE의 Encoder는 diagonal covariance를 갖는 다변량 가우시안을 모델링한다.
입력 데이터 x로부터 잠재 변수 z의 분포를 표현하기 위해 사용되는데, prior(사전 분포)는 표준 다변량 가우시안 분포로 선택되는 경우가 많다.
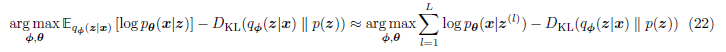
ELBO의 수식을 Monte Carlo Approximation을 사용하여 근사한건데, 이를 통해 VAE는 입력 데이터를 잘 reconstruction할 수 있고, 잠재 공간을 통해 데이터의 복잡한 분포 또한 효과적으로 학습할 수 있다.
👀 Hierarchical Variational Autoencoders (HVAE)
VAE보다 더 high-levl의 잠재 변수를 이끌어내기 위해 VAE를 hierarchical하게 쌓은 모델이다.
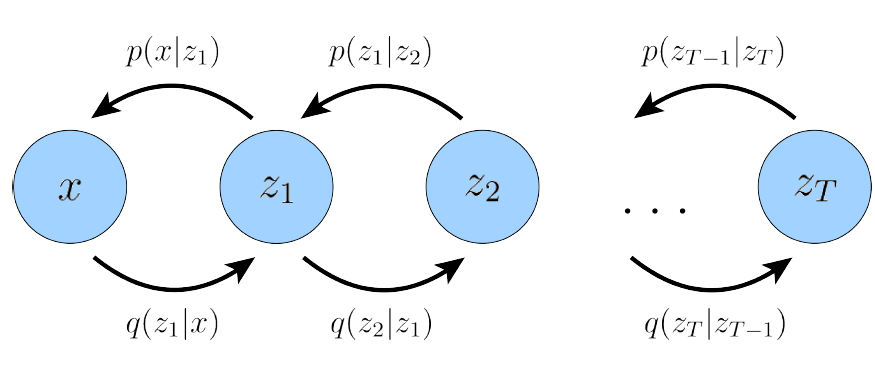
Markov Chain에 대한 수식은 아래와 같다.
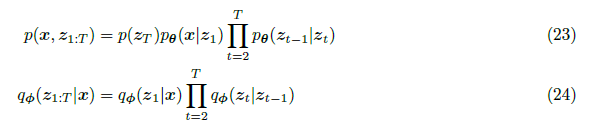
이제 ELBO를 도출하면,

(23), (24)를 (28)에 대입하면 최종적으로,
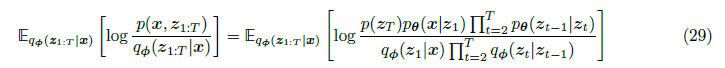
이게 Variational Diffusion Models의 기본이 되는 수식으로, 짱 중요!!!!!!!!!!!!!!!!!
