본 글은 Stanford CS224N Winter 2021의 강의를 듣고 정리하는 내용입니다.
Youtube : Stanford CS224N
Website : Stanford CS224n : Natural Language Processing with Deep Learning
1. Human language and word meaning
- Human language는 빠른 것이 중요한 네트워크와는 달리 느림
- 하지만 효율적이기 때문에 지금껏 사용됨
- 현대의 기술보다는 느리지만, 생성되는 결과물의 다양성과 구체성이 높음
- 무작위로 단어를 배열해놓아도 뜻을 유출할 수 있음
- 나는, 상상하다, 축구선수, 미래 → 뜻의 유추가 가능
⇒ 각 단어들의 의미를 파악해서 의사소통을 진행할 수 있음.
이 때 ‘의미’를 파악하는 방법은?
1) Denotational semantics : 표시 의미론
- 심볼을 통해 의미를 파악함
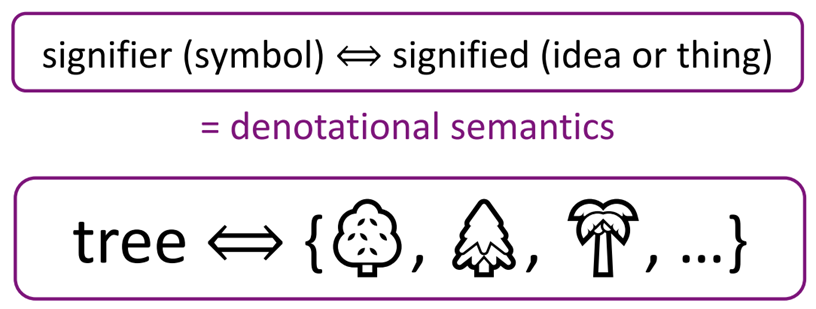
- a를 가리키는 심볼을 정해두고, 그 심볼을 보면 a를 떠올리는 것
⇒ 과거에는 컴퓨터에서 단어의 뜻을 파악하기 위해, 표시의미론을 사용하는 WordNet을 사용함
- a를 가리키는 심볼을 정해두고, 그 심볼을 보면 a를 떠올리는 것
📌 WordNet

- 각 단어들에 대해 동의어 및 상하관계(”is-a” relationships)의 언어를 저장해놓은 리스트 (컴퓨터용 언어 백과사전이라고 이해하면 될 듯함)
- WordNet의 문제점
- 뉘앙스를 구분하기 어려움 : 각 문맥에 따라서 뜻이 달라지는 경우가 있지만 파악하기 어려움
- 신조어 관리가 어려움 : 신조어 등이 발생하면 지속해서 업데이트를 해주어야 함. 인력 자원 소모.
- 각 단어에 대한 뜻이 주관적으로 저장될 수 있음
- 유사도 관계를 계산하기 어려움 ⇒ 이 문제를 해결하기 위해 전통적 NLP에서는 각 단어를 discrete symbol 로 나타내고자 함
One-hot vector : Representing words as discrete symbols
-
One-hot : 하나의 1, 나머지는 0
-
단어의 의미 해당하는 곳을 1로, 나머지는 0으로 표시하는 지역주의적 표현
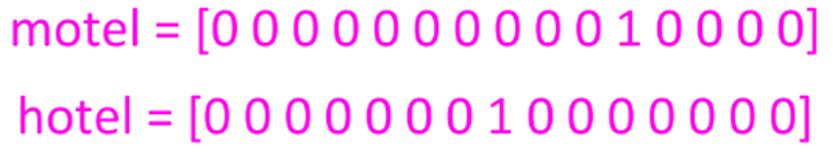
-
벡터의 차원 = vocabulary에 속하는 단어의 개수
-
만약 vocabulary에 속하는 단어가 500,000 개라면 벡터도 500,000 차원이어야 함
⇒ 무한 개의 단어에는 무한한 벡터가 필요하므로 사실상 불가능
-
-
단순히 단어의 뜻에 1만 표기하고 있기 때문에, 단어 간의 유사도에 대한 정보가 없음
- One-hot vector에는 유사도에 대한 개념이 없음
⇒ 벡터 자체에 유사도를 학습시켜야겠다!
2) Distributional semantics : 분산 의미론
“You shall know a word by the company it keeps” - J.R Firth 1957:11
- 단어의 의미는 그 주변에 주로 나타나는 다른 단어에 의해 파악할 수 있음 (-어느 사람을 알고 싶다면 그 사람의 주변인들을 봐라-와 비슷한 맥락)
- w라는 단어가 있을 때, 그 주변에 있는(앞뒤로 fixed-size window에 속한) 단어를 보면 context를 알 수 있음
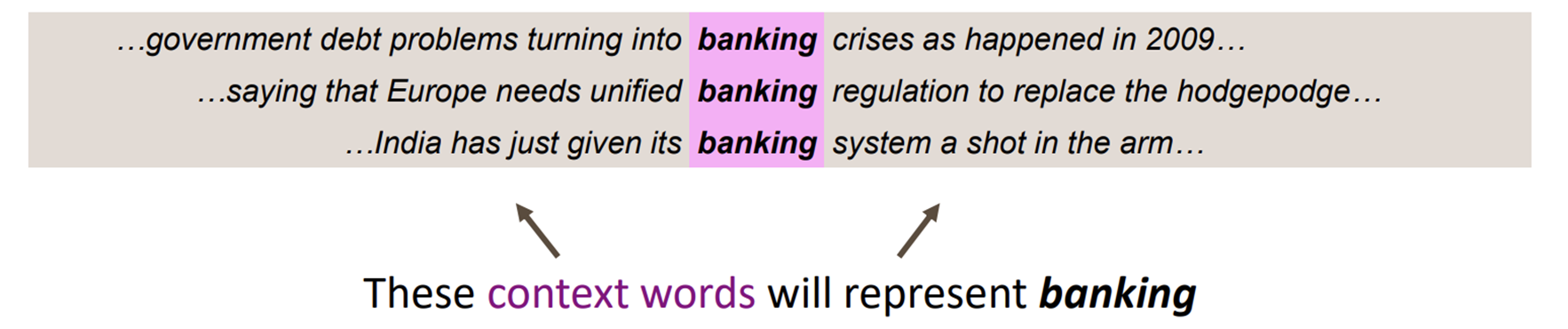
Word vectors (=Word embeddings / Word representation)
- One-hot vector처럼 대부분이 0인 무의미한 벡터가 아닌, 모두가 유의미한 값을 가지고 있는 dense vector를 각 단어에 대해 생성함
- 유사한 context에서 나타나는 단어들은 서로 그 벡터가 유사하게 생성될 것임!
- 두 벡터 간의 dot product(내적)를 통해 유사도를 측정할 수 있음

❓ Word embedding이라고 불리는 이유
-
Word vector들을 표현한 Vector space를 확인하면 비슷한 단어들끼리는 가까이에 함께하고 있음.
-
이 때 Word vector는 고차원이므로 하나의 vector를 확인하려면 여러 번 파고 들어가야 함 = vector가 파묻혀있음 = Word Embedding

2. Word2vec introduction
Word vector를 학습하기 위한 프레임워크
Idea
-
Corpus (body of text) : 여러 단어들로 이루어진 말뭉치 - 가 있을 때
-
Corpus(=Fixed vocabulary) 내에 포함된 모든 단어는 vector로 표현됨 (초기에는 random vector를 부여함)
-
Corpus 내의 특정 포지션 t에 대하여, center word c와 context(=outside) words o를 파악함
- Window size m에 따라서 o에는 t-m번째 ~ t+m번째 단어가 포함됨 (t번째는 center word c니까 제외)
-
c가 주어졌을 때 o가 나타날 확률을 계산하기 위해 c와 o의 벡터 간 유사도를 사용함
-
그 확률(c가 주어졌을 때 o가 나타날 확률)을 최대화하기 위해 계속해서 word vector를 조정함
❓ 왜 c가 주어졌을 때 o가 나타날 확률을 높이기 위해 노력하는가?
-
현재 corpus는 실제로 사용되는 문장들임
-
따라서 c가 주어졌을 때 그 주변에 있는 o는 그렇게 사용되는 게 맞는 것! (o들이 나올 때는 c가 나와야 한다는 정답이 주어진 것!)
-
따라서 c 주변에 o가 있을 확률은 높아야 함 (실제로 그렇게 사용되고 있다는 거니까!)

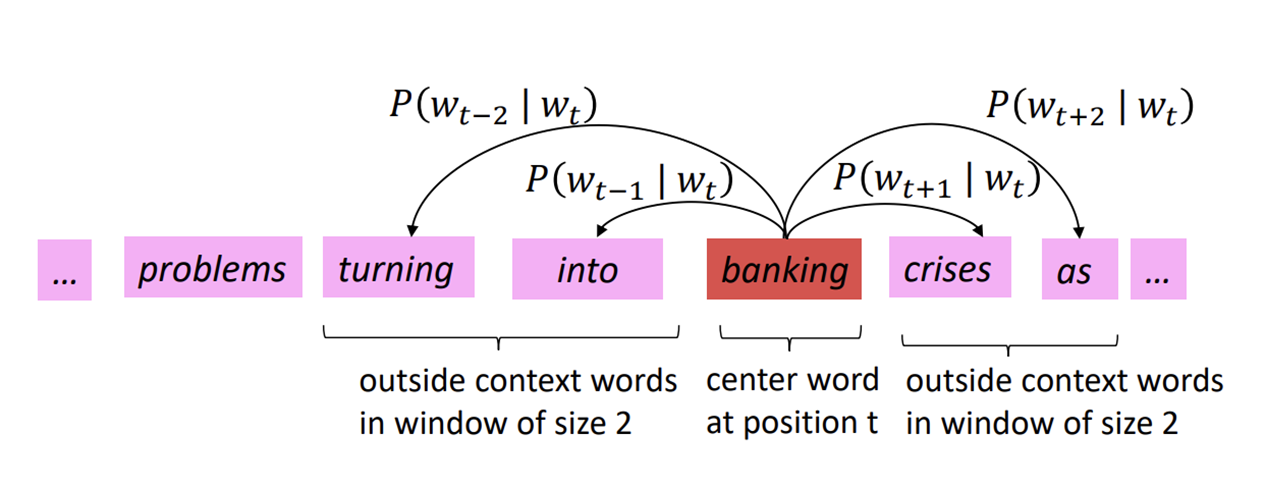
-
Word2vec : objective function (=loss function, 손실함수)
Likelihood :
Likelihood (가능도, 우도)
- 어떤 값이 관측되었을 때, 이것이 어떤 확률 분포에서 왔을 지에 대한 확률
- θ(center word)가 관측되었을 때 현재의 Context word가 해당 위치에 있을 확률
⇒ 확률이 높은 게 좋은거니까 Likelihood는 최대화되어야 함!
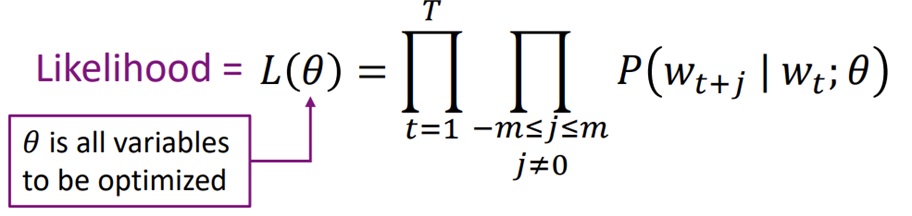
Objective function (Loss function) :
목적함수 (=손실함수)
- Average negative log likelihood
- Likelihood에서
- 값을 최소화하기 위한 negative
- 곱을 합으로 나타내기 위한 log
- 평균을 위한
⇒ 손실이 가장 적어야 좋은 거니까 Objective function의 값은 최소화되어야 함!
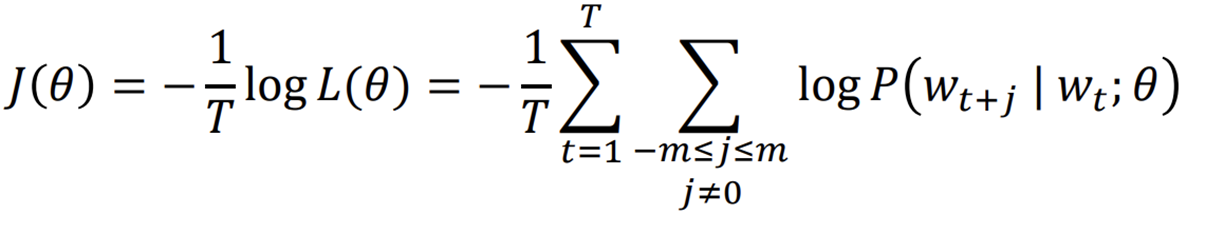
∴ Minimizing objective function ⇔ Maximizing predictive accuracy
⇒ 앞으로는 Objective function을 최소화함으로써 Word2vec의 성능을 높일 것임!
How to calculate
- 각 단어는 두 개의 word vector를 가지고 있음
- : w가 center word일 때의 word vector
- : w가 context word일 때의 word vector
∴ center word c와 context word o에 대해서

🤯 왜 이런 식이 나오는가?
- 와 의 dot product : o와 c의 유사도 비교(값이 클수록 유사함)
- 확률(P)은 모두 양수여야 하는데, u와 v의 내적은 음수일 수도 있으니 exponentiation을 통해 negative probability를 피함
- 확률은 0과 1 사이의 값이어야 하므로 c가 주어졌을 때 vocabulary 내의 모든 단어의 확률의 합을 통해 정규화
⇒ 이건 softmax function의 일종임
Softmax function
- 입력받은 값을 출력으로 0~1 사이의 값으로 모두 정규화하며, 출력값들의 총합은 항상 1이 되는 특성을 가진 함수
⇒ “max” : 큰 값은 1에 가깝게 만들어 줌
⇒ “soft” : 작은 값은 0에 가깝게 만들어 줌
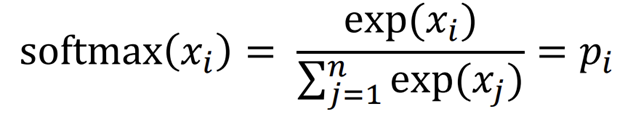
To train model : Optimize value of parameters
- loss를 최소화하기 위해 parameter를 조정해야 함
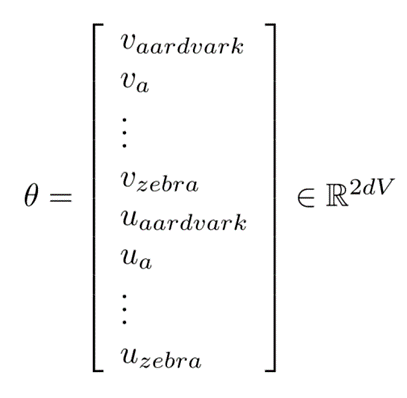
- 목적함수의 유일한 매개변수 θ
- 모든 model parameters를 one long vector로 나타낸 것
- 현재 corpus(vocabulary)에 V개의 단어가 있고, 각 word vector가 d-dimensional vector일 때
- 각 단어는 vector를 두 개씩 가지고 있으므로 2dv
- 우리는 이 파라미터를 기울기 경사를 감소시키면서 최적화해야 함
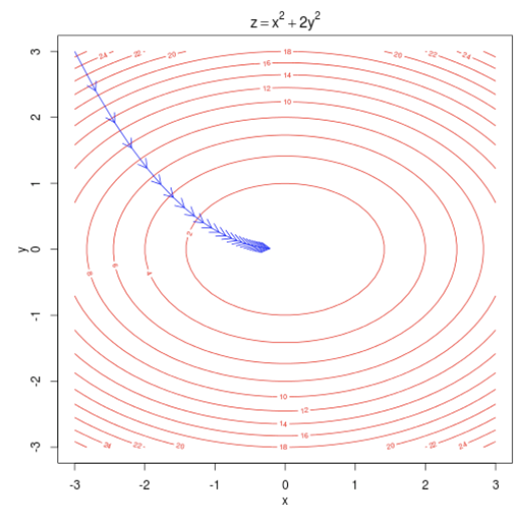
3. Word2vec objective function gradients
따라서 목적함수의 기울기를 구하는 법을 알아보고자 한다.
📏 사용되는 수학 개념
: 편미분 기호 - 미분을 통해 기울기를 구할 수 있음
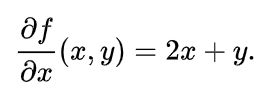
이러한 함수 f가 있다고 할 때, x에 대한 편미분을 구하면 ⇒ x가 아닌 y는 상수로 취급하여 계산하고 x의 제곱은 2x가 됨
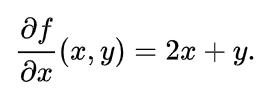
출처 : 편미분이란?
log * exp
- log * exp는 상쇄됨
- log(k)는 e를 몇제곱해야 k가 나오는지를 구하는 것
- exp(x)는 e의 x제곱
∴ log(exp(x)) = x
Chain Rule
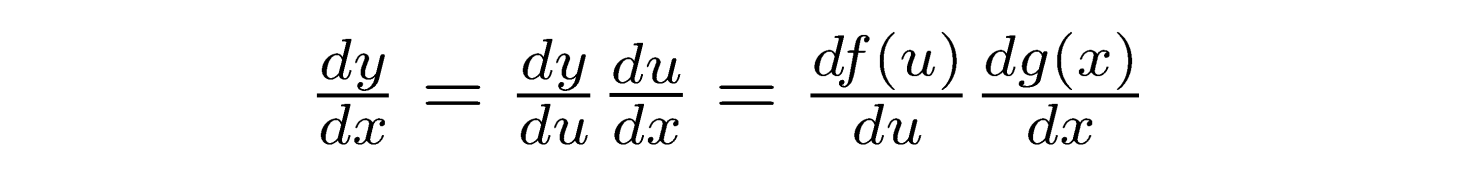
자연로그의 미분
미분
 |
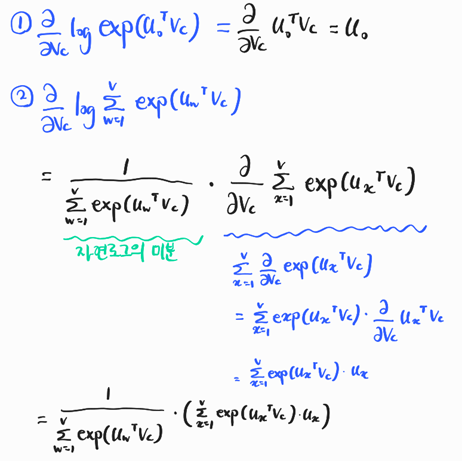 |
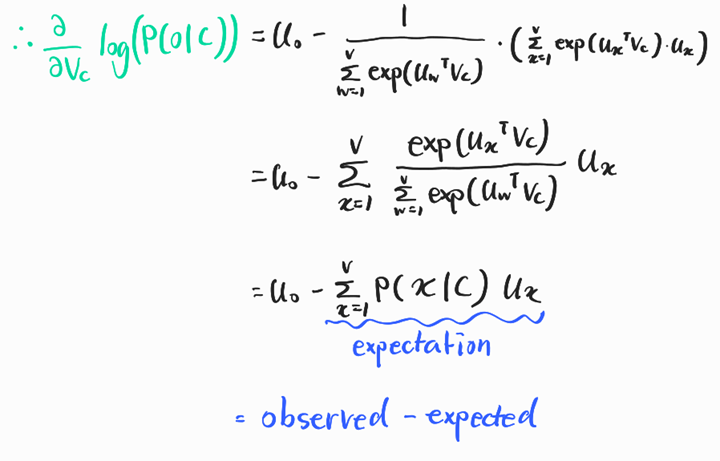
⇒ 기울기가 0에 가까워야 하니까, 실제 context word와 예측된 context word 간의 차이가 적을수록 모델의 성능 ↑
영상 강의는 여기에서 끝났는데, 강의자료는 아직 남아있어 조금 혼란이 있었다. 하지만 해당 자료는 다음 강의에 나오는 것을 확인하였다.
딥러닝이나 머신러닝에 대해서는 아는 바가 아예 없어서 강의를 이해하는 데 조금 힘들었는데, 특히 수학을 건들지 않은 지가 오래 되어서..^^ 공식 이해에도 어려움이 있었다. 앞으로도 천천히 이해해야할 것 같다.
