[논문리뷰] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (2020) 논문 리뷰
Introduction to NeRF

우리가 게임 등에서 어떤 3D 객체를 360도로 돌려보면서 다양하게 바라보기 위해서는 3D 랜더링이 필요하다. 일반적으로 3D 랜더링을 할 때 mesh, point cloud, voxel 등의 3D representation이 사용되며, SfM(Structure from Motion)과 같은 알고리즘을 활용해 객체를 여러 방향에서 찍은 2D 이미지로부터 3D shape을 복원할 수 있다.
(참고: https://velog.io/@gjaegal/3D-vision-shape-representation)
반면, 본 논문에서는 2D 이미지로부터 3D shape을 '직접' 복원하는 것이 아니라 객체를 바라본 모든 방향에서의 view(2D 이미지)를 생성하는 view synthesis task를 다룬다. 마치 물체를 3D 랜더링한 것처럼 모든 방향에서 바라볼 수 있게 된다는 것이다.
먼저 Volume Rendering이란?
Volume Rendering
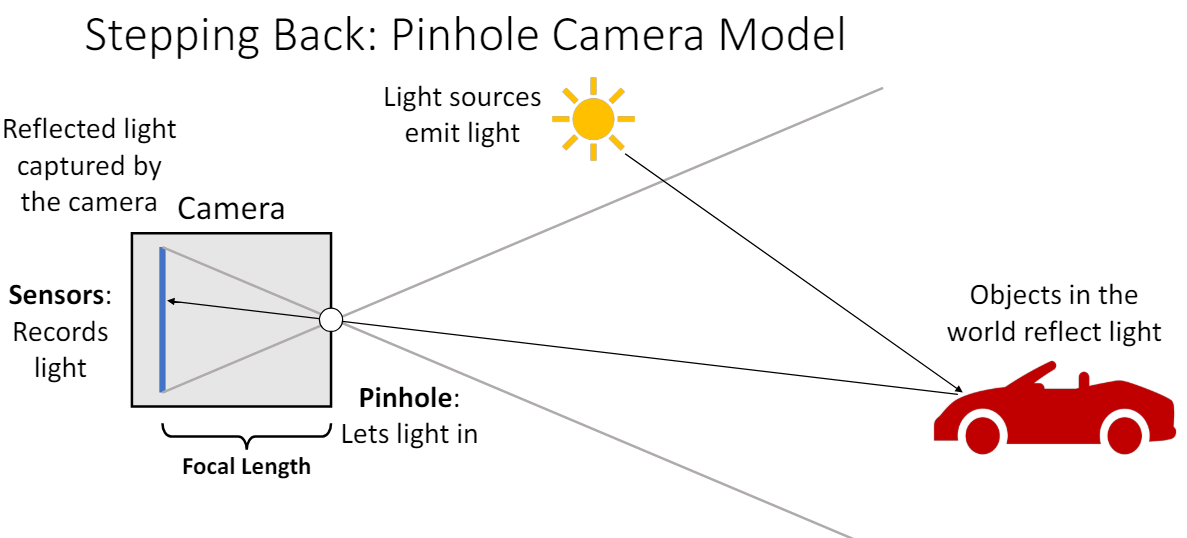
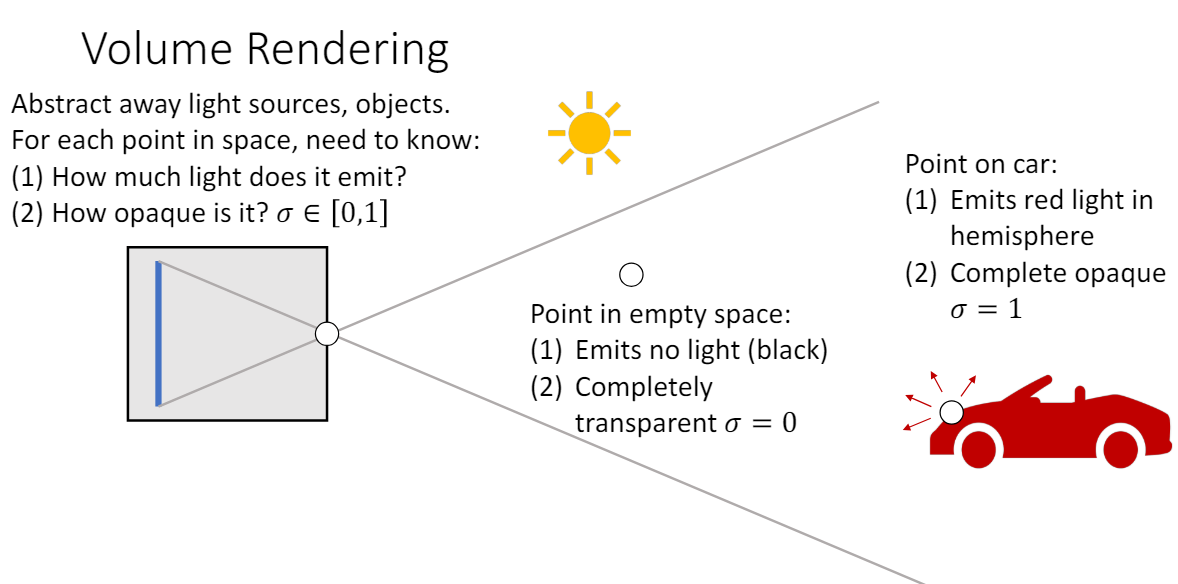
Volume Rendering은 컴퓨터 그래픽스에서 3D 공간을 2D에 투시하여 나타내는 방법이다. 3D 세상을 카메라로 사진을 찍을 때의 원리를 생각하면 된다. 광원에서 나온 빛은 빨간색 차의 표면에서 반사되어 카메라 렌즈로 들어가서 상이 맺히게 되고 우리가 2D 이미지로 볼 수 있게 된다.
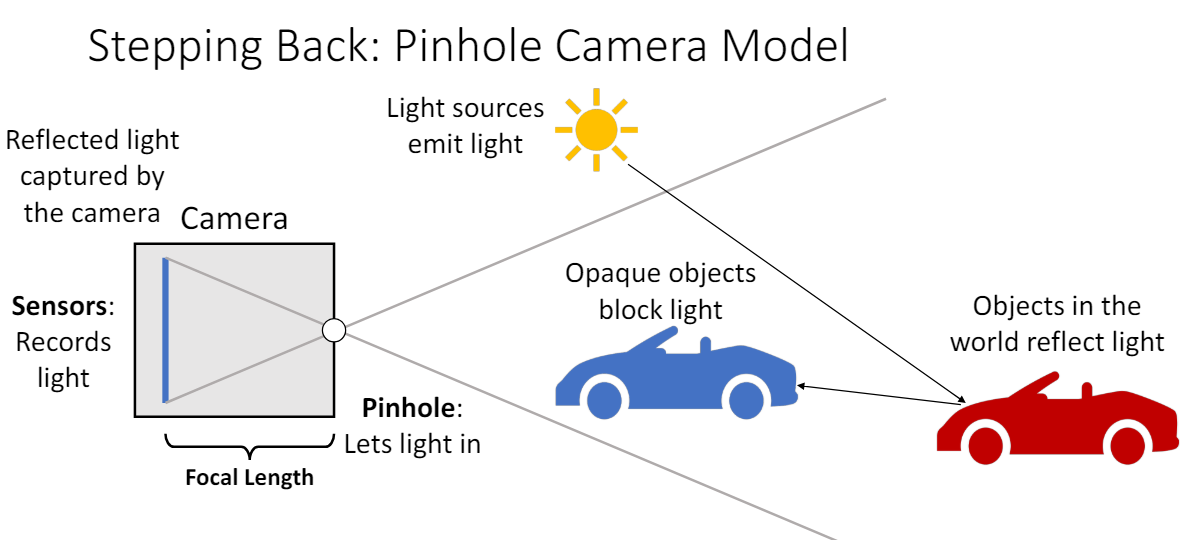
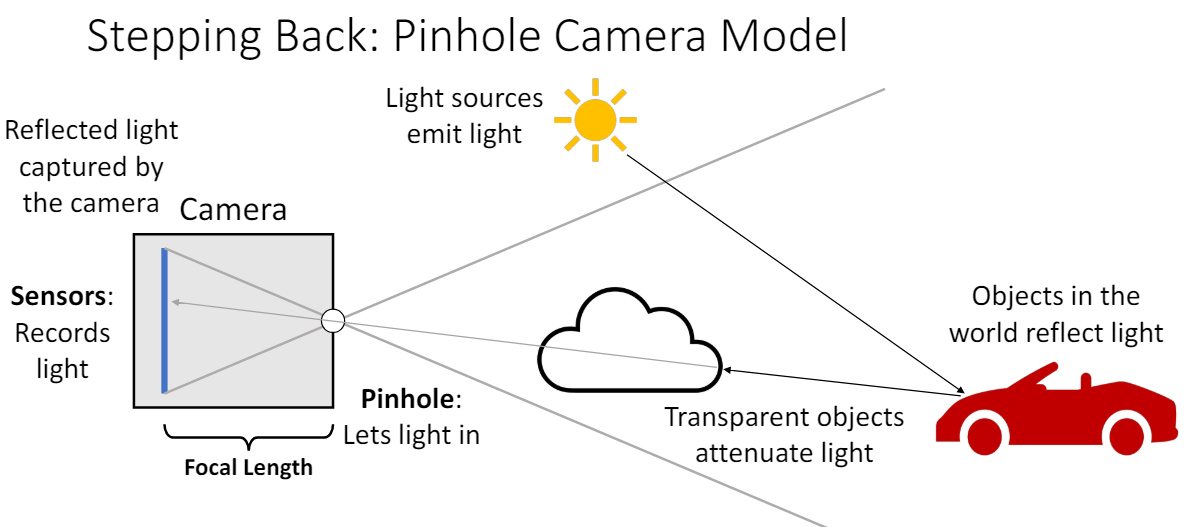
이때 카메라 위치와 물체(빨간색 차) 사이에 다른 파란색 차가 있으면 가려서 해당 빛을 막을 것이고, 투명한 유리가 있으면 그대로 빛이 통과하여 도달하게 된다. 빛이 파란색 차를 통과하지 못하는 이유는 파란색 차의 volume density 값이 1에 가깝기 때문이고, 반대로 공기나 투명한 유리는 volume density 값이 0에 가깝다.
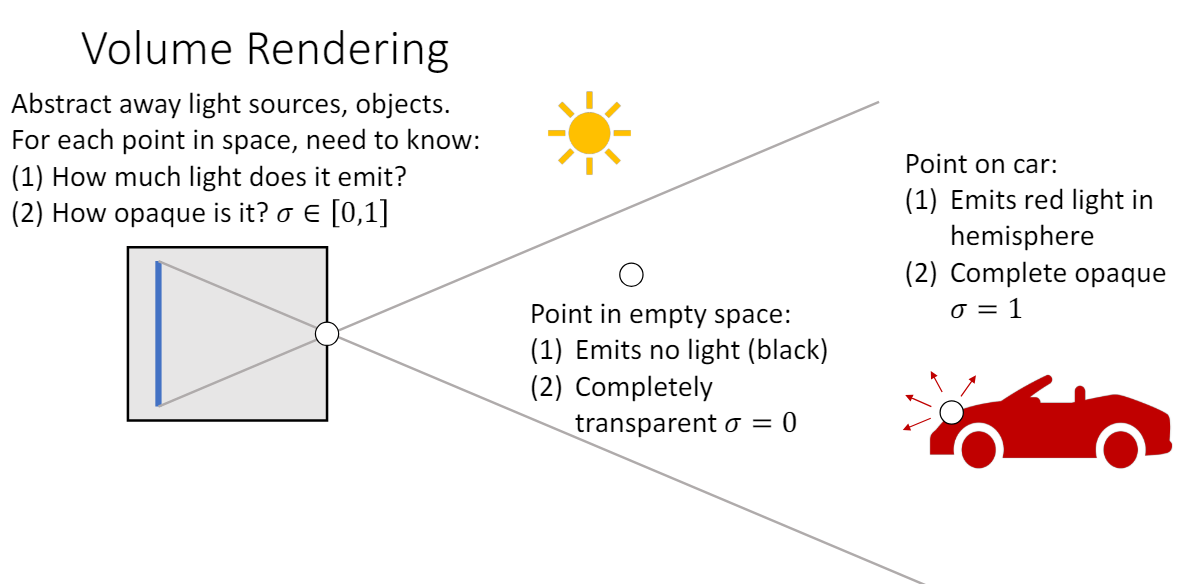
공간의 각 점에서의 색깔과 불투명도를 모두 알면 volume rendering을 통해 카메라에 맺히는 2D 이미지를 계산할 수 있다. 즉, 카메라(ray origin)에서 봤을 때의 이미지를 얻으려면 공간의 각 점에서 내보내는 RGB 값과 volume density 값을 알아내기만 하면 된다. 그렇다면 volume rendering은 구체적으로 어떻게 이루어지는 걸까?
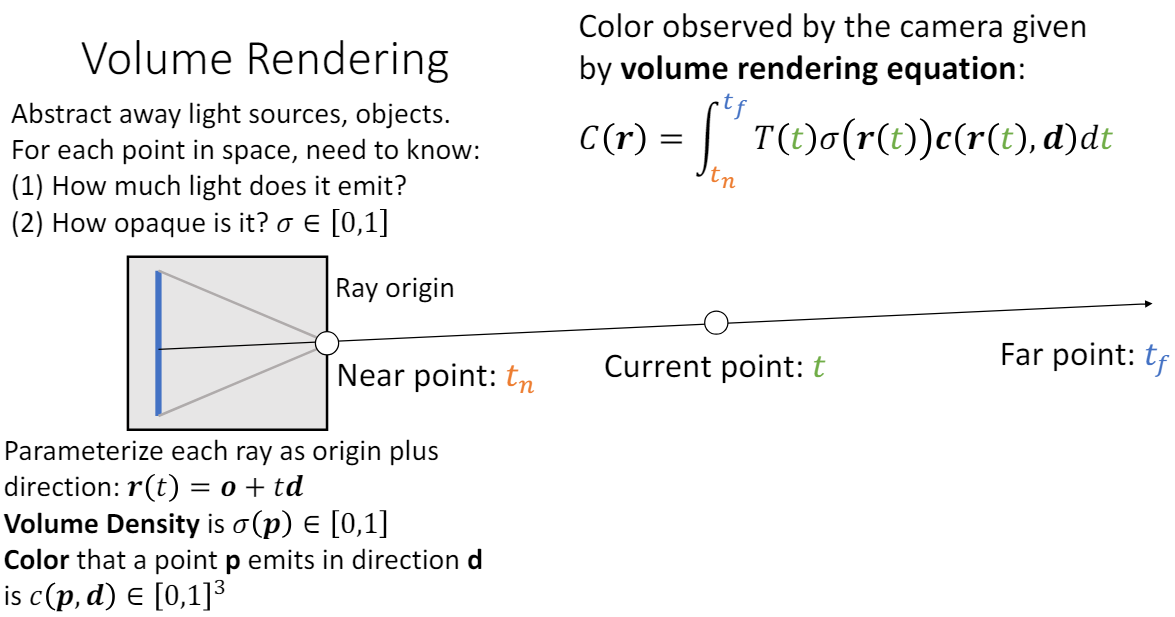

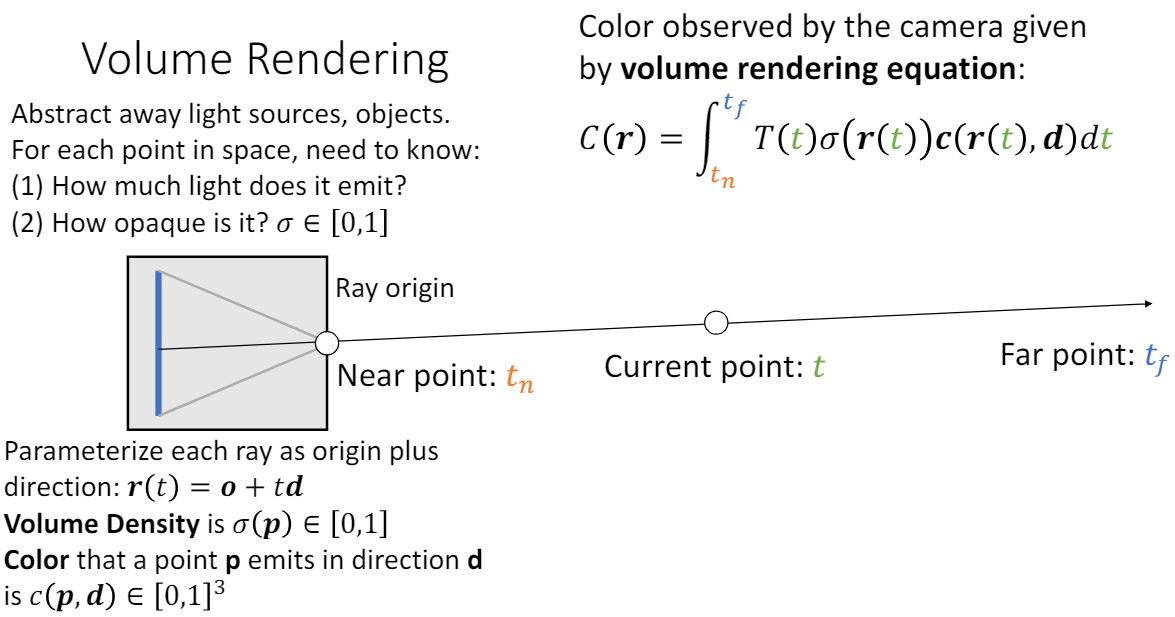
ray 방향에서 "관찰되는" 색 C(r)은 volume rendering equation으로 계산할 수 있다.
: 시점 t에서 ray 상의 위치 (점)
: transmittance, 점 r(t)에서 반사된 빛은 카메라에 얼마나 도달할 것인가?
~까지 ray 위에서 opacity 적분값
: opacity, 점 p에서의 volume density
: color, 점 p에서 d방향으로 "내보내는" 색
이렇게 모든 ray에 대해 C(r)을 계산하면 해당 장면을 카메라에서 찍은 2D image를 만들 수 있다.
NeRF 논문 리뷰
Abstract
-
Synthesize novel views of a sceneby optimizing a continuous volumetric scene function w/ a sparse set of input views -
how to effectively optimize complicated scenes
1. Introduction
- scene representation
딥러닝은 함수를 학습하는 것이다. MLP로 scene function을 학습하여 scene을 표현해보자.
scene function:
view-dependent color : 공간상의 각 point P()에서 특정 direction d()으로 내보내는 색을 output
Volume density : 각 point()에서 density(불투명도)를 output
- 정리하자면, 특정 view(direction d)에서 본 2D 이미지를 rendering하기 위해 거치는 과정은 다음과 같다.
1) image에서 각 pixel에 해당하는 각 camera ray에서 여러 개의 3d point를 샘플링한다. (위치 x)
2) x와 d를 MLP에 넣어서 를 얻는다.
3) volume rendering을 사용해서 해당 시점에서의 2D 이미지로 바꾼다.
- 다양한 view에서 rendering된 이미지와 true image 사이의 error을 최소화하도록 optimize한다.
함수를 잘 학습할수록 어떤 위치에서 실제 scene에 맞는 color와 density를 output하게 된다.
이 과정이 잘 작동하려면 optimization이 잘 되는 것이 중요하다.
하지만 기본적인 방법으로 optimize할 경우 충분히 high resolution으로 converge하지 않으며, 필요한 sample의 수도 inefficient하다. 이를 해결하기 위해 저자들은 추가적으로 다음의 2가지 방법을 사용했다.
1) positional encoding
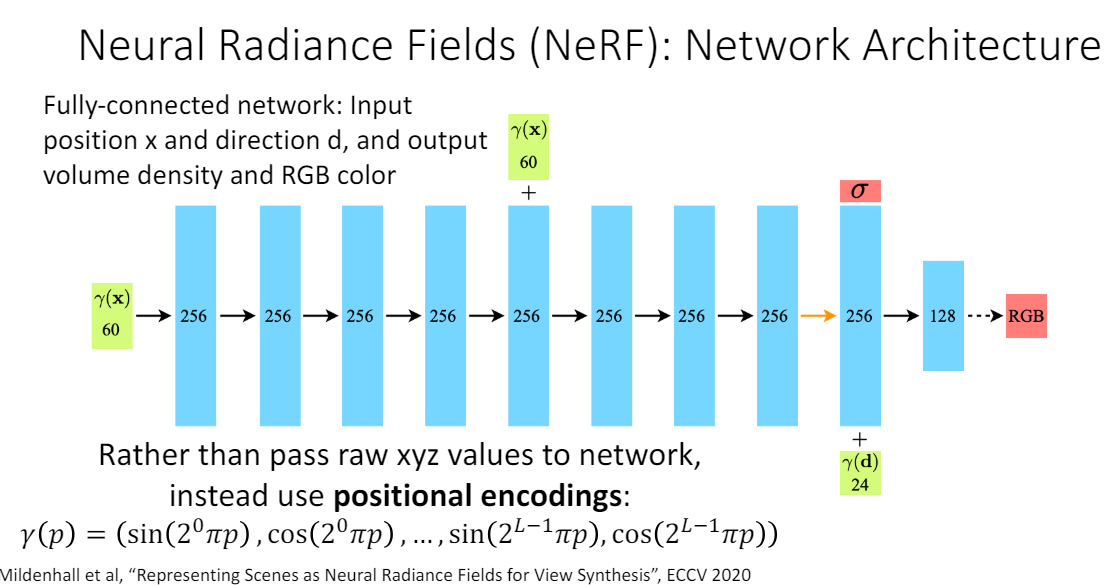
input 5D 좌표(위치 x= + 방향 d=)를 먼저 더 높은 차원으로 변환한 뒤에 network input으로 넣는다. 이렇게 하면 우리가 필요한 high frequency variation(color, geometry)도 잘 나타낼 수 있게 된다.
encoding function :
이 function은 x의 각 요소 (x,y,z)와 d의 각 요소에 대해 적용되는데, 이러한 mapping은 transformer의 positional encoding 과정과 유사하지만 용도가 다르다. transformer에서는 순서를 고려하기 위한 위치 vector를 만들 때 사용되었고 NeRF에서는 단순히 higher dimension space로 올려주기 위한 방법이다.
2) hierarchial sampling procedure
각 camera ray 당 N개의 "일정한" 간격의 query points에서 sampling하는 것은 비효율적이다. 왜냐하면 빈 공간과 앞 물체에 occlude된 공간은 해당 view rendering할 때 전혀 기여하지 않기 때문이다.
그래서 sampling을 두 단계로 나누어서 진행한다. 이를 위해 network를 두 개 만든다. 이를 각각 "coarse"와 "fine"이라고 부른다.
1) Stratified sampling으로 개의 sample 1 을 얻는다.
2) sample 1을 "coarse"에 넣어서 나온 color 을 color 의 weighted sum으로 본다. 에 기여하는 바가 큰 들의 weight가 클 것이다.
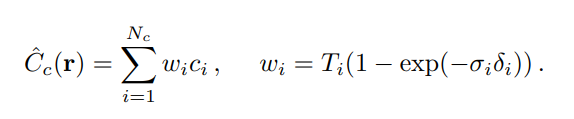
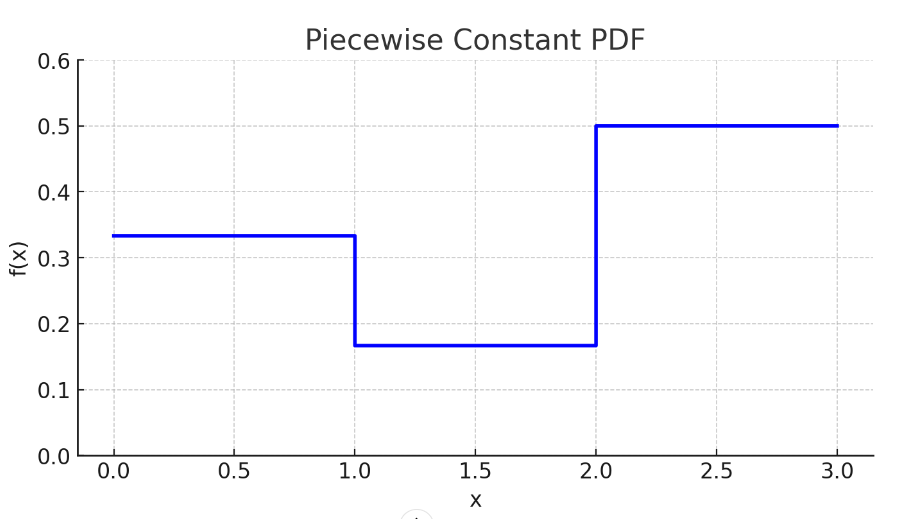
3) 이 weight들을 normalize하면 piecewise-constant PDF으로 볼 수 있다.
inverse transform sampling으로 이 PDF를 따르는 개의 sample 2를 얻는다. 기여하는 바가 큰 위치 근처에 sample들이 많이 생길 가능성이 높다. 다음 PDF 예시를 생각해보면 된다.
4) 와 sample이 겹치는 점에서 "Fine" network evaluation을 진행한다.
5) sample 위치에서 "fine"을 통해 color 을 얻는다.
이 과정으로 도출된 sample들은 visible content이 존재할 만한 위치에 더 많이 치우치게 된다. 효율적으로 sampling을 하게 된 것이다.
3. NeRF Scene Representation

density 는 위치 x만 따르면서 color 는 view dependent하게 하는 이유는 같은 위치가 view에 따라 다른 radiance를 가질 수 있기 때문이다. 이를 non-Lambertian effect라고 한다. input이 다른 점을 고려하여 MLP network를 다음과 같이 구성하였다.
x -> 8 FC layers -> & 256 feature vector
feature vector + d -> 1 FC layer -> RGB color
4. Volume Rendering with Radiance Fields
Recap)

실제로는 C(r)을 경로상의 모든 점들에 대한 continuous integral로 계산하지 않고, quadrature(구적법)으로 discrete한 점들에서 estimate한다.
Stratified sampling
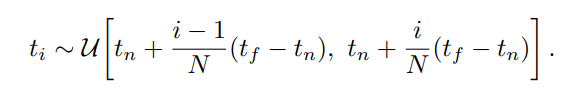
을 N개의 일정한 간격의 bin으로 나누고 각 bin에서 random하게 sample 을 추출한다. (총 N개) deterministic quadrature에서 일정한 간격의 정해진 점들을 사용하는 것과 달리, random한 위치를 사용할 수 있다. 결과적으로 MLP가 다양한 위치에서 evaluation될 수 있어서 continuous한 scene을 나타낼 수 있게 되는 것이다.
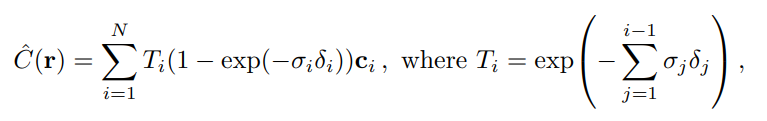
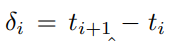
: 에서의 density, color set 을 estimate
same as alpha compositing w/
Implementation Details
optimization시, 사진의 모든 pixel로부터 camera ray batch를 얻고 각각 Nc+Nf개의 sample을 얻는다. 이때 loss는 다음과 같이 coarse와 fine을 모두 optimze한다. 그래야 fine network에서 sampling을 잘 할 수 있기 때문이다.
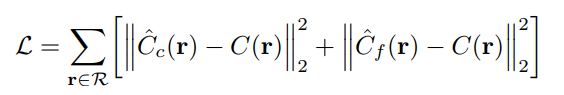
- batch size: 4096 rays
single scene takes 100~300k iterations on V100, 1~2 days
7. Conclusion
implicit function을 사용했을 때 input은 3D 대신 5D으로 개선했다. discrete voxel보다 좋은 결과를 보인다.
- Limitations
Interpretation 면에서 부족하다. redering quality가 기대만큼 좋지 않거나 failure mode을 분석할 때 neural network는 원인을 알기 어렵다.
Reference
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis (2020)
EECS 498-007 / 598-005: Deep Learning for Computer Vision
