NeRF 의 기본 개념은 간단한 편이지만, 막상 Dataloader 부터 from scratch 로 구현하려고 하면 어려운 부분이 많다.
그중에서도 ray casting 에 필요한 ray direction 과 ray origin 을 어떻게 구하는지 수식과 대응하는 line-by-line code 와 함께 알아보자.

1. Emission-Absorption Ray Casting

NeRF 는 장면을 렌더링하기 위해서 ray casting 을 이용한 volume rendering 을 구사한다. (NeRF Review)

NeRF 의 학습은 이를 통해 rendering 된 pixel 의 color 와, ground-truth color 간의 MSE loss 를 통해 이루어지기 때문에,

우리는 training image 의 모든 pixel 에 대해 적절한 ray $\mathbf{r}(t)$ 를 정의하여야 하며, 어떤 ray $\mathbf{r}(t)$ 는 다음과 같이 direction $\mathbf{d} \in \mathbb{R}^{3\times1}$ 와 origin $\mathbf{o} \in \mathbb{R}^{3\times1}$ 를 통해 정의할 수 있을 것이다.

이제 우리의 목표는 NeRF datasets 에서 제시된 정보들을 통해서 pixel-wise 로 적절한 $\mathbf{d}, \mathbf{o}$ 를 정의하는 것이다.

2. Camera to World Transformation

2.1. Preliminary

그렇다면 어떻게 2차원 이미지의 pixel 을 3차원 공간 상의 $\mathbf{d}, \mathbf{o}$ 정보로 바꿀 수 있을까?

이를 위해서 필요한 것이 camera-to-world transform , NeRF datasets 상에서 'transform.json' 으로 제공되는 데이터이다. 이 'transform.json' 을 열어보면 다음과 같은 정보들로 이루어진 json 파일임을 알 수 있는데,

"camera_angle_x": 0.6911112070083618,
"frames": [
    {
        "file_path": "./train/r_0",
        "rotation": 0.012566370614359171,
        "transform_matrix": [
            [
                -0.9938939213752747,
                -0.10829982906579971,
                0.021122142672538757,
                0.08514608442783356
            ],
            [
                0.11034037917852402,
                -0.9755136370658875,
                0.19025827944278717,
                0.7669557332992554
            ],
            [
                0.0,
                0.19142703711986542,
                0.9815067052841187,
                3.956580400466919
            ],
            [
                0.0,
                0.0,
                0.0,
                1.0
            ]
        ]
    },

여기서 우리가 사용하게 될 정보는,

1. 'camera_angle_x': 화각을 나타내는 intrinsic parameter. Focal length 를 구하는데 쓰인다.

2. 'transform_matrix': camera 좌표계로부터 공간 좌표계로의 변환 정보를 나타내는 extrinsic parameter. 통상적으로 rotation matrix $\mathbf{R} \in \text{SO}(3)$, translation vector $\mathbf{t} \in \mathbb{R}^{3 \times 1}$ 을 이용해 $\left[\mathbf{R} | \mathbf{t} \right] \in \text{SE}(3)$ 인 $4\times4$ matrix 로 나타내진다. (여기서 마지막 vector $[0, 0, 0, 1]$ 은 4D homogeneous coordinate 상의 계산을 위한 dummy 값이다)

   • 여기서 $\text{SE}(3), \text{SO}(3)$ 은 Lie Group 으로, lie group 과 lie algebra 간의 1:1 대응을 통해서 9개의 element 를 가진 rotation matrix 를 Degree of freedom (DoF) 3 만으로 나타낼 수 있다 (참조: rodrigues rotation formula).

3. cam2world transform 는, 공간 상의 절대적인 위치정보가 아니라, 동일한 scene 에 대한 각 image 들의 상대적인 공간 정보라고 생각하면 될 것 같다. SLAM, structure from motion 등과 개념을 같이한다.

아래는 대표적인 NeRF 데이터셋 중 하나인 Synthetic (Blender) 데이터 중 하나의 camera pose 를 visualization 한 모습이다. 그림에서 각 blue point 들의 상대적 위치와, 기준점 대비 회전 정보 (rotation matrix) 가 제공되는 camera pose 가 된다. 우리는 각 이미지별로 공간 상에서의 상대적 위치를 알고 있으므로, 이미지 위의 점 (pixel) 들을 이에 대응하는 공간 상의 ray 로만 바꿔주면 된다. (Figure credit: BARF)

2.2. Image to Homogeneours Coordinate

우리가 먼저 해야할 것은, $z$-axis 정보가 없는 image 상의 pixel 에 대해, $z$-axis 정보를 불여넣어 2D coordinate 가 아닌 3D coordinate 로 바꿔주는 것이다. 이는 $xy$ 평면의 3D 상의 Homogeneous Coordinate 인 $z=-1$ 평면으로의 projection 을 통해서 이루어진다.

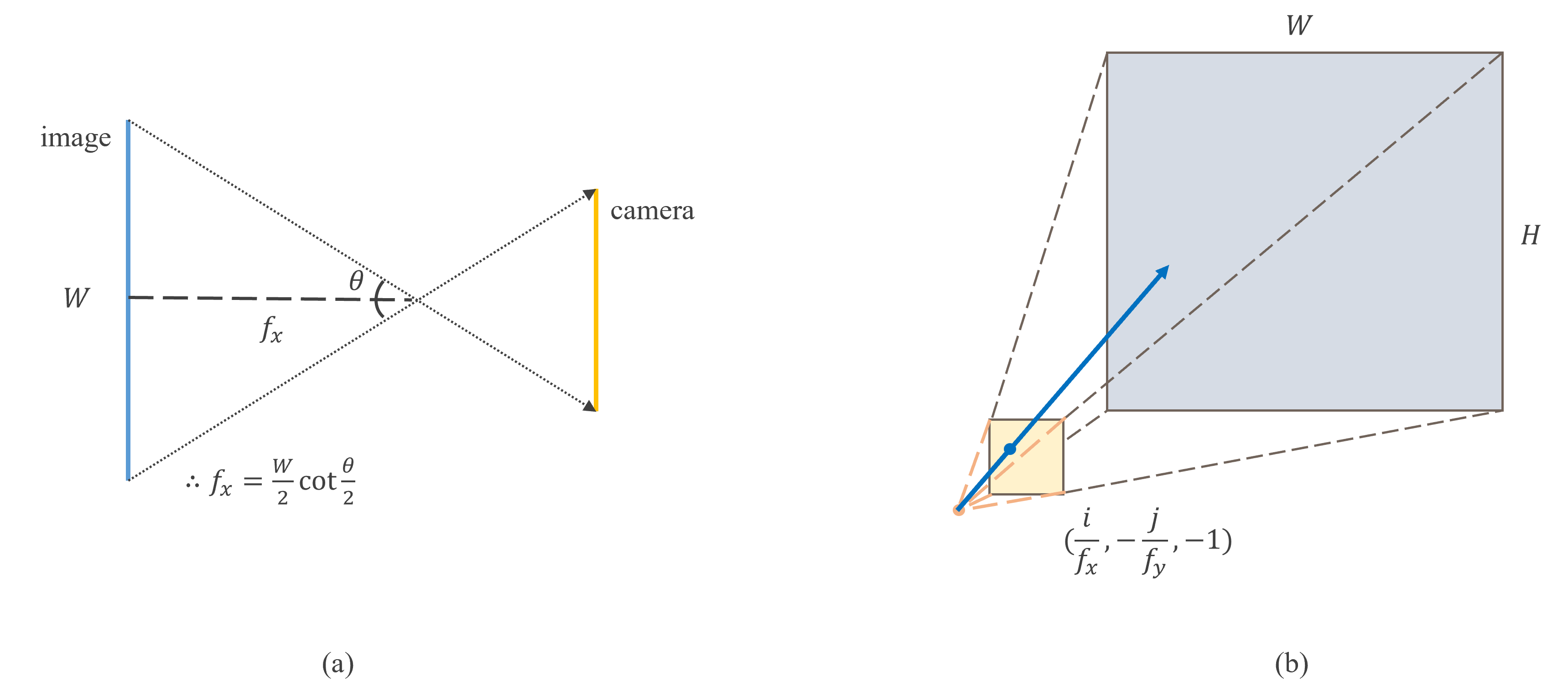
NeRF dataset 에서의 image 들은 일반적인 pinhole camera model 을 상정하기 때문에, 'transform.json' 파일을 self.transform 으로 읽었을 때, 우리가 얻게 되는 'camera_angle_x' 의 정보는 아래 그림 (a) 에서의 $\theta$ 와 같다. 따라서 우리는 focal length 를 아래 공식

을 통해 구할 수 있으며, 이는 코드로 다음과 같이 작성할 수 있다.

self.focal = 0.5*self.w / np.tan(0.5*self.transform['camera_angle_x'])

이제 우리는 image 상의 모든 pixel 에 대응하는 점을 meshgrid 를 이용하여 2D $x, y$ 좌표를 선언할 수 있으며,

x, y = np.meshgrid(
            np.arange(self.w, dtype=np.float32),  # X-Axis (columns)
            np.arange(self.h, dtype=np.float32),  # Y-Axis (rows)
            indexing='xy')

이에 대한 homogeneous coordinate $z=-1$ 위로의 projection 을 다음과 같이 작성할 수 있다.

homogeneous_directions = np.stack(
            [(x - self.w * 0.5) / self.focal,
            -(y - self.h * 0.5) / self.focal,
            -np.ones_like(x)],
            axis=-1)            

이때 $y$-axis 에 $-1$을 곱하는 이유는 pinhole camera model 이기 때문에 위 그림 (a) 와 같이 상이 뒤집혀서 맺히기 때문이다. 또한 통상적으로 이미지의 정가운데를 $(0, 0)$ 으로 설정하기 때문에 $x,y$ 좌표에 각각 이미지 width 와 height 의 절반만큼을 빼주게 된다. (0.5 를 더 빼는 경우도 있는데, 이는 성능에 큰 차이가 없는 것으로 보고된다)

이미지들의 상대적 위치를 고려하지 않는다면, 우리는 위에서 구한 homogeneous_directions $\tilde{\mathbf{d}}$ 에 대해서, image 의 pixel 에 대응되는 ray $\mathbf{r}(t)$ 를 원점 $(0,0,0)$ 을 origin 으로 하는 $\mathbf{r}(t) = t \tilde{\mathbf{d}}$ 로 나타낼 수 있을 것이다.

2.3. Homogeneous to World Coordinate

이제 우리는 모든 이미지마다 $z=-1$ 에 대응되는 3D coordinate 정보들을 알고 있으므로, 이 좌표들을 camera pose 에 대응되는 좌표들로만 바꿔주면 된다.

'transform.json' 의 transform_matrix 에 각 image 에 대응되는 Rotation matrix $\mathbf{R} \in \text{SO}(3)$, translation vector $\mathbf{t} \in \mathbb{R}^{3 \times 1}$ 이 제공되므로, 우리는 이 값을 읽어서 위에서 구한 homogeneous_directions 을 회전시키고, 원점으로부터 translation vector 만큼을 이동시키면 우리가 원하는 $\mathbf{r}(t) = \mathbf{o} + t \mathbf{d}$ 를 구할 수 있다.

이는 코드로 다음과 같이 작성할 수 있다.

c2w = self.transform['transform_matrix']

rays_d = homogeneous_directions @ c2w[:, :3].T 
rays_d = rays_d / torch.norm(rays_d, dim=-1, keepdim=True)
rays_o = c2w[:, 3].expand(rays_d.shape) 

rays_d = rays_d.view(-1, 3)
rays_o = rays_o.view(-1, 3)

1. json 파일로부터 $\mathbf{R}$ 을 읽어서 homogeneous_directions 과의 matrix multiplication 을 진행하였으며, unit direction 을 구해야 하기 때문에 이 값을 l2 norm 으로 나눠주었다.
2. origin 은 json 파일로부터 바로 translation vector 를 읽어와서 shape 만 맞춰주었다.

camera to world transform 이 $4\times4$ matrix 로 정의되기 때문에, 다음과 같이 3D world coordinate 의 homogeneous coordinate 를 이용해도 ray direction, ray origin 을 구할 수 있지만 실제 구현을 그렇게 진행하지는 않았다.

이를 통해 우리는 최종적으로 image 로부터 모든 pixel 에 대응되는 3D 상의 ray 를 구하게 되었다. 위 함수들을 이용해서 NeRF Datasets 의 get_item 함수를 작성하면 image 의 pixel 에 대응하는 data 들을 갖고 있는 Dataloader 를 불러올 수 있게 된다.

ray casting 시에는 위에서 구한 direction, origin 으로 정의되는 ray 에 곱해지는 $t$ 값을 sampling 해서 NeRF MLP 에 query 해주어 이를 accumulation (Eq.1) 하게 된다.