- Photography 가 아닌 domain 에서 Neural Rendering 을 적용하기 위해선 어떤 사항들을 고려해야하는지 생각해보자!
- Reference: SAX-NERF: Structure-aware Sparse X-Ray 3D Reconstructin, CVPR'24
- Plus: Viewer 가 없는 Neural Rendering technique 을 위한 빠른 viewer 개발 Tip
Introduction
최근 우연한 기회로 의료 도메인, 특히 Tomography (X-ray) 에서 Neural Rendering 을 어떻게 적용해야하는지 찾아볼 일이 있었다. (Ref: SAX-NeRF)
가시광의 반사를 포착하는 photography 와 다르게, tomography 는 물질을 투과한 신호를 바탕으로 이미지를 구성한다. 저자들이 Tomography 를 위해 일반적인 Neural Rendering setting 을 어떻게 수정해야 하는지를 탐구한 과정을 따라가면서, 나 또한 Neural Rendering 에 대한 추상적인 직관성과 이해를 증진시킬 수 있었다.
이 글에서는 SAX-NeRF 에 대한 개인적인 review 를 통해 Neural Rendering, NeRF, GS 등의 저변에 깔린 직관에 대해서 기술해보도록 하겠다. 아울러 official viewer 가 없을 때 viser 로 간단한 web viewer 를 만드는 tip 에 대해서도 써보려 한다.
1. Tomography vs Photography
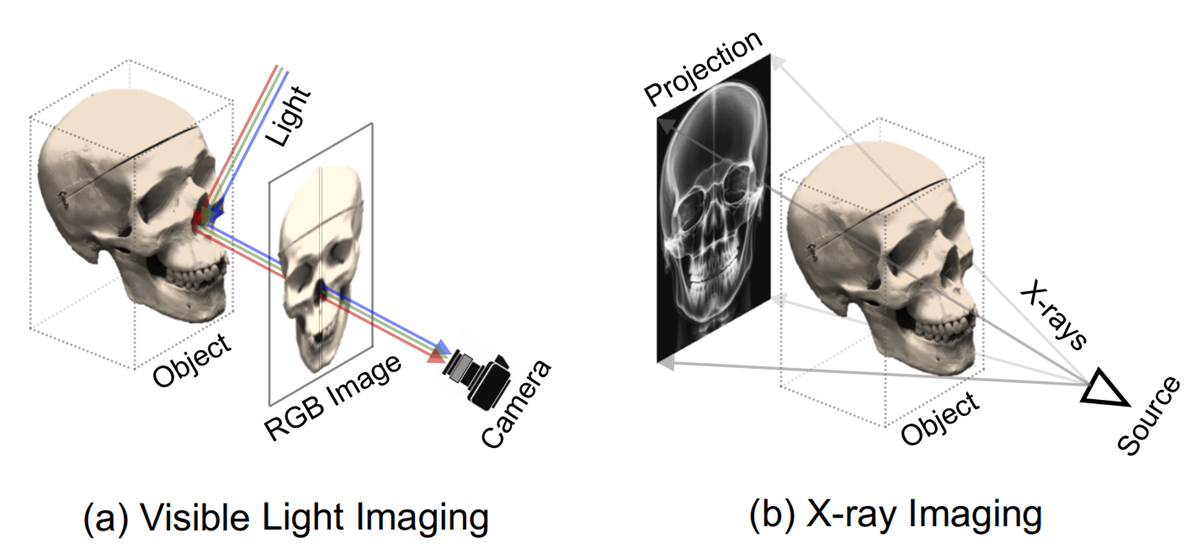
1.1. Photography
'본다'라는 행위는 물리학적으로 어떤 의미를 지닐까?
'본다'는 것은 광원에서 방출된 빛이 물체와 상호작용하여, 물체의 표면에서 특정 파장의 (or energy) 빛을 흡수하거나 반사하고, 흡수되지 않은 파장의 반사된 (reflection) 빛이 관찰자의 눈(또는 감지 장치)에 도달하여 시각적으로 인지되는 과정을 말한다.
이 과정은 빛과 물체 간의 상호작용 (흡수 및 반사), 그리고 그 상호작용의 결과가 관찰자의 시각 체계로 전달되는 과정을 포함한다.
Neural Rendering, Novel View Synthesis 에서 주로 다루는 scene 은 '가시광 영역에서 관찰한 대상' 이 목표이다. 따라서 흔히 사용하는 NeRF 의 rendering equation (emission-absortion ray casting) 은 '본다' 라는 과정의 직관을 수학적으로 나타내고 있다.
이 식에서 은 광선을 따라 누적된 최종 색을 의미한다. 각 식의 요소는 다음과 같이 해석된다:
- : 빛, 광선 (ray) 를
- : 광선이 어떤 지점 에서 물체와 상호작용 상호작용하는 밀도(opacity) 또는 흡수 계수
- : 해당 지점에서 물체가 반사하는 빛의 색 (color). (d 는 방향성을 반영하기 위해 사용하는 view-dependent color.
- : 누적 투명도, 이전에 만난 물체가 광선을 차단했는지 (불투명) 또는 통과했는지 (투명).
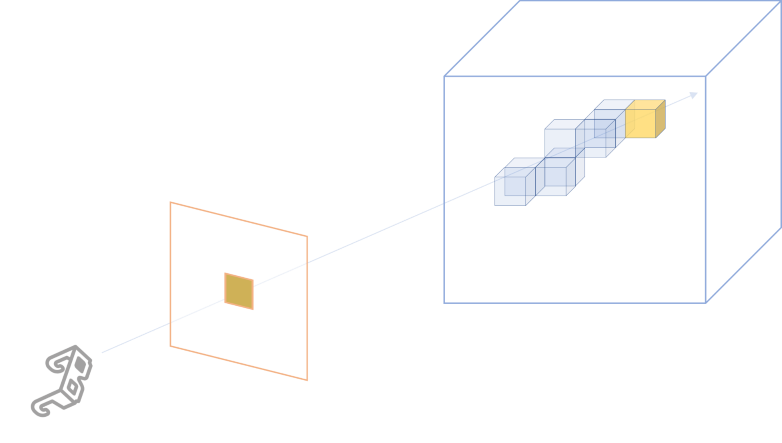
이와 같이 NeRF 의 rendering equation 은 우리가 물체를 '본다'는 행위를 수식적으로 표현한 결과물이다. 물리적 빛-물체 상호작용 (흡수, 반사, 투명도 등) 의 모든 요소를 통합하여, NeRF는 광선 경로를 따라 누적된 빛의 기여를 계산해 최종적으로 이미지를 생성한다.

1.2. Tomography
그렇다면 Neural Rendering 을 가시광 영역이 아닌 domain 에 적용하려면 어떻게 해야할까?
해당 domain 의 대표적이면서 대중적인 예시가 X-ray, CT 등으로 익숙한 Tomography 일 것이다. Tomgraphy 는 가시광선보다 파장이 짧은 (에너지가 큰) X-ray 를 사용하여 빛이 반사되기보다는, 물체를 투과 (penetration)하고, 빛의 세기가 물체 내부의 밀도에 의해 감쇠 (attenuation)되는 과정을 기반으로 한다. 이 과정은 가시광선 기반의 Reflection과 대비되며, 빛이 물체의 뒤쪽에 맺히는 상 (intensity)을 분석하여 물체의 내부 구조를 재구성한다.

Tomography 에서 이러한 penetration, attenuation 과정을 modeling 하는 식은 Beer-Lambert Law 로 표현되는데, 구체적으로는 다음과 같다.
- 여기서 는 상에 맺힌 최종적인 intensity, 는 initial intensity 값이다.
- 는 radiodensity 값으로, X-ray 가 attenuation 되는 정도를 나타낸다.
exponential 항이 익숙하지 않은가? NeRF modeling 에서 사용하는 Accumulated Transmittance 수식과 똑같은 형태를 지니고 있다. 실제로 두 항은 Intensity 가 감소하는 정도가 1) 현재 지점 빛의 세기, 2) 현재 지점의 불투명도에 비례할 것이라는 동일한 가정을 지니고 있다.
다음과 같은 유도 과정을 통해서도 이 modeling 의 저변에 빛의 intensity 에 대한 직관성이 담겨있는 것을 알 수 있다.
- Derivation of Beer-Lambert Law (as same as the Accumulated Transmittance)
이 유도 과정은 빛의 감쇠가 현재 빛의 세기와 밀도에 비례한다는 기본적인 물리적 직관을 보여주며, 이는 NeRF의 투명도 개념과 유사한 방식으로 이해될 수 있음을 시사한다.
Tomography 를 입력으로 하는 NeRF 를 reconstruction 하기 위해서는, 기존 emission-absorption ray casting 대신에 위의 Beer-Lambert Law 기반으로 rendering equation 을 대체해야 할 것이다.
최종적인 intensity rendering term 은 NeRF 에서처럼 discretized form 으로 다음과 같이 표현된다.
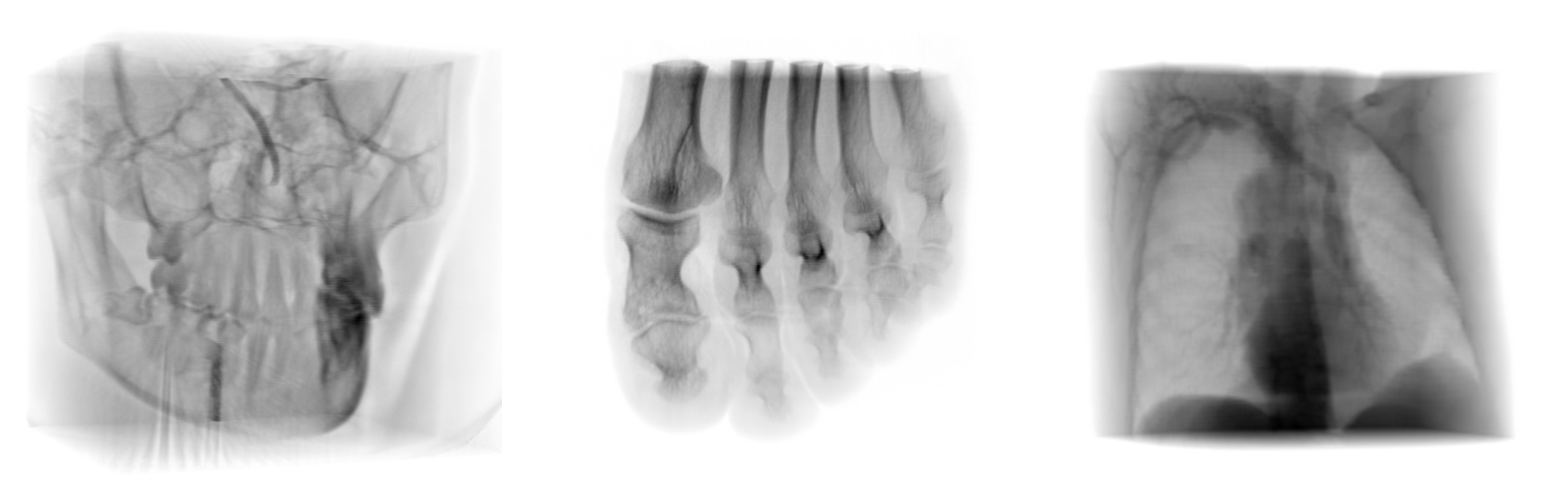
2. Modeling
다시 NeRF 로 돌아가보자.
Hash Grid NeRF, TensoRF 등의 변형이 있지만, 기본적으로 NeRF 의 골자는 어떠한 3D scene 을 parameterize 해서 표현하자는 것이다.
이 parameterization 의 방법이 MLP 라면 NeRF 계열이, explicit 한 3D Gaussian, 2D Gaussian surfel 등을 사용하면 Gaussian Splatting 계열이 될 것이다.
일반적으로 이러한 parameter model 은 3D Cartessian Coordinate 을 입력으로 받아 그 점의 density 와 color 를 출력하도록 modeling 된다.
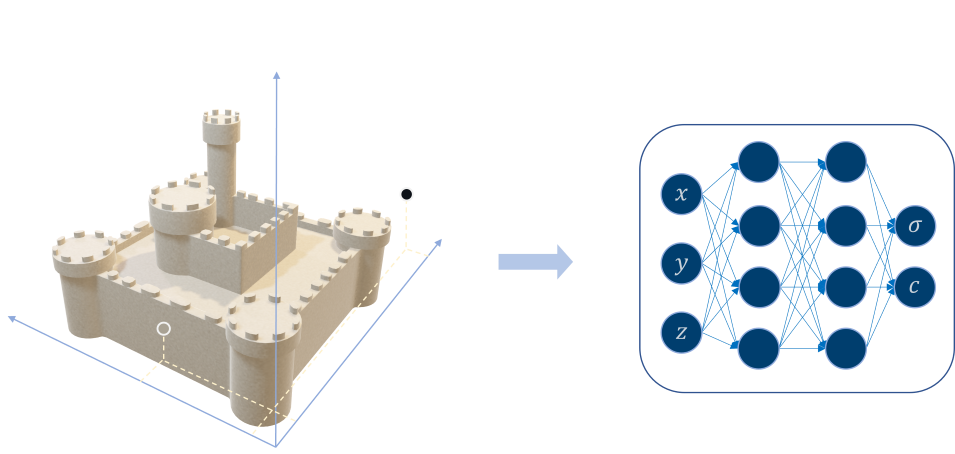
하지만 Tomography 의 rendering equation 에서는 가 아닌 radiodensity 가 필요하므로, Tomography 에 NeRF 를 적용하려면, Photography 와 다른 방식으로 모델링해야 한다.
Beer-Lambert Law 를 바탕으로 수정된 Tomography 의 rendering equation 은 radiodensity 에만 dependent 하므로, Tomography-NeRF 또한 3D Cartessian Coordinate 을 입력으로 받아 하나만을 출력하게 하는 구조로 바꿔주면 된다.
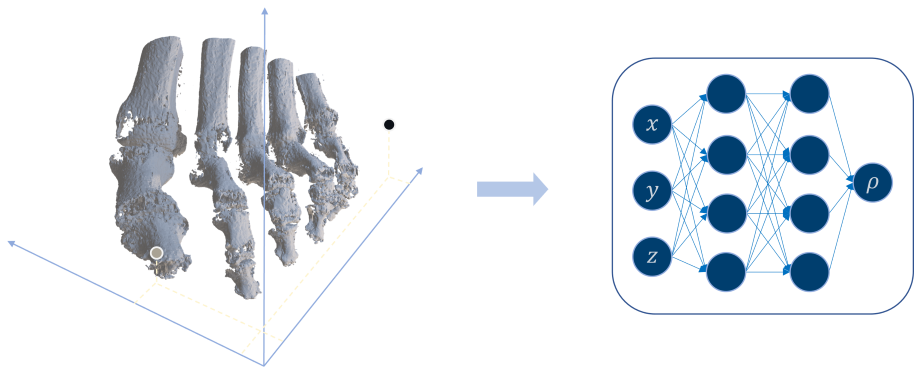
SAX-NeRF 에서는 이후 X-Ray 특성을 고려해서 MLP 를 적용하기보단, Transformer 로 바꿔주고 attention 안에서 ray 간 locality inductive bias 를 고려하는 설계 등을 제시하긴 한다. 하지만 크게 중요한 부분은 아니라고 생각해서 스킵하도록 하겠다. 궁금하면 논문을 참조하길 바란다.
3. 빠른 Neural Rendering Viewer 개발 Tip
3.1. Viser Viewer
SAX-NeRF 는 code 가 공개되어 있긴 하지만, official viewer 가 없고 visualization 으로 제공하는 기본 코드가 제한적이라 결과를 좀 더 interactive 하게 살펴보기 위해서는 viewer 를 구현할 필요가 있었다.
Q. NeRF / GS model 을 interactive 하게 '보기' 위해서는 어떤 요소들이 필요할까?
- 3D scene 을 관찰하려는 각도의 정보 ()
- 각도를 통해 생성한 rays
- Rendering (rendering equation 적용)
대게의 경우 2), 3) 은 코드가 공개되어 있는 상태라면 참고해서 구현하는 것이 어렵지는 않다. 하지만 camera coordinate system 은 project 마다 다른 경우, 특히 OpenGL <-> OpenCV 의 coordinate system 이 달라서 오류가 나는 경우가 많으므로 구현하려는 project 에 맞춰서 ray 를 생성해야 한다.
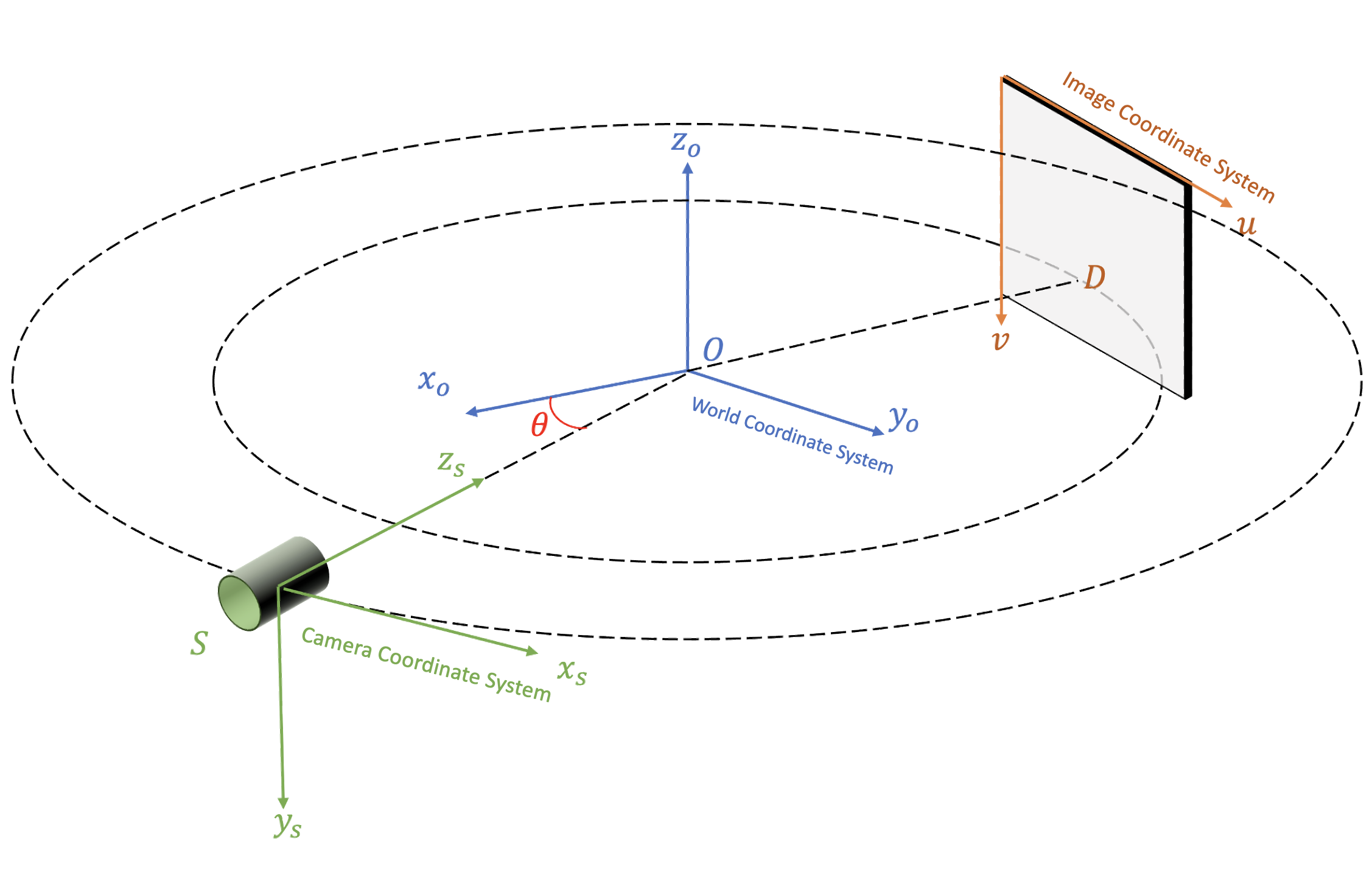
또다른 문제는 1) 을 custom 하게 구현해서 원하는 대로 scene 을 컨트롤 하기가 좀 힘들다는데 있는데, 다행히도 NeRFStudio team 이 개발 중인 viser 를 이용하면 이 부분을 굉장히 쉽게 해결할 수 있다. 예전에 개발했던 2D Gaussian Spaltting 용 viewer 도 이 viser 를 이용한 project 이다.
아래는 viser 를 이용해서 구현한 아주 간단한 SAX-NeRF viewer 이다. 아래 구현에서는 viser project 중에서도 minimal 한 feature 를 제공하고 잇는 nerfview package 를 이용하였다.
- Installation
pip install nerfview- Source Code:
viewer.py
from typing import Tuple
import time
import viser
import nerfview
import tyro
import os
import torch
import numpy as np
import argparse
import matplotlib.pyplot as plt
from src.network import get_network
from src.encoder import get_encoder
from src.config.configloading import load_config
from src.render import render
def normalize(img):
max_val = img.max()
min_val = img.min()
return (img - min_val) / (max_val - min_val)
@torch.no_grad()
def make_rays(K, c2w, img_wh, dsd=1.5, device='cuda'):
H, W = img_wh
pose = create_sax_pose_from_camera(c2w, DSO=1.0)
i, j = torch.meshgrid(torch.linspace(0, W - 1, W, device=device),
torch.linspace(0, H - 1, H, device=device), indexing="ij")
uu = (i.t() + 0.5 - W / 2) * 0.001
vv = (j.t() + 0.5 - H / 2) * 0.001
dirs = torch.stack([uu / dsd, vv / dsd, torch.ones_like(uu)], -1)
rays_d = torch.sum(torch.matmul(pose[:3,:3], dirs[..., None]).to(device), -1)
rays_o = pose[:3, -1].expand(rays_d.shape)
rays = torch.cat([rays_o, rays_d,
torch.full_like(rays_o[..., :1], 0.904),
torch.full_like(rays_o[..., :1], 1.1)], dim=-1)
return rays.reshape(-1, 8)
@torch.no_grad()
def create_sax_pose_from_camera(c2w: torch.Tensor, DSO: float):
forward_vector = c2w[:3, 2]
angle = np.arctan2(forward_vector[1], forward_vector[0])
phi1 = -np.pi / 2
R1 = np.array([[1.0, 0.0, 0.0],
[0.0, np.cos(phi1), -np.sin(phi1)],
[0.0, np.sin(phi1), np.cos(phi1)]])
phi2 = np.pi / 2
R2 = np.array([[np.cos(phi2), -np.sin(phi2), 0.0],
[np.sin(phi2), np.cos(phi2), 0.0],
[0.0, 0.0, 1.0]])
R3 = np.array([[np.cos(angle), -np.sin(angle), 0.0],
[np.sin(angle), np.cos(angle), 0.0],
[0.0, 0.0, 1.0]])
rot = np.dot(np.dot(R3, R2), R1)
trans = np.array([DSO * np.cos(angle), DSO * np.sin(angle), 0])
# rot = c2w[:3, :3].T
# trans = np.array([DSO, DSO, 0])
pose = np.eye(4)
pose[:-1, :-1] = rot
pose[:-1, -1] = trans
return torch.tensor(pose, dtype=torch.float32, device='cuda')
class NerfViewer:
def __init__(self, args):
self.args = args
os.environ["CUDA_DEVICE_ORDER"] = 'PCI_BUS_ID'
os.environ["CUDA_VISIBLE_DEVICES"] = args.gpu_id
self.cfg = load_config(args.config)
self.device = torch.device("cuda")
self.dsd_value = 1.5
self.clm_colors = torch.tensor(plt.cm.get_cmap("turbo").colors, device="cuda")
self.network = get_network(self.cfg["network"]["net_type"])
self.cfg["network"].pop("net_type", None)
self.encoder = get_encoder(**self.cfg["encoder"])
self.model = self.network(self.encoder, **self.cfg["network"]).to(self.device)
self.model_fine = None
n_fine = self.cfg["render"]["n_fine"]
if n_fine > 0:
self.model_fine = self.network(self.encoder, **self.cfg["network"]).to(self.device)
ckpt = torch.load(args.weights)
print(ckpt["epoch"])
self.model.load_state_dict(ckpt["network"])
if n_fine > 0:
self.model_fine.load_state_dict(ckpt["network_fine"])
self.model.eval()
self.render_W = args.size
self.render_H = args.size
@torch.no_grad()
def render_fn(self, camera_state: nerfview.CameraState, img_wh: Tuple[int, int]) -> np.ndarray:
W, H = img_wh
render_img_wh = (self.render_W, self.render_H)
c2w = camera_state.c2w
K = camera_state.get_K(img_wh)
rays = make_rays(K, c2w, render_img_wh, self.dsd_value, device=self.device)
chunk_size = 1048576
num_rays = rays.shape[0]
all_imgs = []
for i in range(0, num_rays, chunk_size):
start = i
end = min(i + chunk_size, num_rays)
rays_chunk = rays[start:end]
rendered_chunk = render(rays_chunk, self.model, self.model_fine, **self.cfg["render"])["acc"]
all_imgs.append(rendered_chunk)
img = torch.cat(all_imgs, dim=0).reshape(self.render_H, self.render_W, 1)
img = img.repeat(1, 1, 3)
img = torch.nn.functional.interpolate(img.unsqueeze(0).permute(0, 3, 1, 2), size=(H, W), mode='bilinear', align_corners=False).squeeze(0).permute(1, 2, 0)
img = (normalize(img.cpu().numpy()) * 255).astype(np.uint8)
return img
def update_dsd(self, value):
self.dsd_value = value
def config_parser():
cat = 'foot'
parser = argparse.ArgumentParser()
parser.add_argument("--gpu_id", default="0", help="gpu to use")
parser.add_argument("--method", default=f"Lineformer", help="name of the tested method")
parser.add_argument("--category", default=f"{cat}", help="category of the tested scene")
parser.add_argument("--config", default=f"config/Lineformer/{cat}_50.yaml", help="path to configs file")
parser.add_argument("--weights", default=f"pretrained/{cat}.tar", help="path to the experiments")
parser.add_argument("--output_path", default=f"output", help="path to the output folder")
parser.add_argument("--vis", default="True", help="visualization or not?")
parser.add_argument("--size", default=256)
return parser
def main(args):
nerf_viewer = NerfViewer(args)
with torch.no_grad():
server = viser.ViserServer(verbose=True, port=9123, )
_ = nerfview.Viewer(server=server, render_fn=nerf_viewer.render_fn, mode='rendering')
dsd_val = server.add_gui_slider(
"DSD",
min=0.1,
max=2.0,
step=0.05,
initial_value=nerf_viewer.dsd_value,
)
@dsd_val.on_update
def _(_) -> None:
nerf_viewer.update_dsd(dsd_val.value)
while True:
time.sleep(1.0)
if __name__ == "__main__":
parser = config_parser()
args = parser.parse_args()
tyro.cli(lambda: main(args))- Usage
python viewer.py- Still Shot
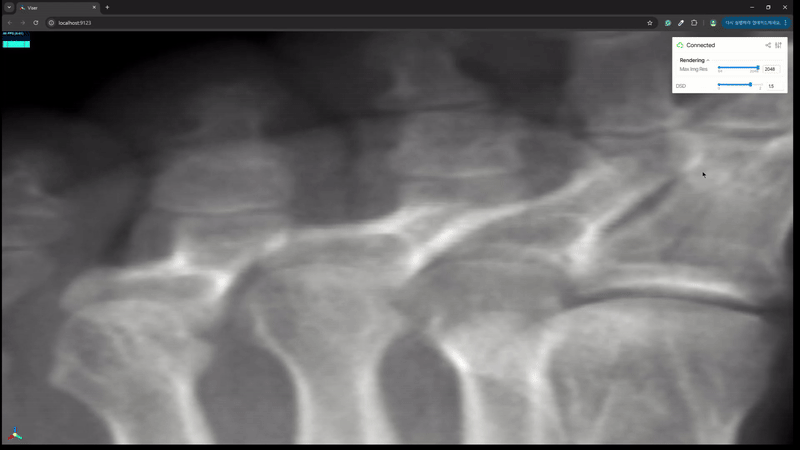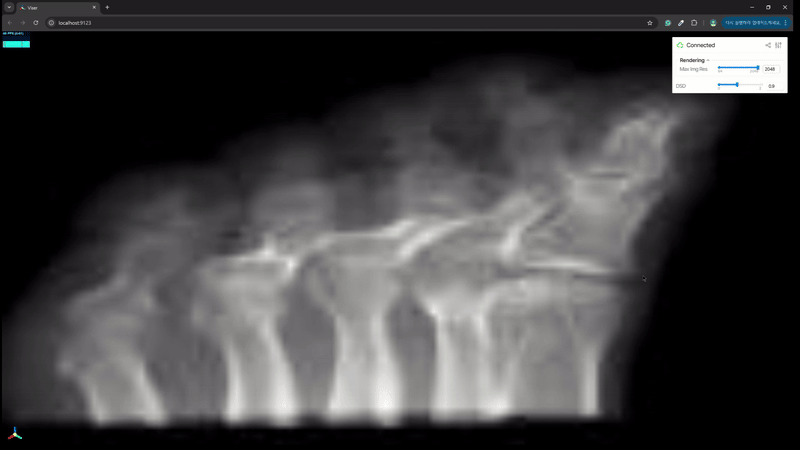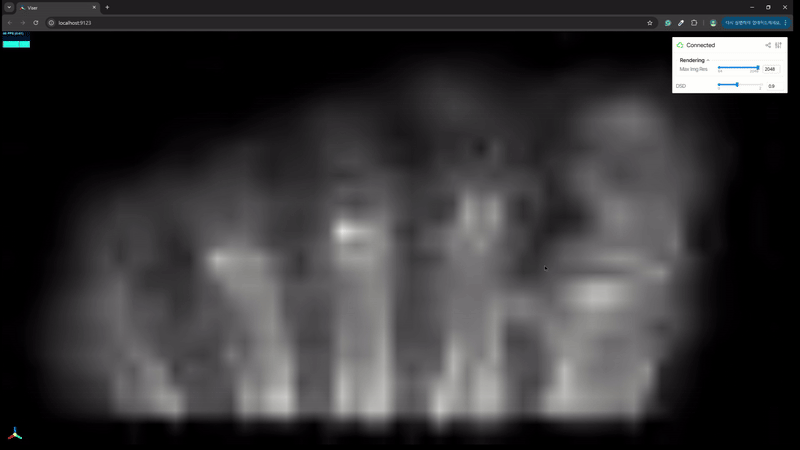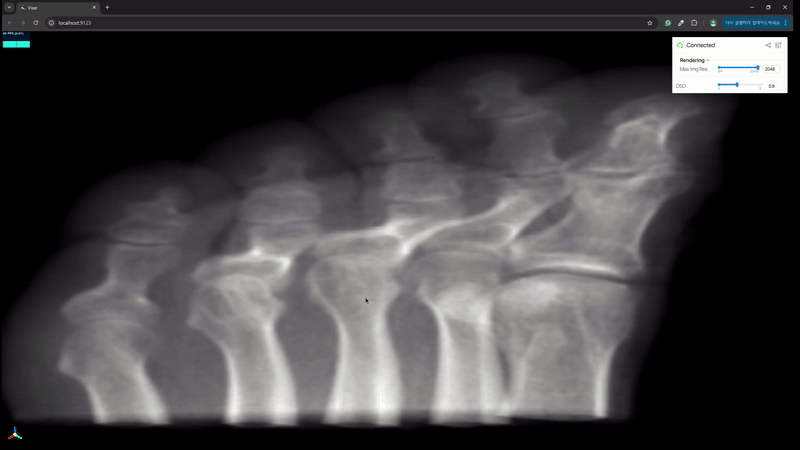
이처럼 간단한 코딩으로 새로운 NeRF / GS 모델에 대한 viewer 를 빠르게 만들 수 있다. 원래는 github 에 올릴까 하다가 너무 간단한 코딩이라 블로그에만 올리고 갈무리하려 한다.
3.2. Marching Cube Extraction
또 하나 NeRF / GS scene 을 interactive 하게 확인하는 방법은, marching cube 등의 scalar field -> polygonal mesh 변환 알고리즘을 이용하는 것이다.
하지만 분명히 할 점은, 2D GS, SDF 처럼 surface reconstruction 에 특화되지 않은 모델이라면 일반적인 NeRF 나 GS 는 conventional 한 mesh conversion 알고리즘에 그렇게 잘 맞지는 않는다는 점이다.
어디까지나 참고로 활용해보면 좋을 것.
아래는 SAX-NeRF 에서 간단하게 mesh 를 생성하는 코드 Example 이다.
- 의 voxel 을 선언하고 voxel 안의 모든 point 를 NeRF 에 쿼리하여 occupancy grid 를 만듬
- marching cube 적용하여 polygonal mesh 로 변환
from skimage import measure
import trimesh
from src.config.configloading import load_config
from src.network import get_network
from src.encoder import get_encoder
from src.render import render, run_network
# init model
'''
load SAX NeRF model, see: test.py in SAX-NeRF
'''
# make voxel
voxel_size = 128
x, y, z = np.mgrid[:voxel_size, :voxel_size, :voxel_size]
x = (x - (voxel_size - 1) / 2) / (voxel_size / 2)
y = (y - (voxel_size - 1) / 2) / (voxel_size / 2)
z = (z - (voxel_size - 1) / 2) / (voxel_size / 2)
voxel = np.stack([x, y, z], axis=-1)
voxel /= 16
# marching cube
threshold = 0.4
voxel_estimated = run_network(voxel, model_fine if model_fine is not None else model, netchunk)
voxel_estimated = voxel_estimated.squeeze(dim=-1).cpu().numpy()
verts, faces, _, _ = measure.marching_cubes(voxel_estimated, level=threshold)
mesh = trimesh.Trimesh(vertices=verts, faces=faces)
mesh.export("output.obj")


안녕하세요! 좋은 포스트 정말 감사합니다. 그런데 썸네일 이미지에 image plane이 camera coordinate 기준이 아닌 world coordinate을 기준으로 표현된 것 같은데, 그러한 표현에도 의미가 있는지 여쭤볼 수 있을까요? Pinhole camera를 생각했을 때 coordinate은 world를 기준으로 잡더라도, camera의 principal plane과 평행하게는 그려져야하는게 아닌가 해서 여쭤보고자 합니다.