개요

두 수의 최대공약수를 구할 때, '유클리드 호제법'을 사용하면
간편하게 구현할 수 있다.

최대공약수를 구하는 법

소인수분해

1112 = 139 X 2 X 2 X 2
695 = 139 X 5
==> 최대공약수(GCD): 139

• 소인수분해 방법은 수가 커질수록 어려워지는 단점이 있다.

유클리드 호제법

• x와 y의 최대공약수는 y, r의 최대공약수와 같다는 원리를 이용
  • r = x%y
• 위 방법을 반복한다.

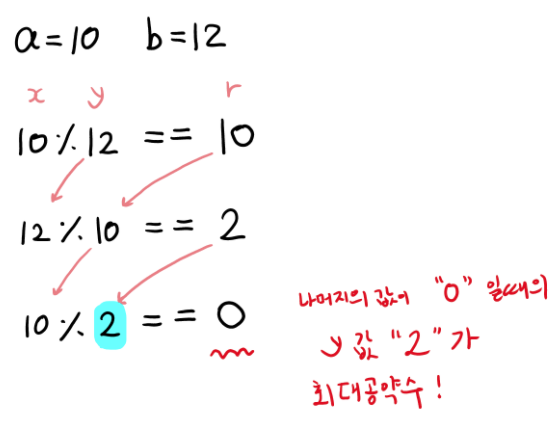
유클리드 호제법 증명

위의 방법으로 신기하게도 최대공약수가 구해지는 것은 알겠지만,
도대체 어떻게 되는건지 이해가 안돼서 증명을 찾아보았다.

• 조건
  • a>b인 두 양의 정수 a,b를 정함
  • 최대공약수를 G라고 정의
  • $a=AG$,   $b=BG$
  • Key point: A와 B는 서로소이다.
    (A,B가 서로소가 아니면 G는 최대공약수가 아님.. ㅋㅋ)
• 풀이
  • a>b이므로 a를 b로 나눈다
    • $a = qb + r$ (q:몫, r: 나머지)
    • 위 식에 $a=AG$,   $b=BG$ 대입
    • $AG= qBG + r$
      = $AG- qBG = r$
      = $G(A- qB) = r$
  • 따라서, $r=(A- qB)G$,   $b=BG$이므로
    r과 b 사이에도 G라는 공통의 약수가 생기는 것을 알 수 있다!
  • 즉 (A-qB)와 B가 서로소임을 증명하면, 유클리드 호제법을 증명할 수 있다.
• 서로소 증명
  • 서로소임을 귀류법을 사용해서 증명해보자
    가정: (A-qB)와 B가 서로소가 아니다
  • $A-qB=mt$,   $B=nt$
    (두 수가 서로소가 아니라고 가정했으므로, 최대공약수 t가 존재한다고 생각할 수 있음)
  • $A-qnt=mt$
    $A=mt+qnt=t(m+qn)$
    즉, $A=mt+qnt=t(m+qn)$,   $B=tn$이므로 A,B가 서로소가 아닌 것을 알 수 있다.
  • 우리가 위에서 Key point라고 했던 부분을 보면
    A와 B는 서로소라고 했었다.
    하지만 귀류법을 사용해서 (A-qB)와 B가 서로소가 아니라고 가정했을 경우, Key point였던 A, B가 서로소라는 가정이 위배가 된다.
    따라서, 위에서 가정했던 (A-qB)와 B가 서로소가 아니다는 틀린 말이 되며,
    (A-qB)와 B는 서로소라는 것을 알 수 있다.

참고

• 알로호모라
• yerin4847
• yuseong40