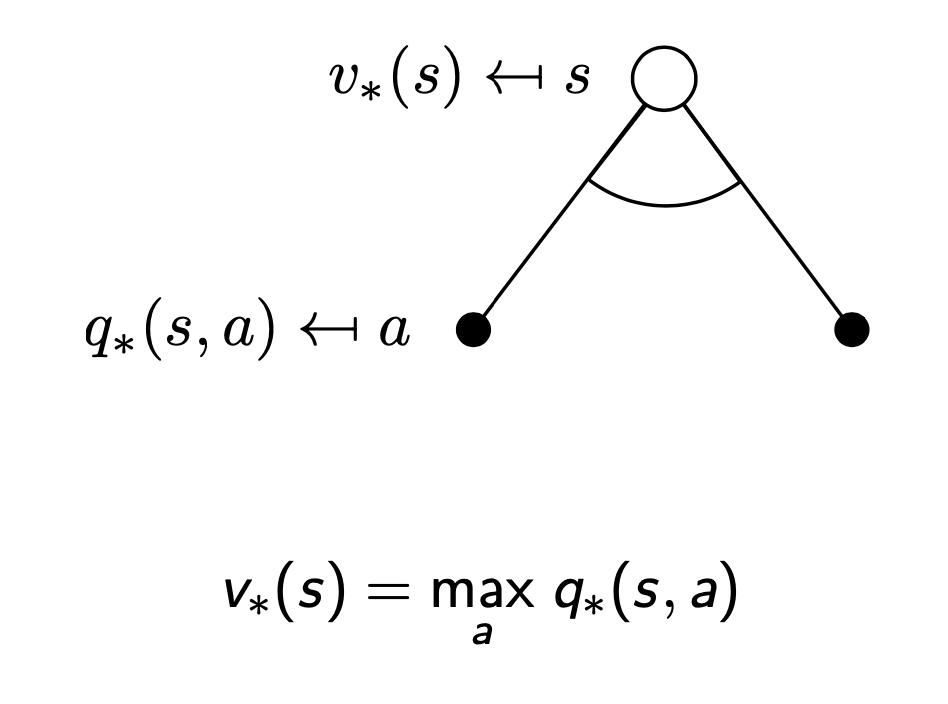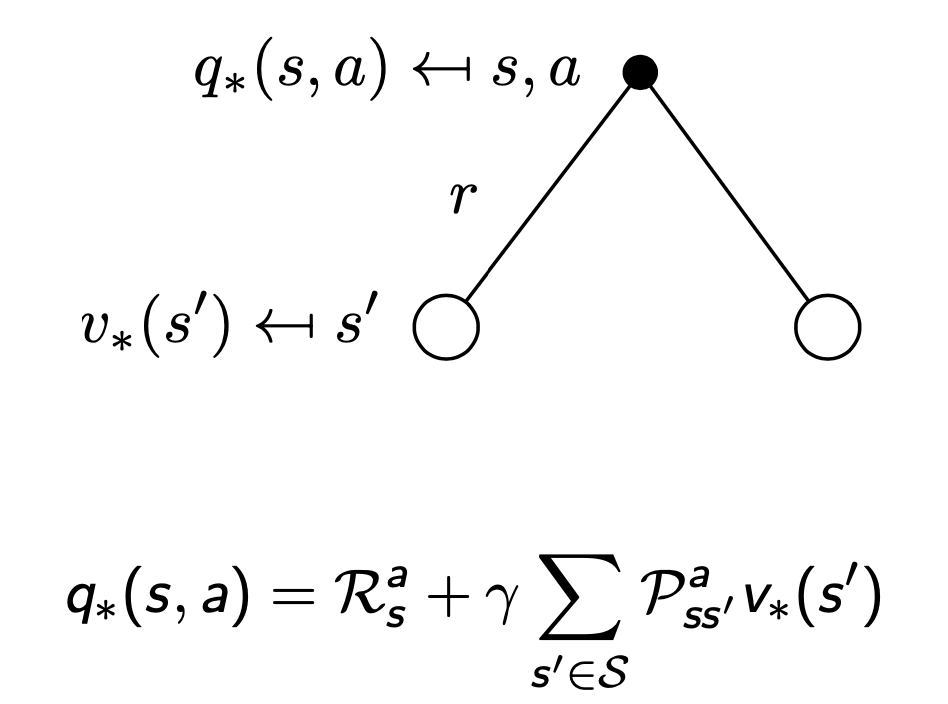David Silver 교수님의 RL Course 강의 내용 정리
Lecture 2: Markov Decision Process
Markov Process
Markov Property (마르코프 성질)

- Markov: 미래 상태는 오직 현재에 의해 결정됨
- The state captures all relevant information from the history
- state가 알려지면 history는 불 필요함
- Markov한 상태 예시 --> 체스 게임
현재 두어야하는 최선의 수는, 현재 체스판의 상태를 보고 정해야함 (이전에 어떤 수를 두었는지는 관련이 없음)
State Transition Matrix
-
상태전이확률: --> 로 전환될 확률을 의미
- State transition probability
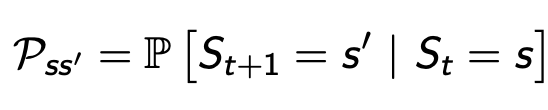
- State transition probability
-
상태전이행렬: 모든 상태 에서 상태 의 상태전이확률 행렬
- State transition matrix
- 각 행의 합은 1
- ex. --> => 확률
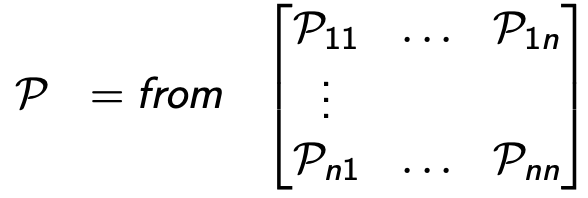
Markov Process

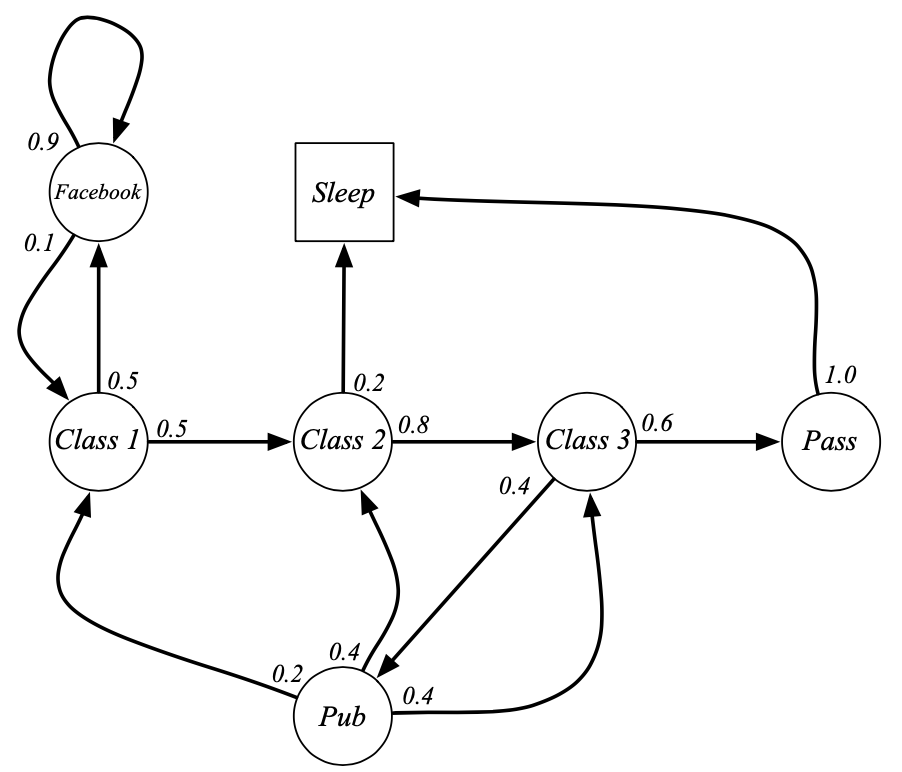
- Markov Process는 S(상태)와 P(상태전이확률)의 tuple
- memorlyless: 어느 경로에서 오든, 현재 상태(State)에서 미래가 정의된다는 것 (Markov property)
- environment가 모두 관측 가능한 상황
- 미리 정의된 어떤 확률 분포를 따라서 상태와 상태 사이를 이동하는 여정
- 어떤 상태에 도착하면 그 상태에서 다음 상태가 어디가 될지 각각 해당하는 확률이 있고, 그 확률에 따라 다음 상태가 정해지는 것
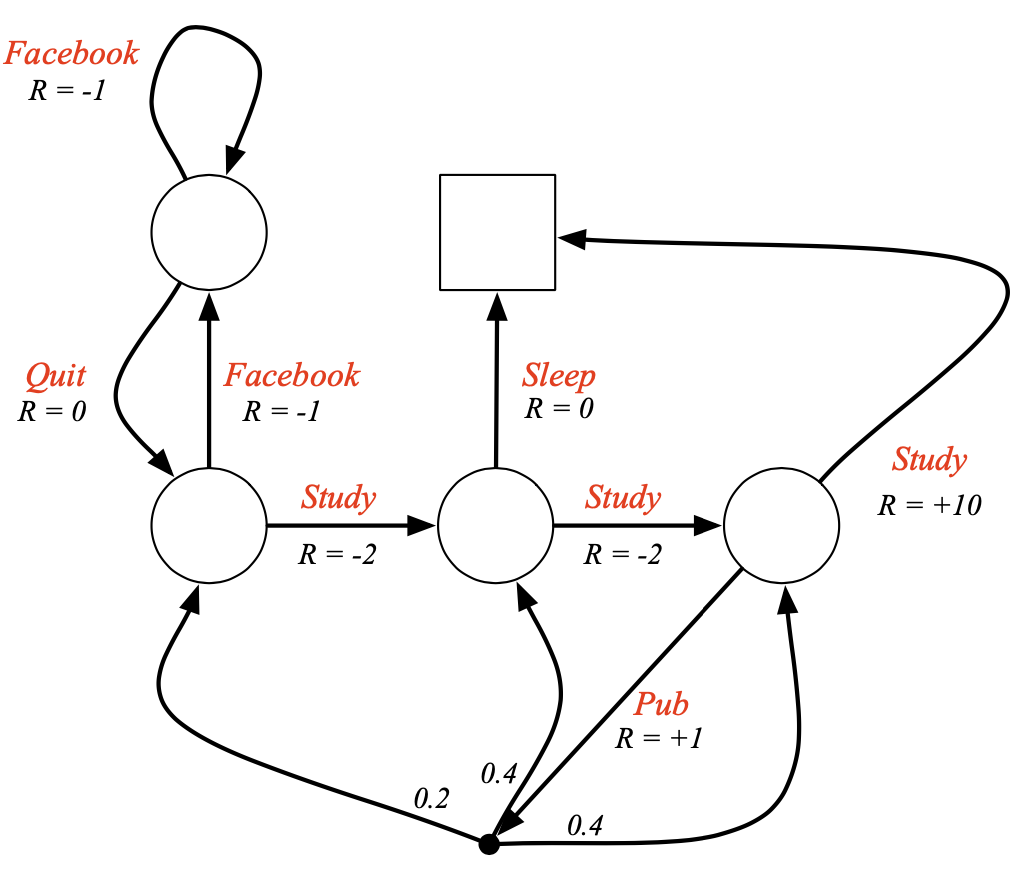
- 예시
- episode1: C1 > C2 > C3 > Pass > Sleep (종료)
- episode2: C1 > FB > FB > C1 > C2 > Sleep (종료)
- 상태전이행렬
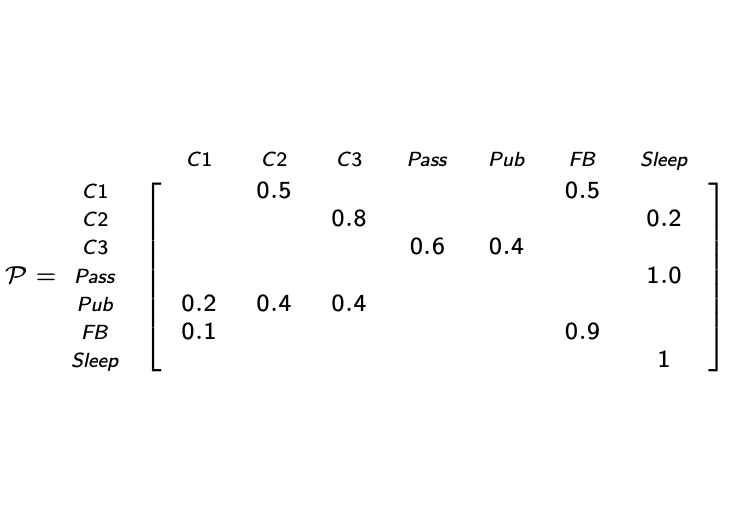
Markov Reward Process

- Markov Reward Process는 S,P,R,의 tuple
- : 상태 에서 받을 수 있는 t+1 시점의 보상(기댓값)
- : 할인율,
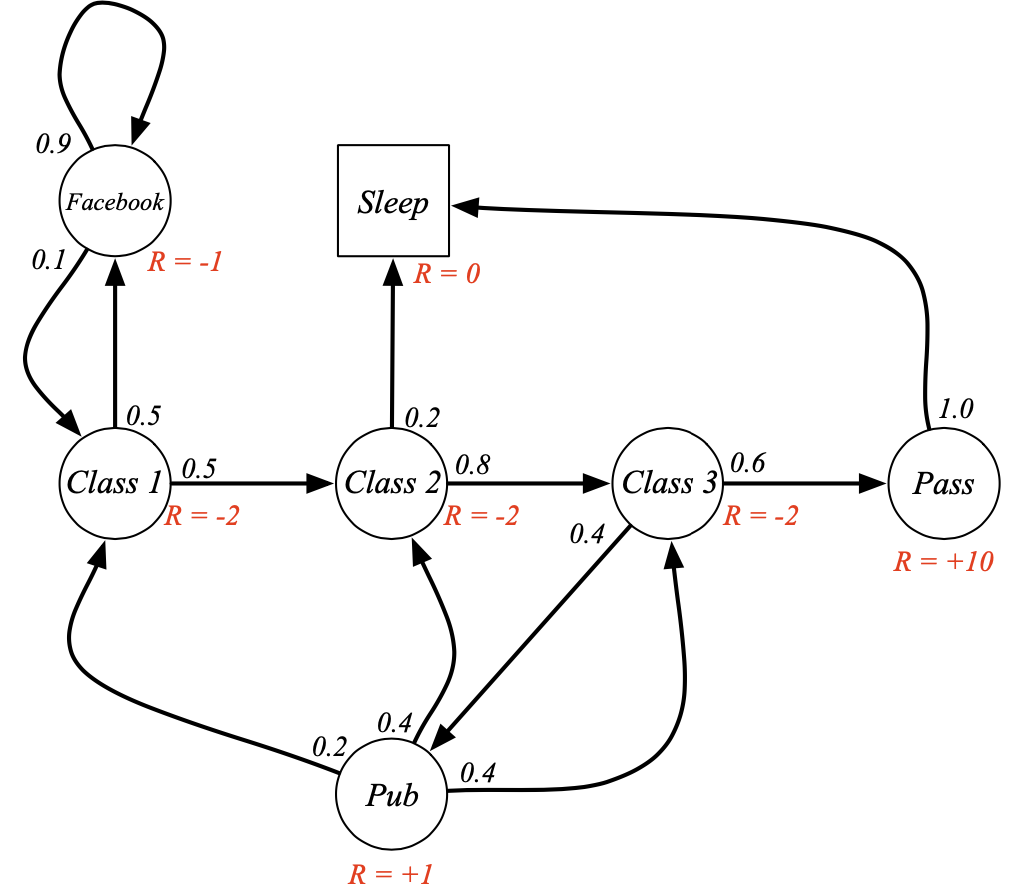
Return
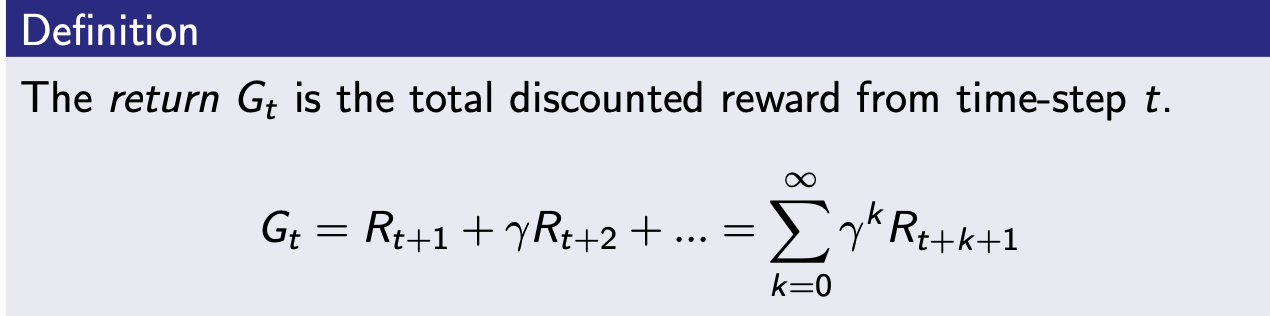
- return: , t시점의 보상의 총합 (미래시점의 보상들은 할인율을 적용)
- 목표: 를 maximize하는 것
- 할인율: 미래 보상을 현재 값으로 변환하는 값
- 수학적으로 편리함 (avoid infinite returns, 수렴이 증명됨)
- 사람/동물이 즉각적인 보상을 더 선호하는 것을 반영
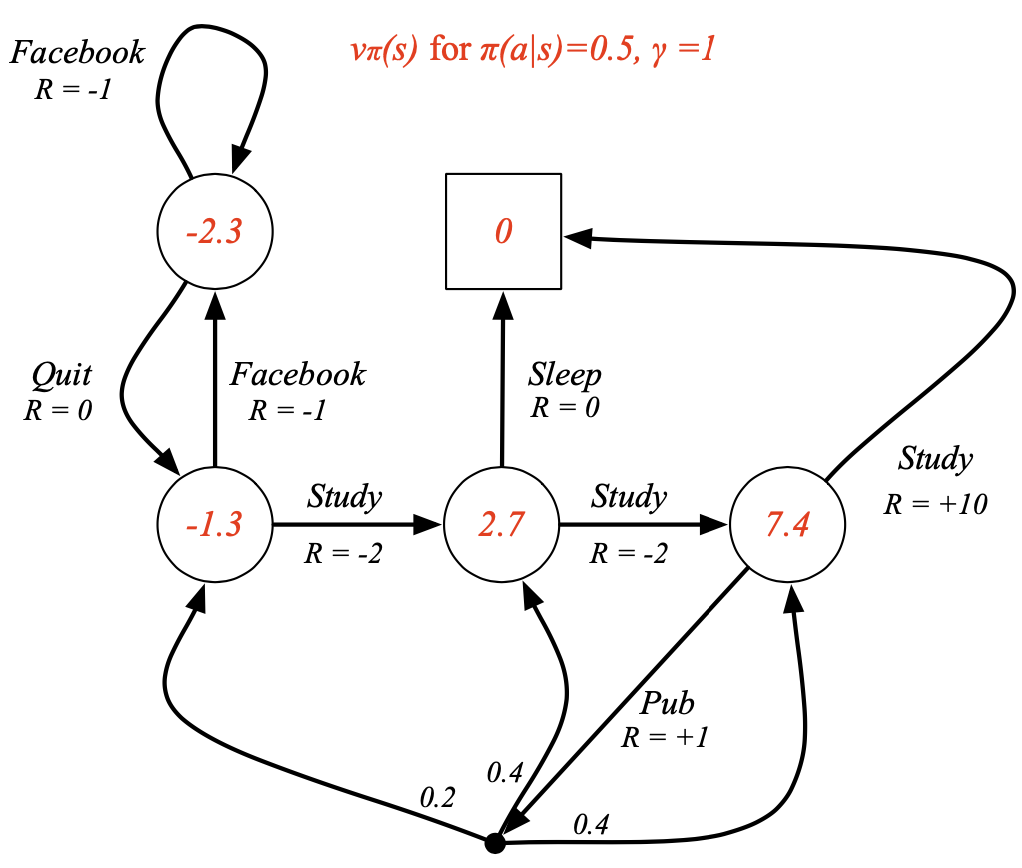
State Value Function (상태가치함수)
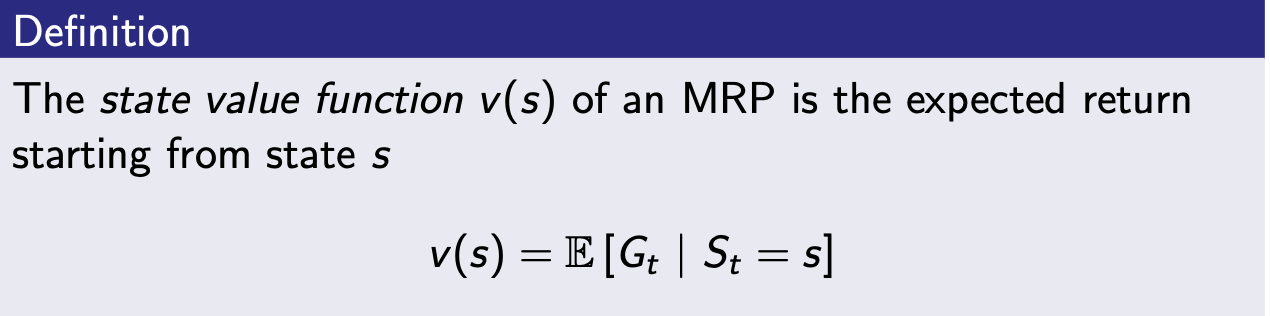
- : 상태에서 앞으로 받을 보상의 합을 출력하는 함수
- agent는 가치함수를 통해 어떤 상태에 있는 것이 얼마나 좋은지 알 수 있음
- 예시 ( = 0)
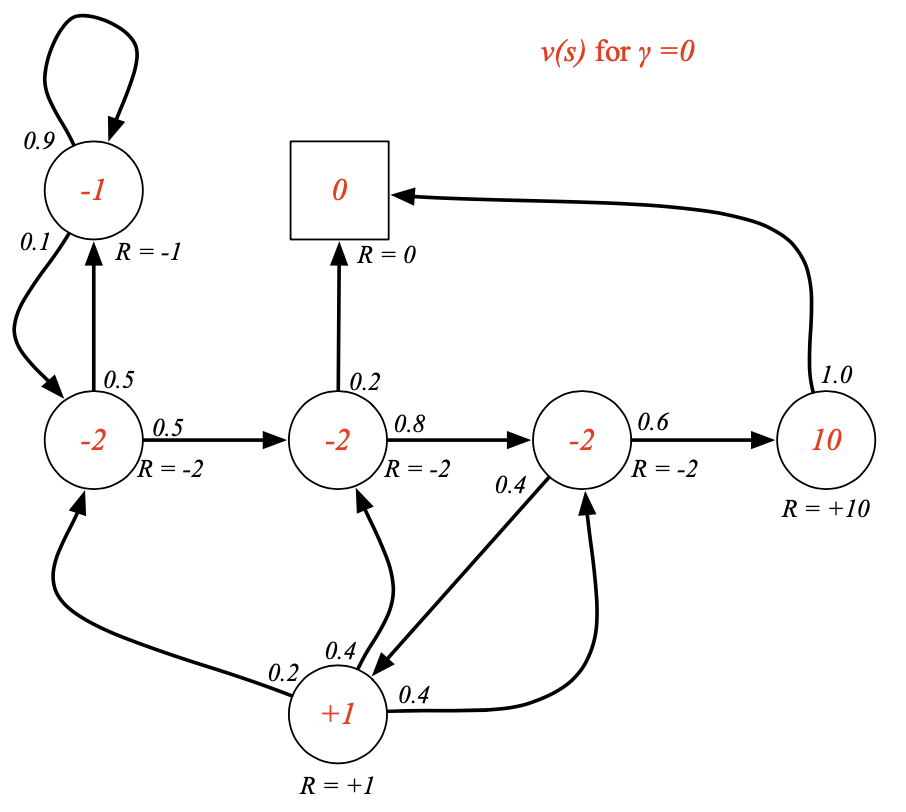
Bellman 방정식
- 현재 상태의 가치함수와 다음 상태 가치함수의 관계식
- discounted value of successor state
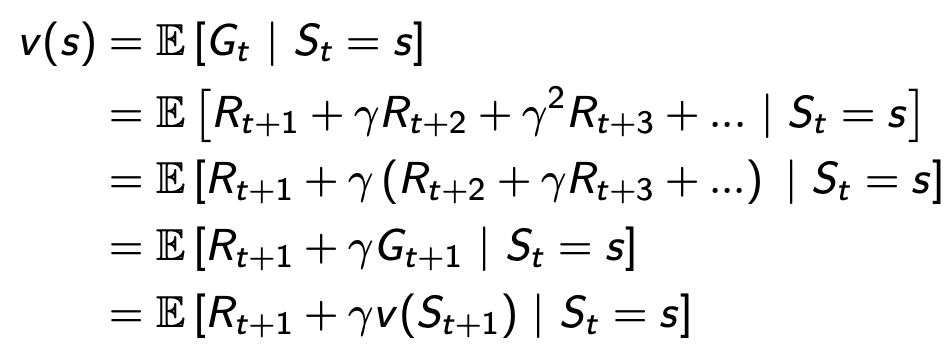
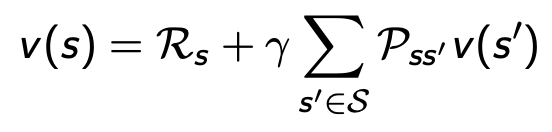
-
예시
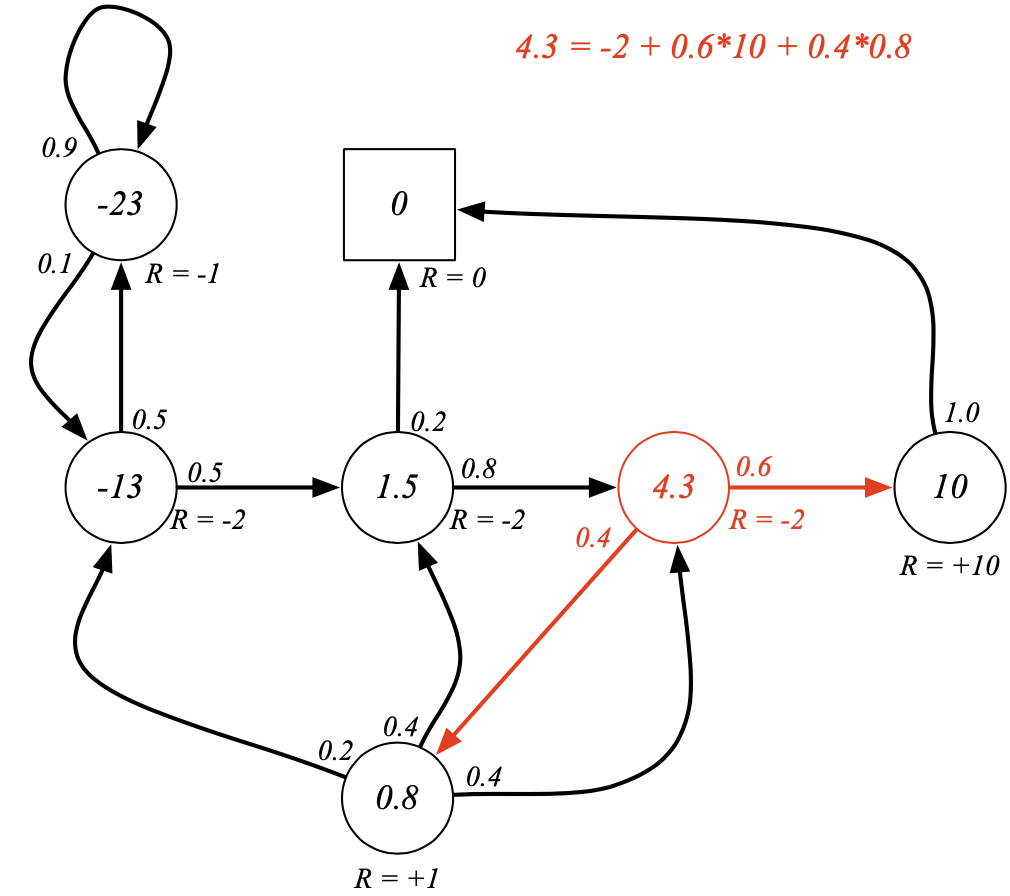
-
간결식:
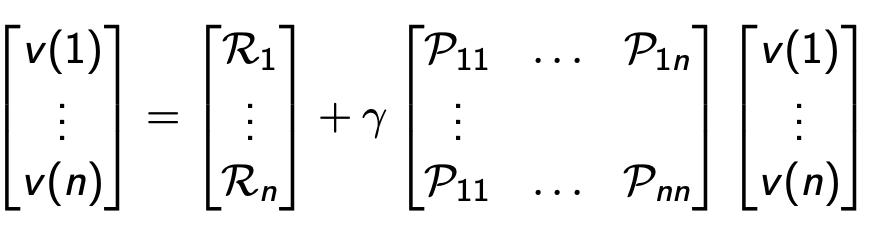
-
Direct solution
- 계산복잡도:
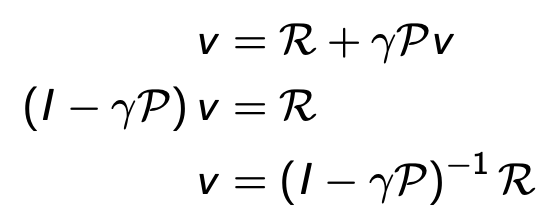
- 계산복잡도:
Markov Decision Process
Markov Decision Process

- Markov reward process with decisions
- 모든 state가 Markov한 환경
- S,A,P,R,의 tuple
- 상태전이확률, 보상이 상태와 행동에 의해 결정됨
Policy
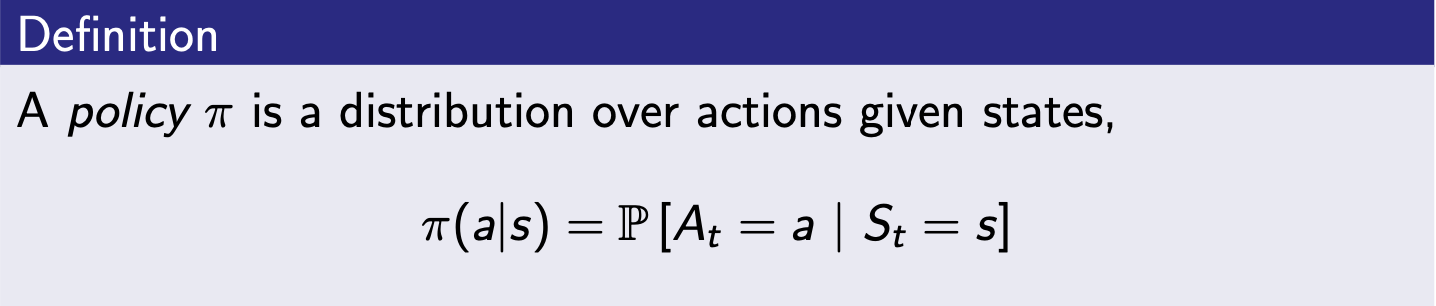
- agent의 행동을 정의
- 정책은 Markov Property --> 현재 상태에서만 의존함
- policy는 stationary
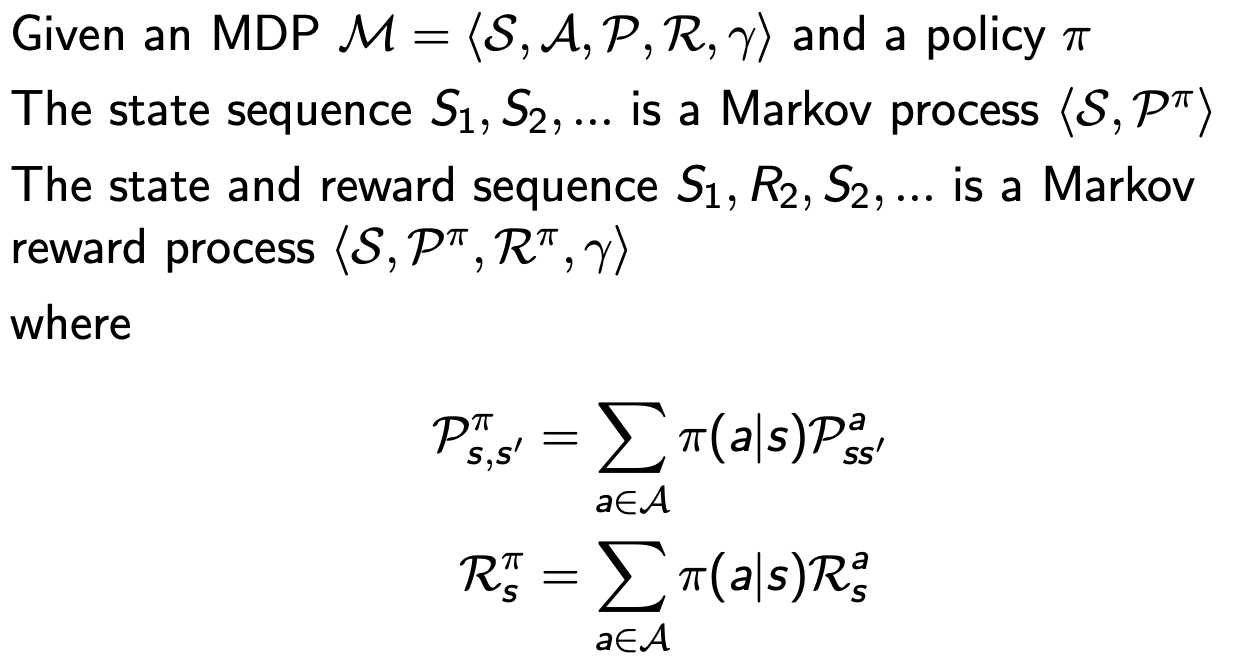
Action Value Function (행동가치함수)

- 각 행동에 대해 가치를 알려주는 함수 (Q Function = 큐함수)
--> 어떤 상태에서 어떤 행동이 얼마나 좋은지 알려주는 함수
Bellman Expectation Equation (벨만 기대 방정식)
- 특정 정책을 따라갔을 때 가치함수 사이의 관계식
상태가치함수
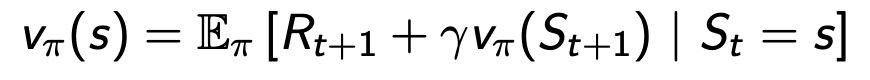
- 상태가치함수는 특정 상태의 정책 * 행동가치함수의 합으로 정의됨
- 예시
- 상태 s에서 할 수 있는 행동 2개 (검정 동그라미)
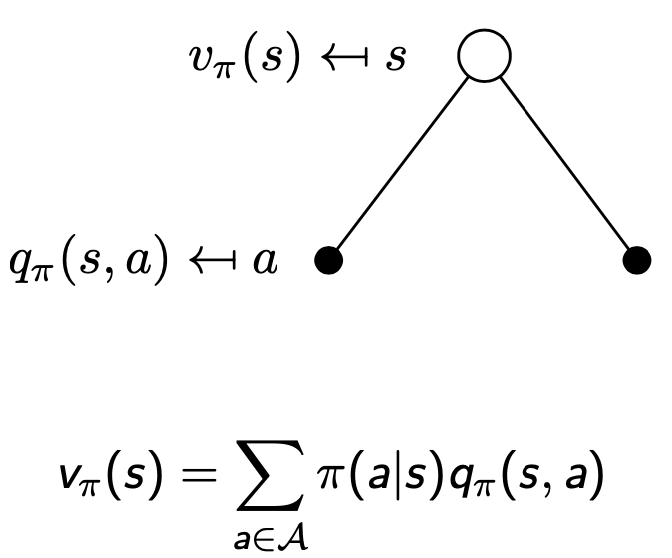
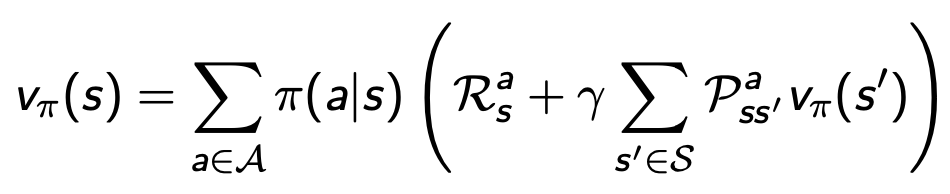
- 상태 s에서 할 수 있는 행동 2개 (검정 동그라미)
행동가치함수
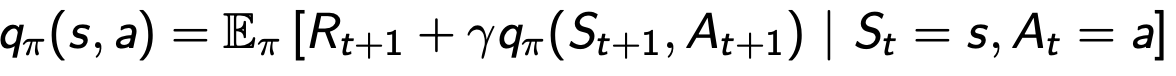
- 행동가치함수는 보상 + 할인율 (상태전이확률 다음상태가치함수의 합)으로 정의됨
- 예시
- 상태 s, 행동 a를 했을 때 발생할 수 있는 상태
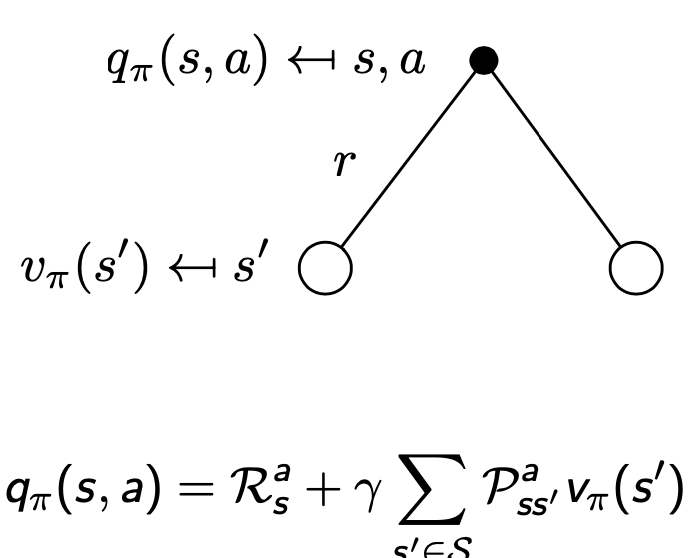
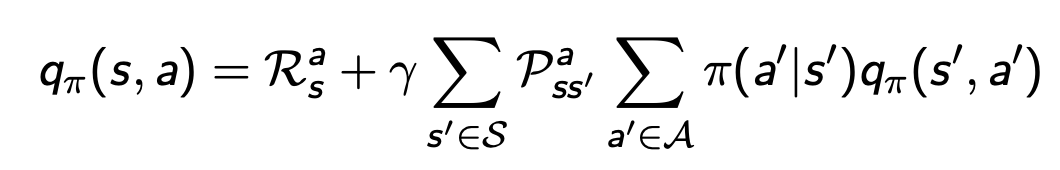
벨만기대방정식
- 예시 ()
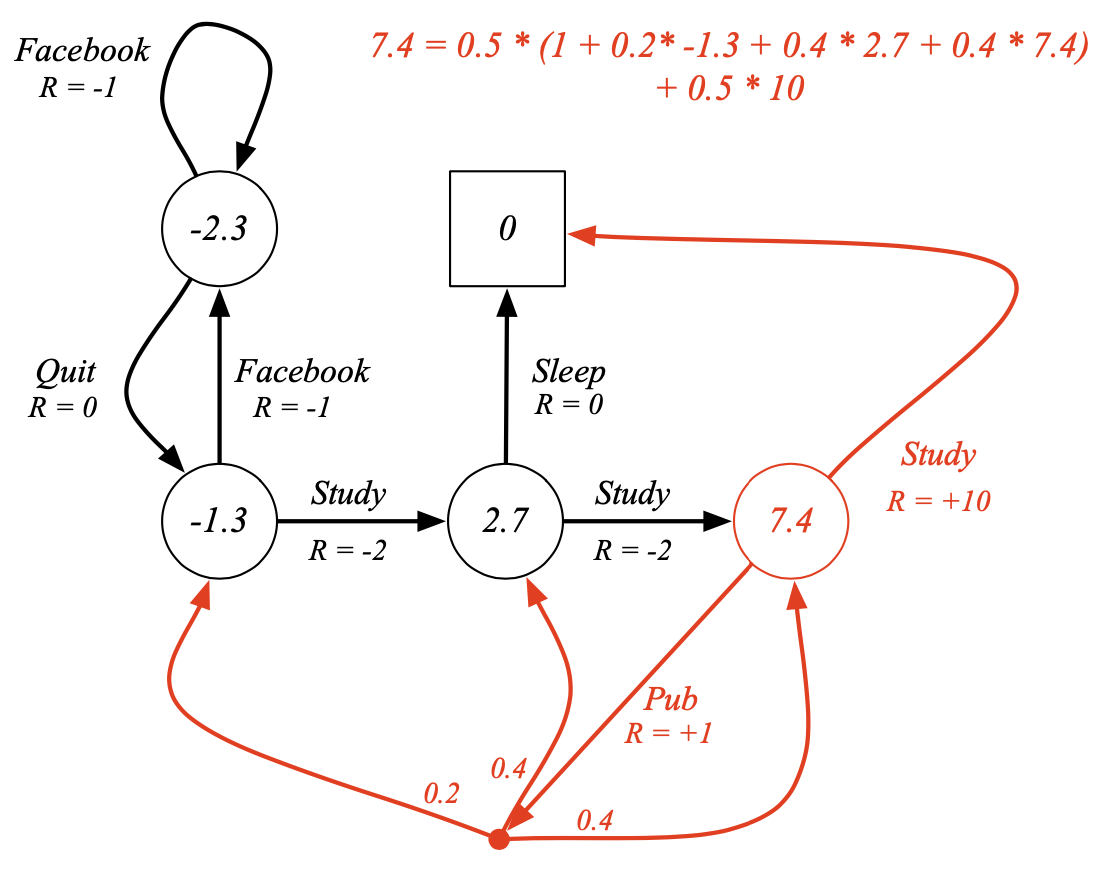
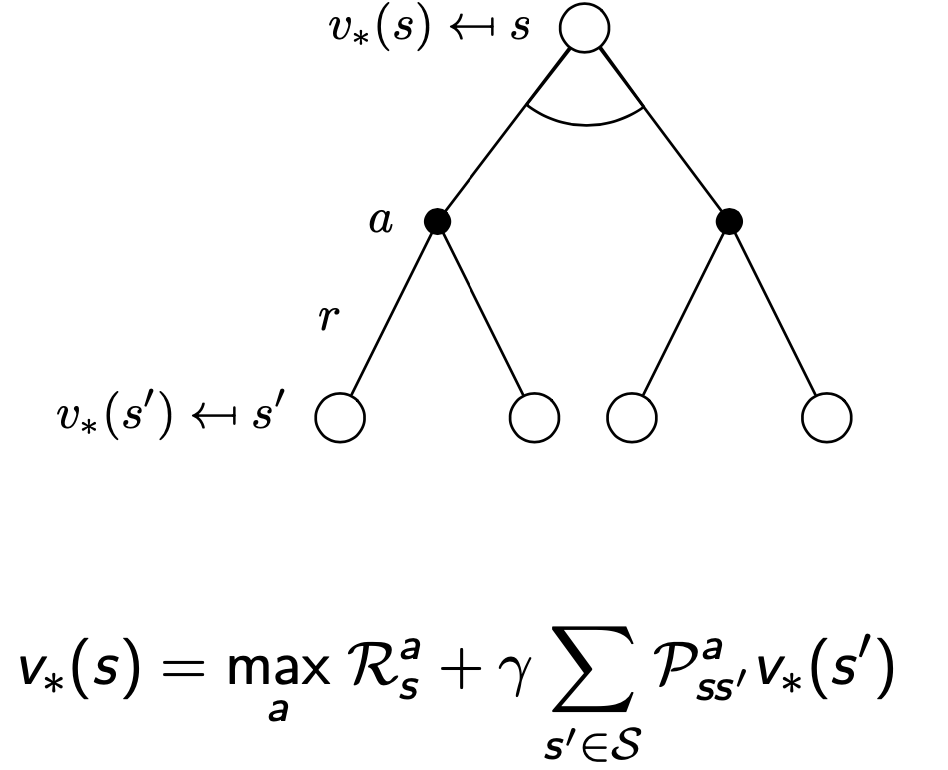
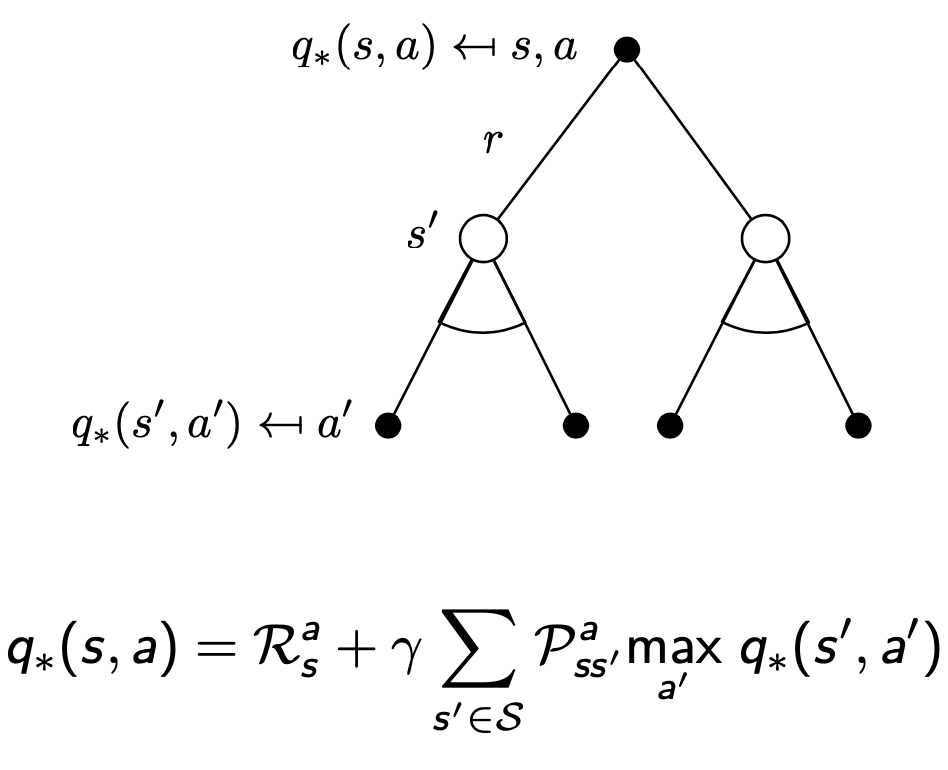
Bellman Optimality Equation (벨만 최적 방정식)

- 최적의 가치함수 사이의 관계식
- 최적 상태가치함수 : 모든 정책중 가장 큰 가치 함수
- 최적 행동가치함수 : 모든 정책중 가장 큰 행동 함수
Optimal Policy
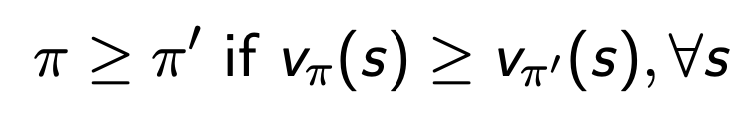
- 모든 상태에 대해서 일 때, 정책 는 정책 보다 크거나 같다.
- 최적 정책은 다른 모든 정책보다 좋거나 동등하다.

-
MDP에는 항상 deterministic optimal policy가 존재함
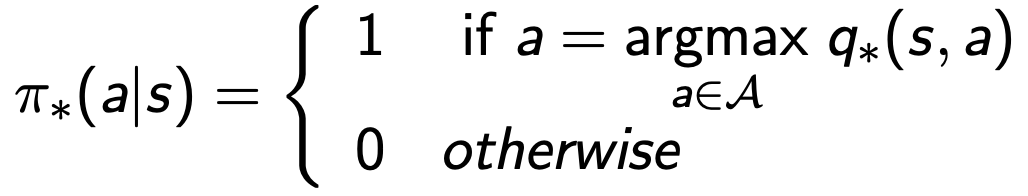
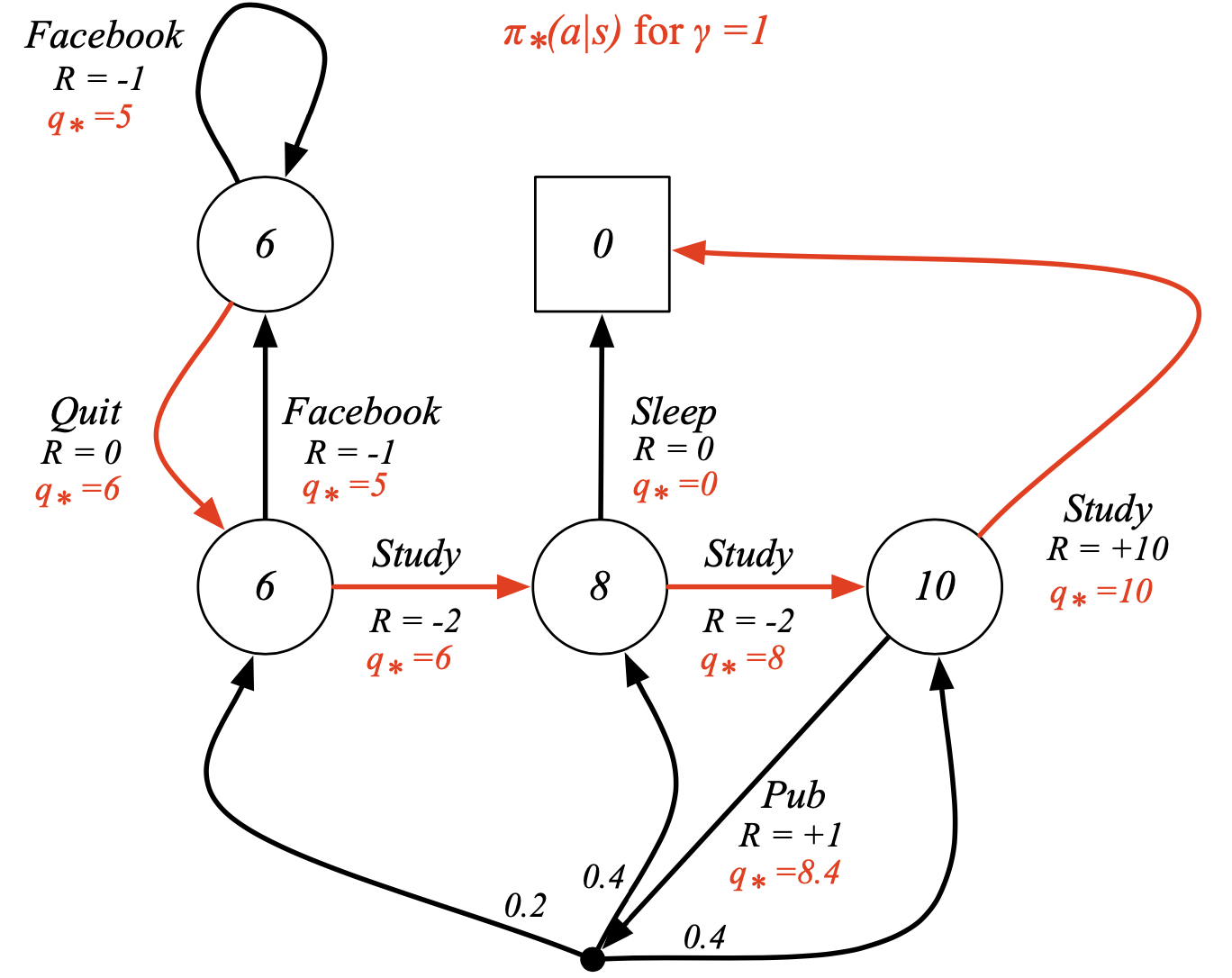
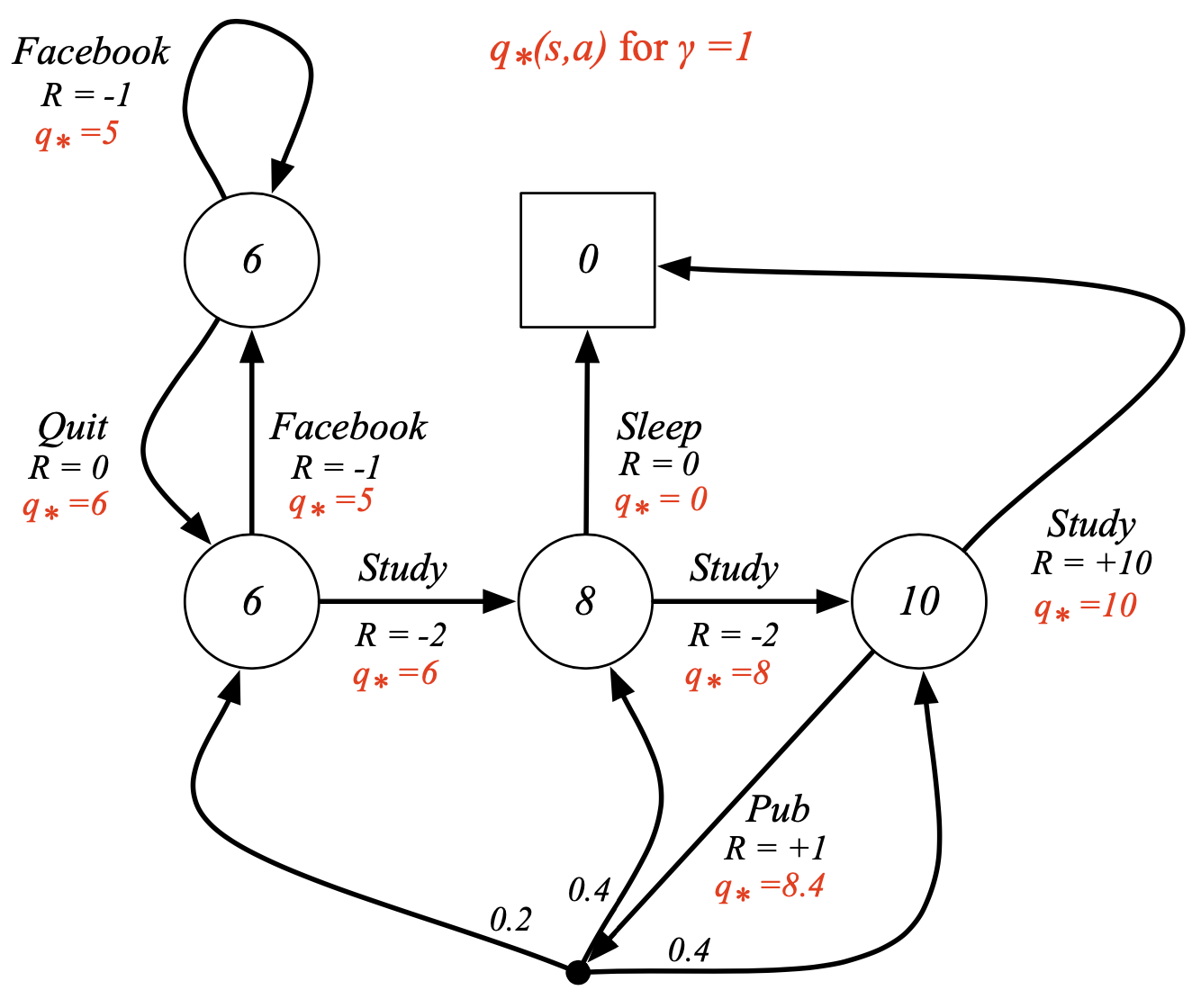
-
예시 (optimal path --> 높은 만 따라가면됨, 빨강선)