인프런 권철민님 강의 정리
Sectio5: 회귀(Regression)
개요
- 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭함

머신러닝 회귀 예측의 핵심: 주어진 피처와 결정 값 데이터 기반 학습을 통해 최적의 회귀 계수를 찾는 것
유형
- 독립변수 개수
- 단일: 독립변수가 1개인 경우
- 다중: 독립변수가 여러 개인 경우
- 회귀 계수의 결합
- 선형
- 비선형
분류, 회귀
- 분류: 결과값이 Category (Ex. 0, 1)
- 회귀: 결과값이 Continuous
종류
- 일반 선형 회귀: RSS(잔차제곱합)를 최소화할 수 있도록 회귀 계수를 최적화, 규제를 적용하지 않은 모델
- Ridge: L2 규제 적용
- Lasso: L1 규제 적용
- ElasticNet: L1, L2 규제 적용
- Logistic Regression: 분류에 사용되는 선형 모델
최적의 회귀 모델을 만든다:
1. 잔차의 합이 최소가되는 모델을 만든다!
2. 잔차의 합이 최소가 되는 최적 회귀 계수를 찾는다!
RSS
- Residual Sum of Square
- 회귀식의 w변수 (회귀 계수)가 중심 변수
- 회귀의 비용함수 (Cost Function)
- 손실함수(loss function)라고도 함
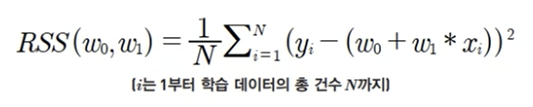
- 손실함수(loss function)라고도 함
경사하강법
- Gradient Decent
- 고차원 방정식(많은 w 파라미터가 있는 경우)에 대한 문제를 해결하면서 비용함수 RSS를 최소화하는 방법을 직관적으로 제공하는 방식
- 데이터를 기반으로 알고리즘이 스스로 학습하는 것을 가능하게 만들어준 핵심 기법
- 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식
RSS의 편미분
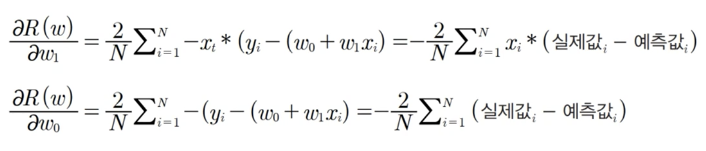
- 실제로는 편미분 값이 너무 클 수 있기 때문에 보정계수 (학습률)를 곱합
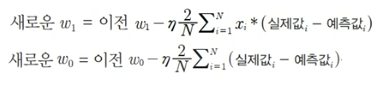
경사하강법은 새로운 w1, w0를 반복적으로 업데이트하면서 비용함수가 최소가 되는 값을 찾음
경사하강법의 프로세스

선형 회귀
다중 공선성 문제
- Multi-colinearity
- 정의: 피처간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해지는 문제
- 일반적으로 선형회귀는 입력 피처의 독립성에 많은 영향을 받음
- 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용함
회귀 평가 지표

다항 회귀
- 회귀식이 독립변수의 단항식이 아닌 2,3차 방정식과 같은 다항식으로 표현되는 것
- 원본 단항 피처들을 다항 피처들로 변환한 데이터 세트로 활용
- 사이킷런에서는 Pipeline 클래스를 이용해서 PolynomialFeatures변환과 LinearRegression 학습/예측을 결합하여 다항회귀를 구현

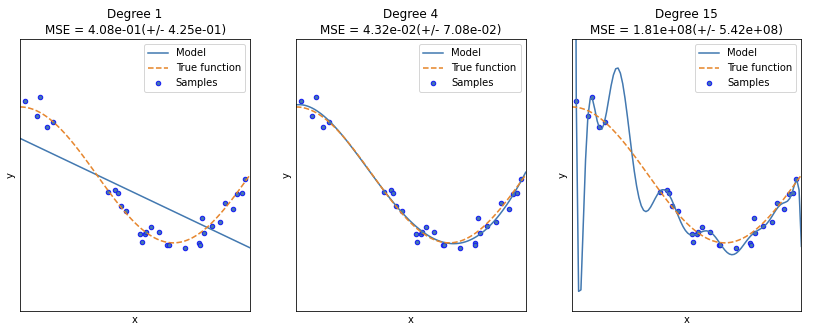
과대적합, 과소적합의 이해
- Degree1: 단순 선형 회귀로 예측 곡선이 학습 데이터의 패턴을 제대로 반영하지 못하는 과소적합 모델
- Degree4: 실제 데이터 세트와 유사한 모습
- Degree15: 예측 곡선이 학습 데이터만 정확히 예측하고 실제 테스트 데이터는 정확히 알 수 없음, 즉 학습데이터에 너무 과적합이 심한 모델이 됨
규제 선형 회귀
- 회귀 모델은 적절히 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야함

- 비용함수의 목표


유형
- L1 규제: Lasso 회귀
- 피처 선택의 특성을 가짐
- 불필요한 회귀 계수를 급격하게 감소시켜 0으로 만들고 제거함
- L2 규제: Ridge 회귀
- alpha 값이 커질수록 회귀 계수 값을 작게 만듦
- Elastic Net: L1 + L2
- L1규제가 서로 상관관계가 높은 피처들의 경우에 중요 피처만 선택하고 다른 피처들은 모두 회귀 계수를 0으로 만드는 성향을 완화하기 위해 L2 규제를 추가한 것
선형 회귀 모델을 위한 데이터 변환
- 선형 모델은 일반적으로 피처와 타겟 간에 선형 관계가 있다고 가정함
- 피처값과 타겟값의 분포가 정규분포 형태를 매우 선호함
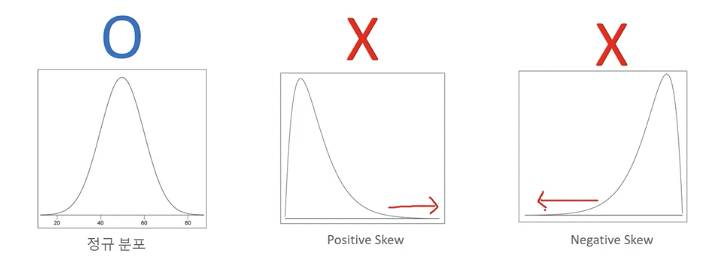
타겟값 변환
- 반드시 정규분포를 가져야함
- 주로 로그 변환을 적용함
피처값 변환
- 표준화 or 정규화를 수행함
- 다항 특성을 적용하여 변환하기도 함 (예측 성능에 향상이 없는 경우)
- 로그 변환을 적용함
- 데이터 인코딩은 원-핫 인코딩을 적용함
로지스틱 회귀
- 선형 회귀 방식을 분류에 적용한 알고리즘
- 이진분류 문제에 주로 사용됨
- 희소한 데이터 세트 분류에도 뛰어난 성능을 보임
- 선형 회귀와의 차이점은 시그모이드 함수 최적선을 찾고, 시그모이드 함수의 반환값을 확률로 간주하여 분류를 결정함
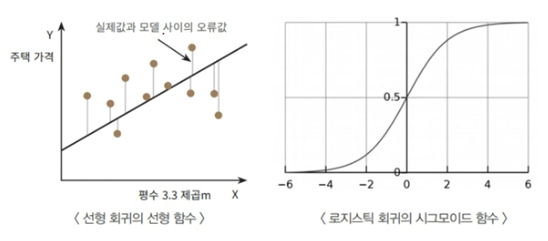
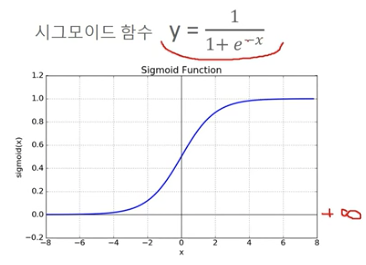
시그모이드 함수
- 0 < y < 1
오즈
- Odds(p) = p / (1-p)
- 성공확률 / 실패확률
-
--> 로지스틱 회귀는 학습을 통해 시그모이드 함수의 w를 최적화하여 예측하는 것!
회귀 트리
- CART (Classification and Regression Tree)
- 분류 뿐만 아니라 회귀도 가능한 트리 분할 알고리즘
- 분류와 유사하게 분할함, 분할 기준은 RSS(SSE)가 최소가 될 수 있는 기준
- 최종 분할이 완료된 후에는 각 분할 영역에 있는 데이터 결정값들의 평균값으로 학습/예측함