인프런 권철민님 강의 정리
Sectio6: 차원 축소(Dimension Reduction)
개요
- 차원이 커질수록 데이터 포인트들간 거리가 크게 늘어나고 데이터가 희소화 됨
- 피처가 많을 경우, 개별 피처간에 상관관계과 높아 다중 공선성 문제로 모델의 예측 성능이 저하될 수 있음
차원 축소의 장점
- 학습 시간 절약
- 모델 성능 향상
- 3차원 이하의 차원 축소의 경우 시각화를 통한 데이터 패턴 인지
피처 선택, 피처 추출
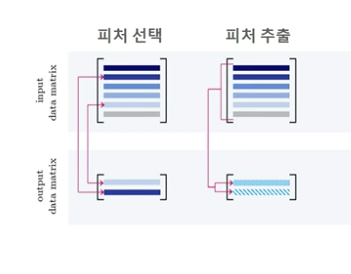
- 피처 선택: 데이터의 특징을 잘 나타내는 주요 피처만 선택
- 피처 추출: 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것, 잠재되어 있는 특성을 추출하여 나도 모르는 새로운 특성을 추출하는 것
- -예시
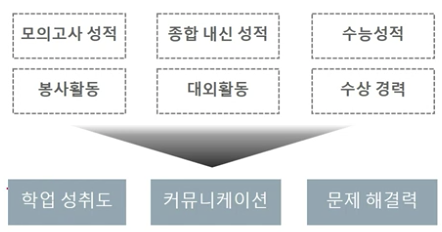
- -예시
PCA
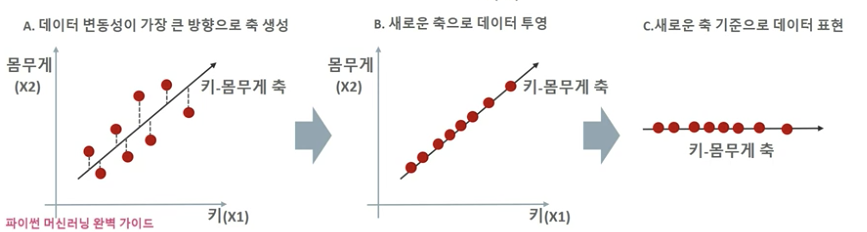
- 원본 데이터의 피처 개수에 비해 매우 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법
- 고차원의 원본 데이터를 저차원의 부분 공간으로 투영
- 원본 데이터가 가지는 데이터의 변동성을 가장 중요한 정보로 간주
PCA 변환
- Step
- 입력 데이터의 공분산 행렬 추출
- 공분산 행렬을 고유벡터와 고유값 분해
- 고유값이 가장 큰 순으로 K개 (PCA 변환 차수)만큼 고유벡터를 추출
- 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환
- 고유벡터: PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타냄
- 고유값: 고유벡터의 크기를 나타냄, 입력데이터의 분산을 나타냄
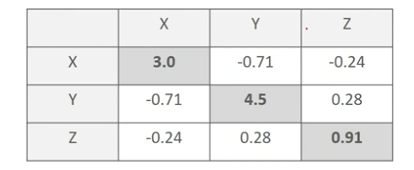
공분산 행렬
- 공분산: 두 변수 간의 변동을 의미
- Cov(X, Y) > 0 --> X가 증가할 때 Y도 증가
- 공분산 행렬은 여러 변수와 관련된 공분산을 포함하는 정방렬 행렬이며 대칭 행렬이다
선형변환, 고유벡터/고유값
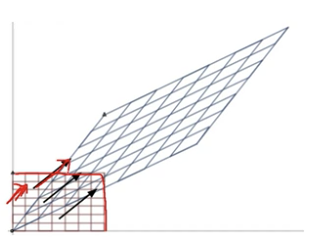
- 선형변환
- 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미
- 특정 벡터를 하나의 공간에서 다른 공간으로 투영하는 개념
- 고유벡터: 행렬 A를 곱해도 방향이 변하지 않고 크기만 변하는 벡터를 지칭
- 고유벡터는 여러 개가 존재
- 정방 행렬은 최대 그 차원 수만큼의 고유벡터를 가질 수 있음 (ex. 2*2 --> 2개)
Scikit-learn PCA
- PCA를 적용하기 전에 입력 데이터의 개별 피처들을 스케일링해야함
- 일반적으로 평균0, 분산1인 표준 정규 분포로 변환
sklearn.decomposition.PCA
LDA
- Linear Discriminant Analysis
- 선형 판별 분석법, PCA와 매우 유사
- 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소함
- PCA는 입력데이터의 변동성의 가장 큰 축을 찾았지만
- LDA는 입력데이터의 결정 값 클래스를 최대한 분리할 수 있는 축을 찾는 것
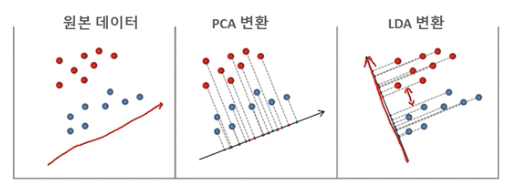
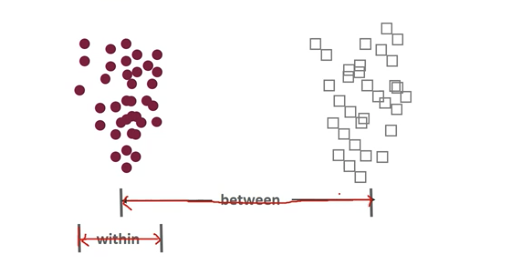
- 클래스 간 분산은 최대한 크게 가져가고, 클래스 내부의 분산은 최소한 적게 가져가는 방식
- 클래스 내부와 클래스 간 분산 행렬을 구해야함
- 클래스 내부와 클래스 간 분산 행렬을 구해야함
SVD
- Singular Value Decomposition
- 특이값 분해
고유값 분해와의 차이
- 고유값 분해
- 정방행렬만을 고유벡터로 분해함
- PCA는 분해된 고유벡터에 원본 데이터를 투영하여 차원 축소
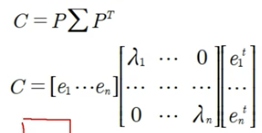
- 특이값 분해
- 행과 열이 다른 m x n 행렬도 분해 가능
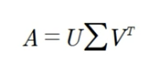
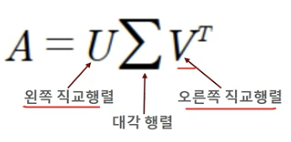
- 행과 열이 다른 m x n 행렬도 분해 가능
유형
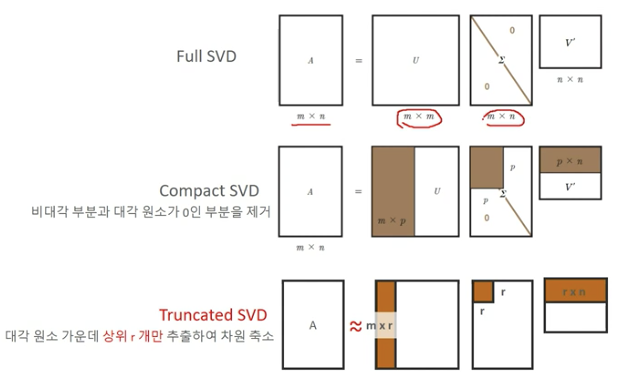
Truncated SVD 행렬 분해의 의미
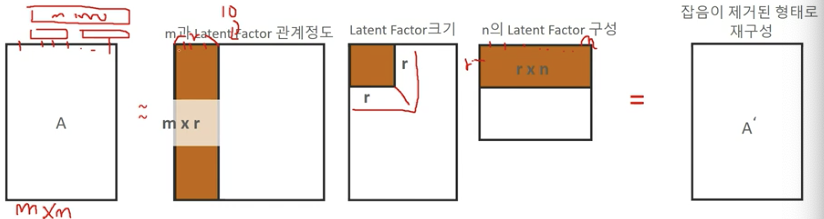
- SVD는 차원 축소를 위한 행렬분해를 통해 잠재 요인(Latent Factor)를 찾을 수 있음 (ex.추천 엔진, 문서의 잠재의미 분석)
- SVD로 차원 축소 행렬 분해된 후 다시 분해된 행렬을 애용하여 원복된 데이터 셋은 잡음(Noise)이 제거된 형태로 재구성될 수 있음
- 원본 데이터도 손실이 됨
- 원본 데이터도 손실이 됨
SVD 활용
- 이미지 압축/변환
- 추천엔진
- 문서 잠재 의미 분석
- 의사(pseudo) 역행렬을 통한 모델 예측
NMF (Non-negative Matrix Factorization)
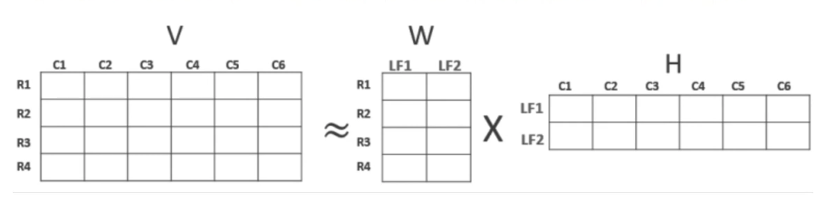
- 원본 행렬 내의 모든 원소 값이 양수라는 것이 보장 되면, 간단하게 두개의 양수 기반 행렬로 분해될 수 있는 기법
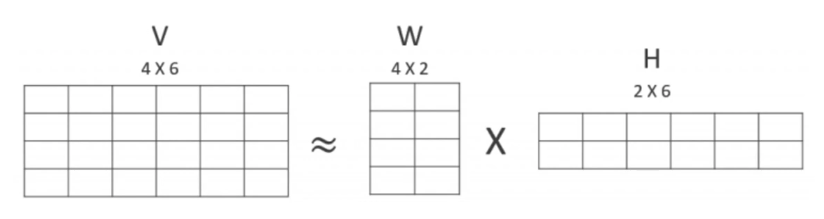
- 아래와 같이 행렬 분해를 하게 되면, W행렬과 H행렬로 구성이됨
- 분해된 행렬은 Latent Factor를 특성으로 갖게 됨
- W는 잠재 요소의 값이 얼마나 되는지에 대응하고
- H는 잠재 요소가 원본 속성에 어떻게 구성되었는지를 나타냄