인프런 권철민님 강의 정리
Sectio7: 군집화(Clustering)
군집화
- 데이터 포인트들을 별개의 군집으로 그룹화하는 것
- 유사성이 높은 데이터들을 동일한 그룹으로 분류, 서로 다른 군집들이 상이성을 갖도록 그룹화
- 활용 분야
- 고객/마켓/브랜드 세분화(segmentation)
- 이미지 검출, 트랙킹
- 이상 검출
- 알고리즘
- K-means
- Mean Shift
- Gaussian Mixture Model
- DBSCAN
K-Means Clustering
- 군집 중심점(Centroid) 기반 클러스터링
- 장점
- 일반적으로 군집화에서 가장 많이 활용됨
- 알고리즘이 쉽고 간결
- 대용량 데이터에도 활용 가능
- 단점
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우, 군집화 정확도가 떨어짐
- 몇 개의 군집을 선택할지 선택하기 어려움
- 이상치에 취약함
군집평가 - 실루엣 분석
- 각 군집 간의 거리가 얼마나 효율적으로 분리돼 있는지 나타냄
- 개별 데이터가 가지는 군집화 지표인 실루엣 계수(silhouette coefficient)를 기반으로 함
- 개별 데이터가 가지는 실루엣 계수는 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집화되어 있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리되어 있는지를 나타내는 지표
실루엣 계수
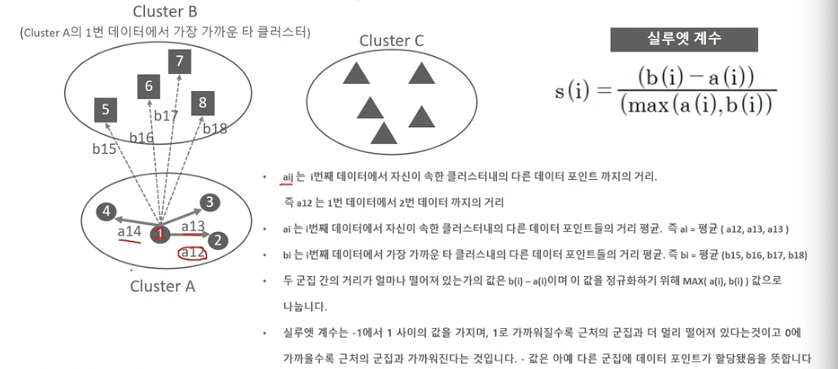
- 실루엣 계수의 평균값이 1에 가까울수록 좋음
- 전체 실루엣 계수의 평균값과 더불어 개별 군집의 평균값의 편차가 크지 않아야함
Mean Shift
- KDE를 이용하여 데이터 포인트들이 데이터 분포가 높은 곳으로 이동하면서 군집화를 수행
- 별도의 군집화 개수를 지정하지 않으며, Mean shift는 데이터 분포도에 기반하여 자동으로 군집화 개수를 정함
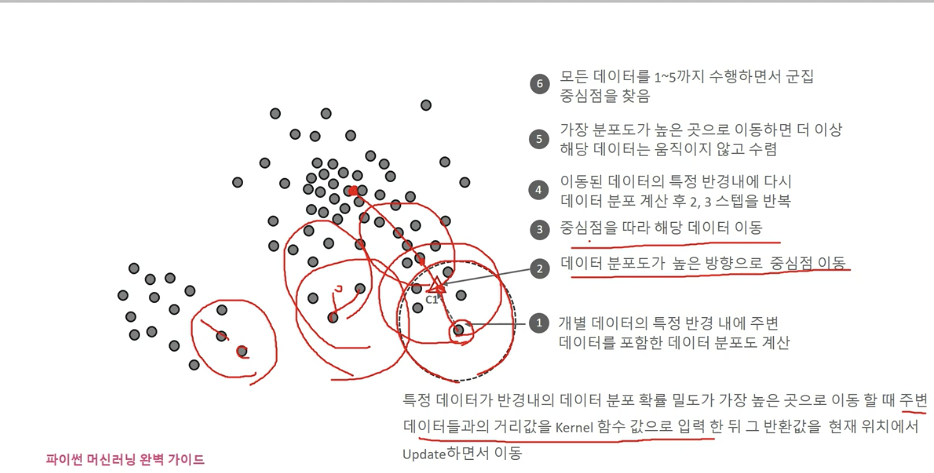
KDE (Kernel Density Estimation)
- 관측된 데이터 각각에 커널 함수를 적용한 값을 모두 더한 뒤 데이터 건수로 나누어서 확률 밀도 함수를 추정
확률 밀도 추정 방법
- 모수적 추정
- 데이터가 특정 분포를 따른다는 가정 하에서 데이터 분포를 찾는 방법
- Gaussian Mixture
- 비모수적 추정
- 데이터가 특정 분포를 따르지 않는다는 가정 하에서 밀도를 추정
- 관측된 데이터만으로 확률 밀도를 찾는 방법
- KDE
비모수적 밀도 추정 - KDE
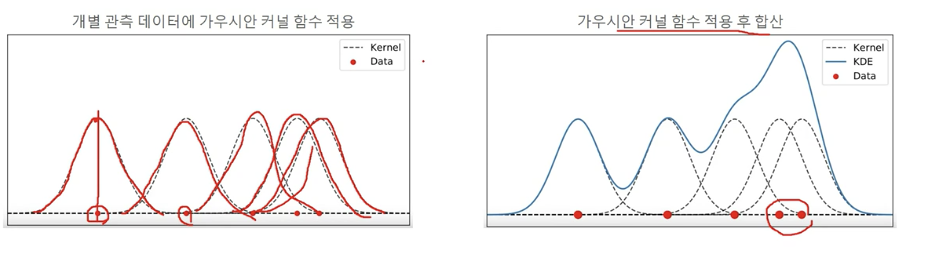
KDE와 가우시안 커널함수

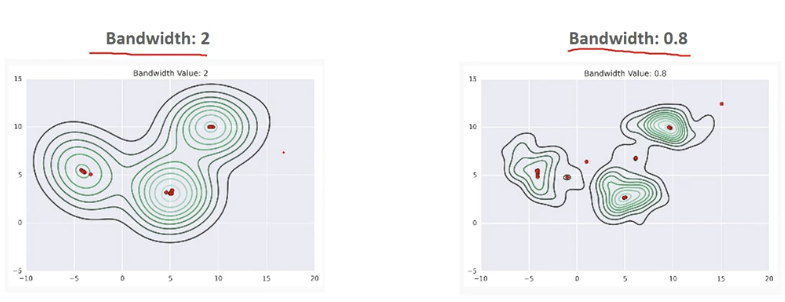
Bandwidth에 따른 KDE 변화
- Mean Shift는 Bandwidth가 클수록 적은 수의 클러스터링 중심점을, 작을수록 많은 수의 클러스터링 중심점을 가지게 됨.
- Mean Shift는 군집의 개수를 지정하지 않으며, Bandwidth의 크기에 따라 군집화를 수행
GMM
-
K-Means는 특정 중심점을 기반으로 거리적으로 퍼져있는 데이터 세트에 군집화를 적용하면 효율적
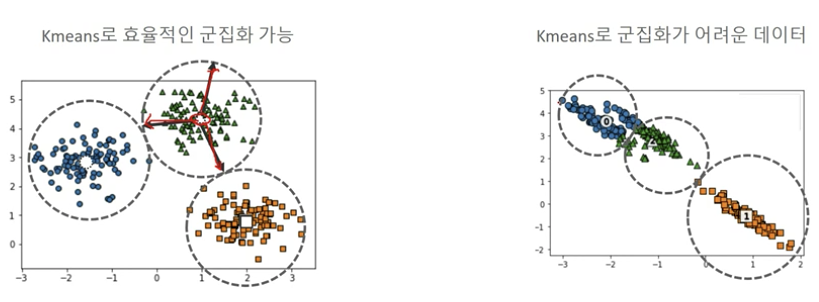
-
GMM 군집화는 군집화를 적용하고자 하는 데이터가 여러 개의 다른 가우시안 분포를 가지는 모델로 가정하고 군집화를 수행
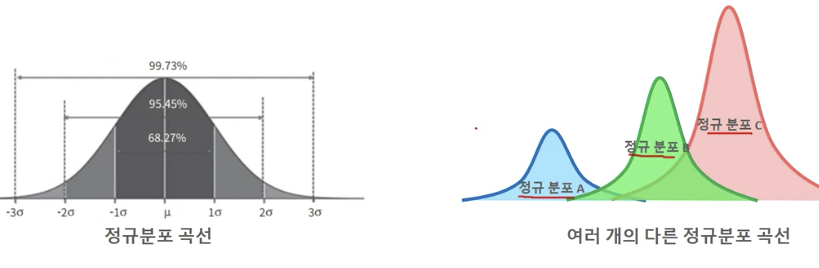
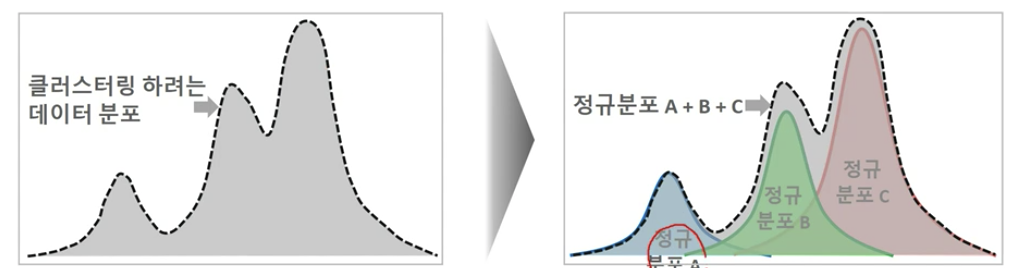
GMM 모수(Parameter) 추정
- 개별 정규 분포들의 평균과 분산, 데이터가 특정 정규 분포에 해당될 확률을 추정하는 것
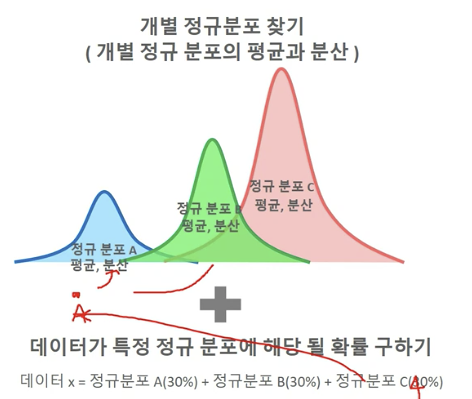
EM (Expectation and Maximization)
- Expecatation: 개별 데이터 각각에 대해서 특정 정규 분포에 소속될 확률을 구하고 가장 높은 확률을 가진 정규 분포에 소속
- Maximization: 데이터들이 특정 정규분포로 소속되면 다시 해당 정규분포의 평균과 분산을 구함
- 해당 데이터가 발견될 수 있는 가능도를 최대화 할 수 있도록 평균과 모수를 구함
- 개별 정규분포의 모수인 평균과 분산이 더 이상 변경되지 않고, 각 개별 데이터들의 정규 분포 소속이 변경되지 않으면 최종 군집화를 결정함
DBSCAN
- Density Based Spatial Clustering of Applications with Noise
- 특정 공간 내에 데이터 밀도 차이를 기반으로 하는 알고리즘
- 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행함
- 알고리즘이 데이터 밀도 차이를 자동으로 감지하여 군집을 생성하기 때문에, 사용자가 군집 개수를 지정할 수 없음
군집화 알고리즘 비교
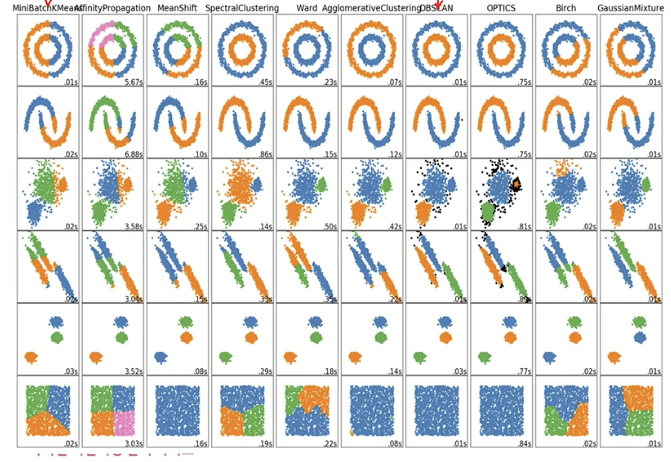
- DBSCAN은 데이터 밀도가 자주 변하거나, 모든 데이터의 밀도가 크게 변하지 않으면 군집화 성능이 떨어짐
- 피처의 개수가 많으면 군집화 성능이 떨어짐
구성 요소
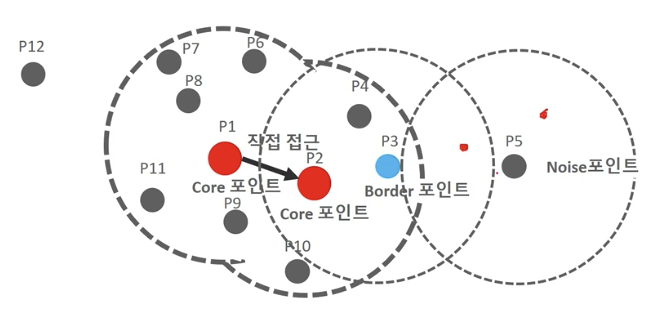
- 입실론(epsilon): 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역
- 최소 데이터 개수(min points): 개별 데이터의 입실론 주변 영역에 포함되는 타 데이터의 개수
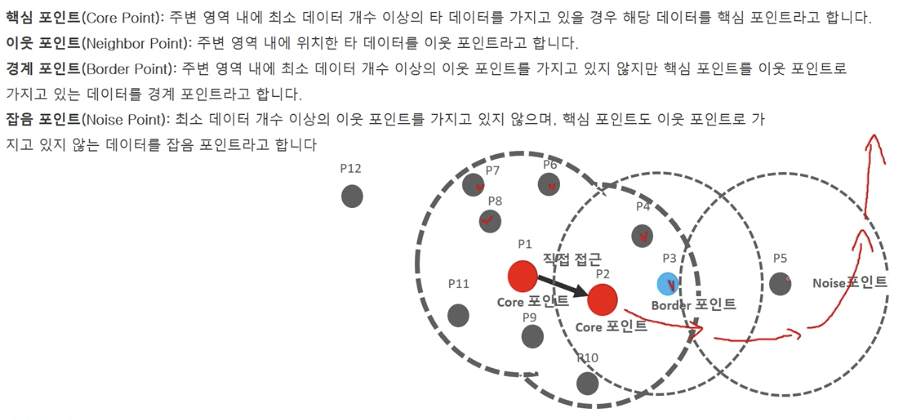
절차
-
min points 6개로 지정
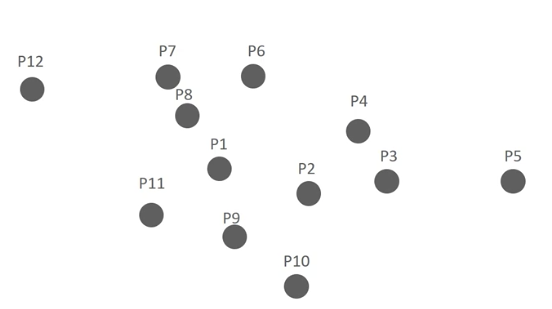
-
P1 기준, 입실론 반경 내에 포함된 데이터가 7개 임으로 Core point임
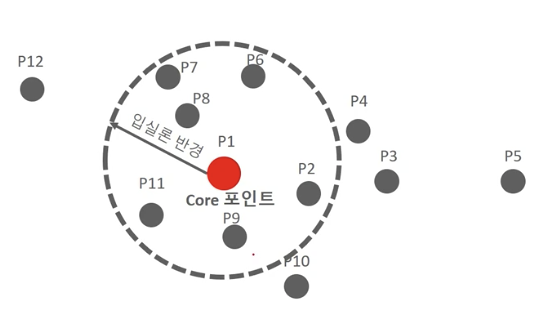
-
P2도 Core point임
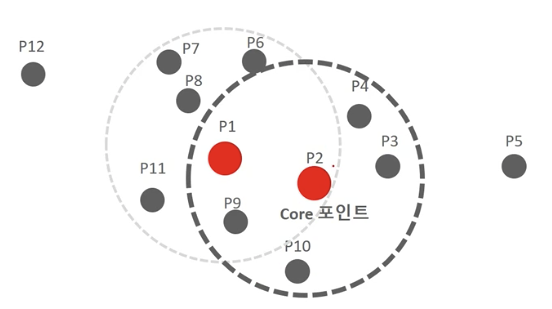
-
직접 접근이 가능한 다른 핵심 포인트를 서로 연결하면서 군집화를 구성
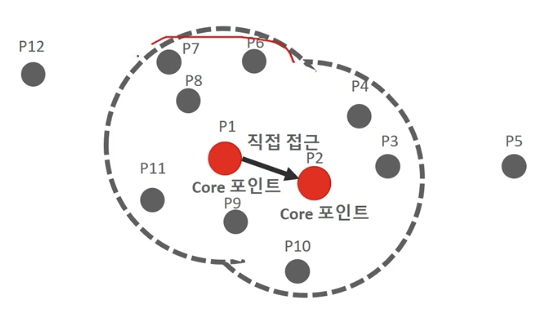
-
이웃포인트 중에 자신이 핵심포인트는 아니지만, 핵심포인트를 이웃으로 가지고 있는 경우 경계 포인트라고 함 (ex. P3). 경계 포인트는 군집의 외각을 형성
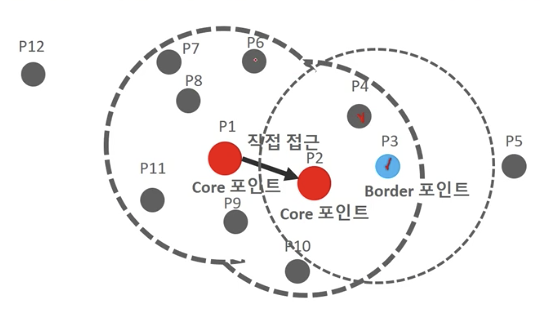
-
반경 내에 최소 데이터도 없고 핵심 포인트도 이웃으로 없는 경우 Noise point라고 함