백준 - 요세푸스 문제 2 (1168 번)

백준 - 요세푸스 문제2 (1168 번)

백준 - 요세푸스 문제1 (1158 번) 해당 문제에서 N의 크기가 늘어나고 시간제한이 줄었다.
즉, 위에서 푼 방법처럼 벡터를 Erase하면서 푸는 방식으로는 해결하지 못한다.
이는 Time Complexity를 $O(n^2)$ 밑으로 줄여야한다는 의미이다(벡터 Erase는 지운 뒤, 뒤의 원소를 한칸 씩 앞으로 당기기 때문에 $O(n^2)$의 Time Complexity를 가진다).

요세푸스 문제의 핵심은 원하는 인덱스의 숫자를 가져올 때, 삭제된 숫자들은 건너뛰어야 한다는 점이다.

예를 들어서, 0부터 시작하는 배열이 다음과 같이 있다.
Vector : 1 2 3 4
이 때 2번째 숫자인 3을 제거하고, 다시 2번째 숫자를 제거한다면 4를 제거해야 한다.
즉, 이미 지워진 숫자는 n번째 숫자를 제거하고자 배열을 탐색할 때, 카운트되면 안된다.

여기서 생각해볼 수 있는 자료구조가 Segment Tree이다.
Segment Tree는 구간합, 구간최솟값 등 특정 구간의 정보를 관리할 때 유용하게 쓰이는 자료구조이다.

본 문제에서는 Segment Tree를 다음과 같이 구간에서 살아있는 원소의 갯수를 관리하기 위해 사용한다.

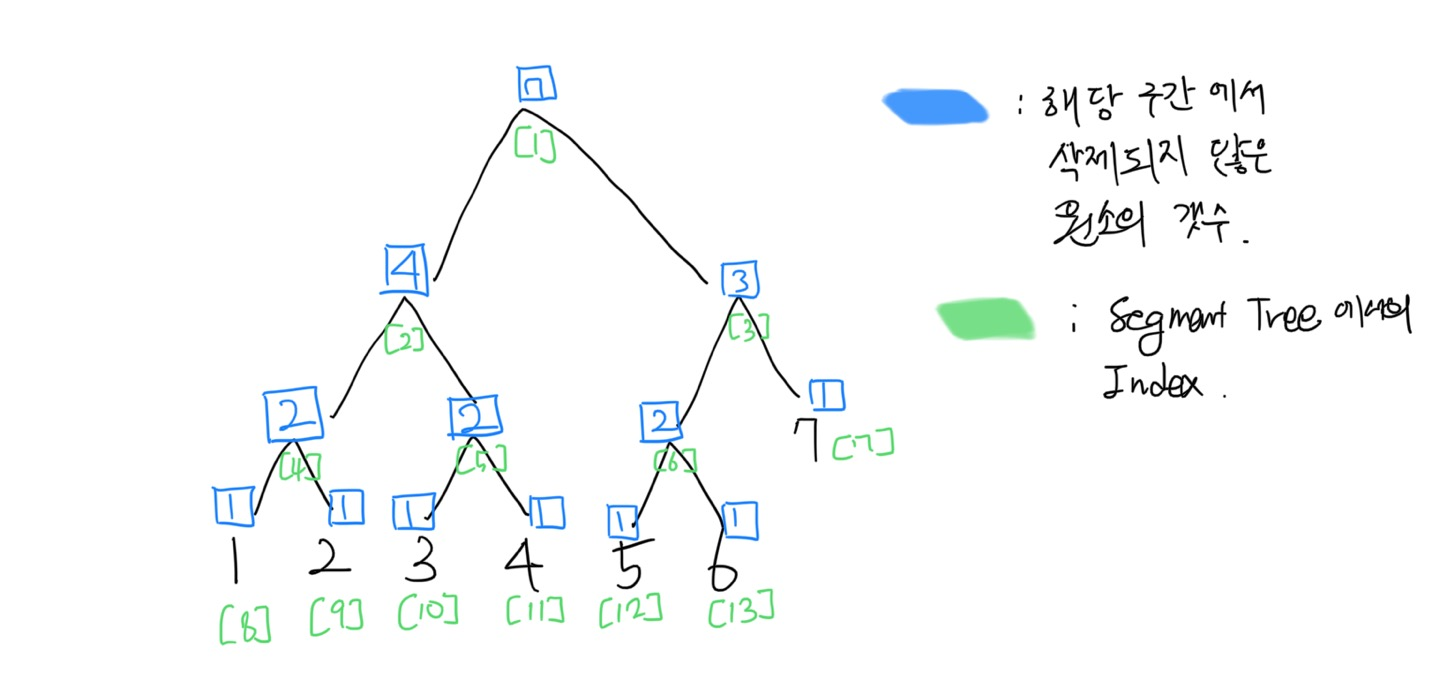
이 상태에서 3번째와 6번째가 삭제되는 과정은 다음과 같다.

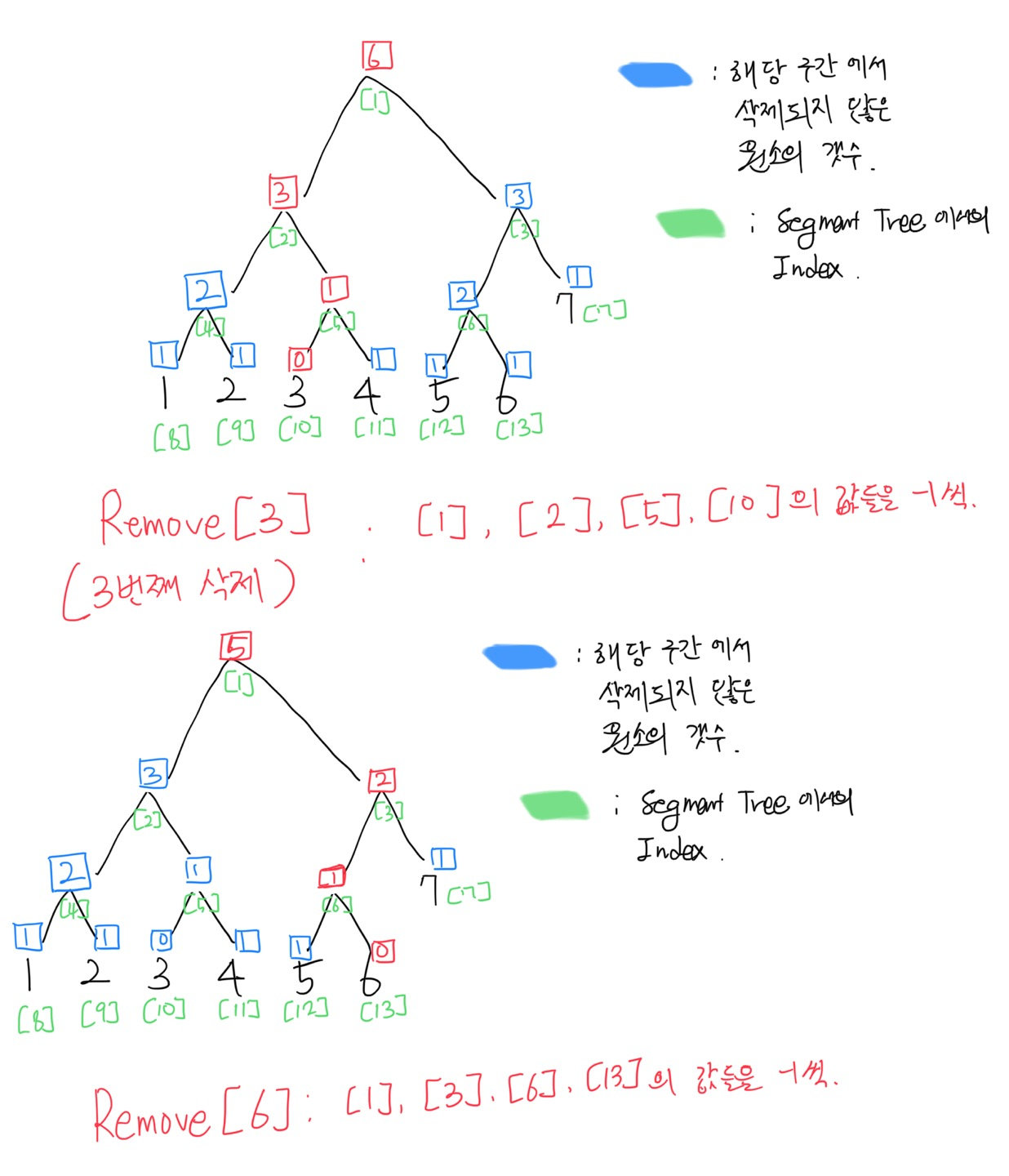
구현할 때 주의할 것은 왼쪽 노드를 삭제하는 것과 오른쪽 노드를 삭제할 때 Index를 바라보는 방식이 다르다는 것이다.

예를 들어, 첫 사진에서 5의 경우는 루트에서 오른쪽 노드로 흐르는데, 이는 1~4 다음으로 나오는 첫 번째 인덱스라는 의미이다.
이를 위해서 오른쪽으로 흐를 때에는 5를 그대로 사용하지 않고, 오른쪽으로 흐른 뒤 1번째 인덱스를 찾도록 해줘야 한다.
왼쪽으로 흐를 땐 트리를 그대로 사용해서 Index를 찾아가도 되는데, 오른쪽으로 흐를 땐 Subtree에서의 Index를 새롭게 구해야 한다고 생각하면 된다. (코드 index - segment[node * 2] 부분)

코드는 아래와 같다.

#include <iostream>

using namespace std;

int n, k;

int segment[300000];

int init(int start, int end, int node)
{
	if (start == end) 
		return segment[node] = 1;
	
	int mid = (start + end) / 2;
	return segment[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

int get_num_and_update(int start, int end, int node, int index)
{
	segment[node]--;
	if (start == end) 
		return start;
	
	int mid = (start + end) / 2;
	if (index > segment[node * 2]) 
		return get_num_and_update(mid + 1, end, node * 2 + 1, index - segment[node * 2]);
	else 
		return get_num_and_update(start, mid, node * 2, index);
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> k;

	init(1, n, 1);
	int idx = k - 1;
	cout << "<";
	for (int i = 1; i <= n; i++) {
		int get_idx = get_num_and_update(1, n, 1, idx + 1);
		
		if (i != n) 
			cout << get_idx << ", ";
		else 
			cout << get_idx;

		if (segment[1] == 0)
			break;

		idx += k - 1;
		idx %= segment[1];
	}
	cout << ">";
	return 0;
}