Vector

개발조하·2023년 11월 25일
Unity
0

Unity

목록 보기
4/30
post-thumbnail

1. Vector란?

벡터는 방향과 크기를 기술하는 중요한 수학적 개념으로, 캐릭터의 위치, 움직이는 속도, 두 객체 사이의 거리 등과 같은 속성을 기술하는 데 사용된다.

Unity에서는 2D, 3D, 4D 벡터 작업에 Vector2, Vector3, Vector4 클래스를 제공한다.
이 포스팅에서는 세 가지 유형의 벡터에 모두 적용되는 개념을 설명한다.

2. 벡터 산술에 대한 이해

2.1 덧셈

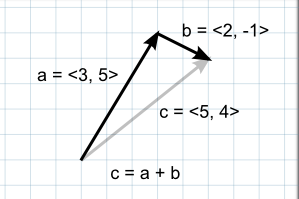
  • 위치를 나타낼 때
    첫 번째 벡터를 공간상의 점으로 간주하면, 두 번째 벡터는 그 위치에서의 offset이나 Jump로 해석할 수 있다.
    • 땅에서 위로 5 떨어진 위치 찾기
      var pointInAir = pointOnGround + new Vector2(0,5);
  • 힘을 나타낼 때
    벡터를 방향과 크기(힘의 크기)로 생각하는 것이 더 직관적이다. 두 힘 벡터를 더하면 힘의 조합에 해당하는 새로운 벡터가 생성된다. 여러 개의 별도 구성 요소가 동시에 작용하는 힘을 적용할 때 유용
    ex. 전진하는 로켓 + 측면 바람의 영향

2.2 뺄셈


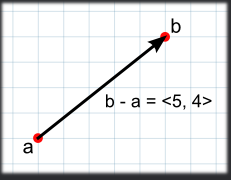
벡터의 뺄셈은 한 지점에서 다른 지점까지의 거리와 방향을 구할 때 주로 사용된다. 덧셈과 달리 벡터의 뺄셈에서는 두 파라미터의 순서가 매우 중요하다.
벡터의 음수는 원래 벡터와 동일한 크기를 갖지만, 같은 선상에서 정확히 반대 방향을 가리킨다.

2.3 오브젝트 간 방향 및 거리

공간상의 한 점을 다른 점에서 빼면, 한 객체에서 다른 객체를 향하는 벡터가 생성된다.

// 플레이어의 위치에서 목표의 위치로 향하는 벡터를 얻습니다.
var heading = target.position - player.position;
  • 벡터 정규화 (vector.Normalize() / vector.normalized)
var distance = heading.magnitude;
var direction = heading / distance; // 이제 정규화된 방향입니다.

이처럼 벡터의 크기(magnitude)로 벡터를 나누어 벡터를 수동적으로 정규화할 수 있다.
하지만 Unity에서는 Normalize() 메서드를 사용하여 다음과 같이 간소화할 수 있다. 이때도 2가지 방법이 있다.

  • 벡터를 직접 변경하여 정규화하기 (.Normalize() 메서드 호출)
Vector2 vector2 = new Vector2(x, y);
vector2.Normalize(); // 이제 vector2는 정규화됨
  • 벡터값은 그대로 유지되혹, 정규화된 복사본 만들기(.normalized 속성활용)
Vector2 normalizedVector2 = vector2.normalized; // 이것도 정규화된 벡터를 반환함
  • Player가 공중에 있는 Target에게 접근하려면? (단, Player는 지상 이동을 해야한다)

실제로 필요한 것은 플레이어의 위치에서 목표 아래 지면 바로 위의 위치로 가는 벡터이다. 뺄셈의 결과를 취하고 Y 좌표를 0으로 설정하여 이를 얻을 수 있다.

var heading = target.position - player.position;
heading.y = 0; // 이것이 지상 방향 헤딩입니다.

P는 지상 이동해야 하기 때문에 바로 T를 향해 공중을 가로질러 대각선으로 향하지 못한다.

2.4 스칼라 곱셈과 나눗셈

  • 스칼라: 숫자 하나만으로 된 데이터
    ㄴ 크기만 있고 방향은 없는 물리량 (방향성을 갖지 않는 성분, 체 집합의 원소)
    ㄴ 시간, 부피, 질량, 온도, 속력, 에너지, 전위 등

  • 벡터: 방향과 순서가 있고 차원의 공간에 존재하는 원소(숫자 여러 개가 특정한 순서대로 모여 있는 것)
    ㄴ 크기와 방향이 있는 물리량
    ㄴ 변위, 속도, 가속도, 힘, 운동량, 중력장, 자기장 등
    어떤 벡터를 자신의 크기로 나누면 그 결과는 크기가 1인 벡터가 되며, 이 벡터를 노멀라이즈 벡터라고 한다. 노멀라이즈 벡터에 스칼라를 곱하면 결과 벡터의 크기는 해당 스칼라 값과 같아진다. 힘의 방향은 일정하지만 강도를 제어할 수 있는 경우에 유용하다.

ex) 자동차 바퀴의 힘은 앞 방향으로 차를 움직이지만 그 동력은 운전자가 제어한다.

  • 힘의 방향: 자동차 바퀴가 차량을 앞으로 밀어내는 방향은 바퀴와 차량의 정렬에 따라 결정된다. 이 방향은 운전자가 핸들을 돌리지 않는 한 일정하다. 이것은 노멀라이즈된 벡터로 표현할 수 있는 방향성을 갖는다.

  • 힘의 강도 조절: 운전자가 가속 페달을 밟는 정도에 따라 엔진은 다른 양의 힘을 바퀴에 전달한다. 페달을 깊게 밟을수록 더 많은 연료가 연소되어 더 큰 힘을 발생시킨다. 이것은 노멀라이즈된 벡터에 스칼라 값을 곱하는 것과 유사하다. 여기서 스칼라 값은 페달을 밟는 정도에 해당하며, 결과적으로 차량의 속도가 증가한다.

이 예시에서, 노멀라이즈된 '벡터'는 바퀴가 차를 밀어내는 방향을 나타내고, '스칼라' 값은 가속 페달을 밟는 정도, 즉 엔진에서 발생하는 힘의 강도를 나타낸다. 이를 통해 운전자는 방향은 그대로 유지하면서 차의 속도를 조절할 수 있다.

2.5 벡터의 내적과 외적

  • 내적: 두 벡터를 결합해 하나의 숫자(스칼라)를 만드는 수학적 연산. 이 숫자는 '두 벡터가 얼마나 같은 방향을 향하고 있는지'를 나타낸다.

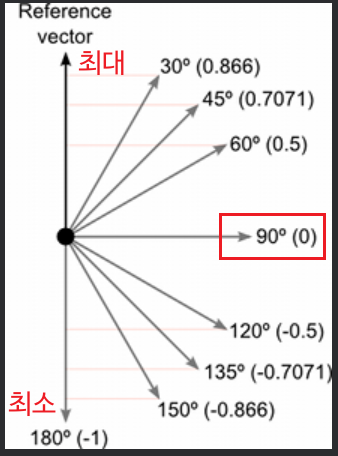화살표가 정확히 같은 방향을 가리키고 있다면, 내적 값은 최대! 반대로, 두 화살표가 서로 반대 방향을 가리키고 있다면, 내적 값은 최소! 만약 화살표들이 서로 수직(즉, 90도 각도)을 이룬다면, 내적 값은 0!

ex)
자동차의 속도계는 바퀴가 얼마나 빨리 돌아가는지를 측정한다. 하지만 자동차가 옆으로 미끄러지는 경우, 바퀴는 빠르게 돌아갈 수 있지만, 실제로 자동차는 전진하고 있지 않다. 이럴 때 내적을 사용하면, 자동차가 실제로 '앞으로' 얼마나 '빠르게' 움직이는지를 계산할 수 있다.

var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);

이 공식에서 rigidbody.velocity는 자동차가 어느 방향으로 얼마나 빠르게 움직이고 있는지를 나타내는 벡터이고, transform.forward는 자동차가 앞으로 가고 있다고 가정하는 방향의 벡터이다. 내적을 사용하여 이 두 벡터의 관계를 분석함으로써, 실제로 자동차가 앞으로 얼마나 빠르게 움직이고 있는지를 계산할 수 있다.

  • 외적: 3차원 공간에서 두 벡터(화살표)를 이용해 새로운 세 번째 벡터를 만드는 방법. 이 새로운 벡터는 처음 두 벡터와는 다른 특별한 방향을 갖는다.

당신이 공간에서 두 개의 화살표를 갖고 있을 때, 외적을 사용하면 이 두 화살표에 수직(즉, 두 화살표 모두와 직각을 이루는)인 새로운 세 번째 화살표를 만들 수 있다. 이 새 화살표의 방향을 찾는 쉬운 방법은 '오른쪽 나사 규칙'을 사용하는 것입니다.
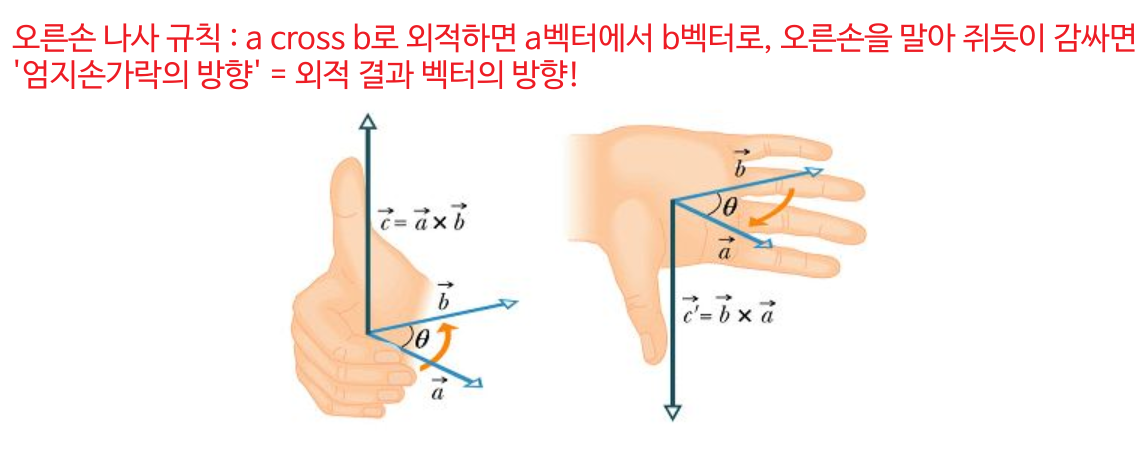이 규칙을 사용하려면, 첫 번째 화살표에서 두 번째 화살표로 손가락을 가리키며 구부리고, 엄지손가락을 편다. 엄지손가락이 가리키는 방향이 새로운 화살표의 방향이다.

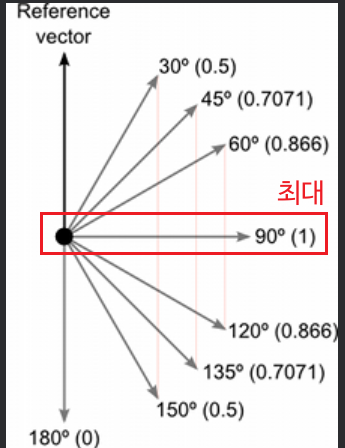
새로운 화살표의 길이(크기)는 원래 두 화살표의 크기와 그 사이의 각도에 따라 결정됩니다. 두 화살표가 서로 수직일 때, 새로운 화살표의 크기는 최대!

ex) 3D 공간
-컴퓨터 그래픽에서 물체의 표면이 어느 방향을 향하고 있는지를 결정할 때 외적을 사용할 수 있다.
-물리학에서는 물체에 작용하는 회전력(토크)의 방향을 계산할 때도 사용.

내적의 결과값은 스칼라이고, 외적의 결과값은 벡터이다.

3. Unity에서의 Vector

3.1 위치 벡터

Player의 위치를 설정해주고자 코드를 작성했다. 

struct MyVector
{
    public float x;
    public float y;
    public float z;

    public MyVector(float x, float y, float z) { this.x = x; this.y = y; this.z = z; }
}
public class PlayerController : MonoBehaviour
{
    [SerializeField] float _speed = 10.0f;

    private void Start()
    {
        MyVector position = new MyVector(0.0f, 10.0f, 0.0f);
    }
}

여기에서 Player의 위치값을 수정하고싶다면 operator로 MyVector 객체의 연산을 정의해서 사용한다. 

    public static MyVector operator +(MyVector a, MyVector b) //a벡터 + b벡터
    {
        return new MyVector(a.x + b.x, a.y + b.y, a.z + b.z);
    }
  • operator: 클래스나 구조체 내에서 특정 연산자를 오버로딩(overloading) 하기 위해 사용된다. 오버로딩이란, 기본적으로 정의된 표준연산자들(예: +, -, *, / 등)의 기능을 사용자 정의 타입(여기서는 MyVector 클래스)에 맞게 재정의하는 것이다. operator로 재정의하지 않으면 표준연산자를 직접 사용할 수 없다.
struct MyVector
{
    public float x;
    public float y;
    public float z;

    public MyVector(float x, float y, float z) { this.x = x; this.y = y; this.z = z; }
    
    public static MyVector operator +(MyVector a, MyVector b) //a벡터 + b벡터
    {
        return new MyVector(a.x + b.x, a.y + b.y, a.z + b.z);
    }
}
public class PlayerController : MonoBehaviour
{
    [SerializeField] float _speed = 10.0f;

    private void Start()
    {
        MyVector position = new MyVector(0.0f, 10.0f, 0.0f);
        position += new MyVector(0.0f, 2.0f, 0.0f);
        //position 변수의 최종 값은 MyVector(0.0f, 12.0f, 0.0f)
    }

하지만, 매번 이렇게 구조체를 선언하여 사용하는 것은 매우 귀찮은 일이다.
이에 Unity에서는 자체적으로 이러한 구조를 가진 Vector2/3/4 구조체를 제공하고 있다.
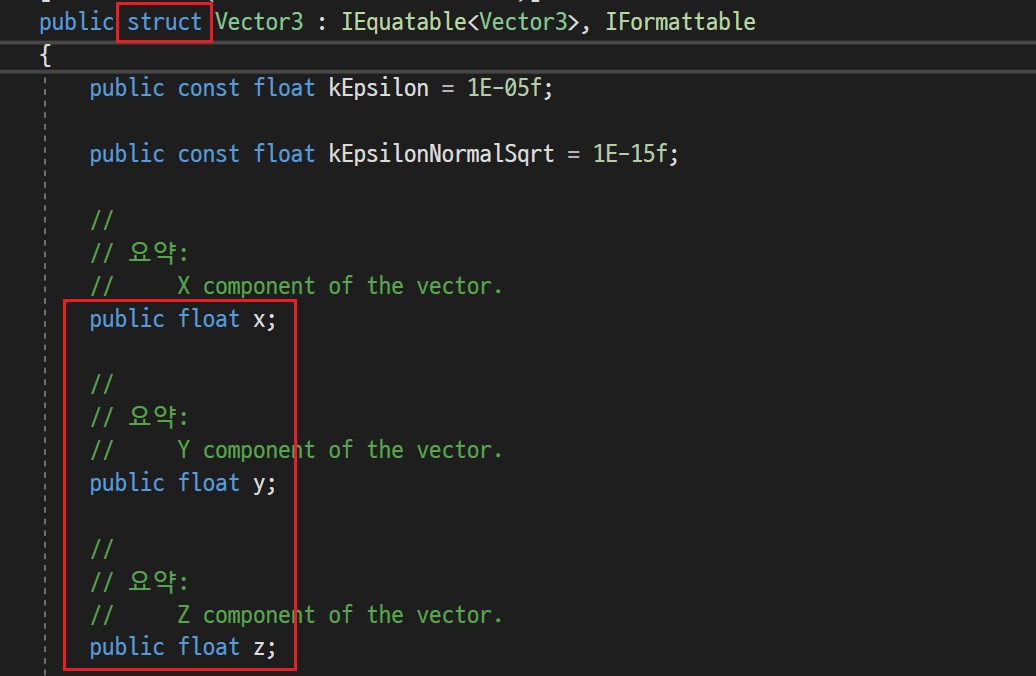
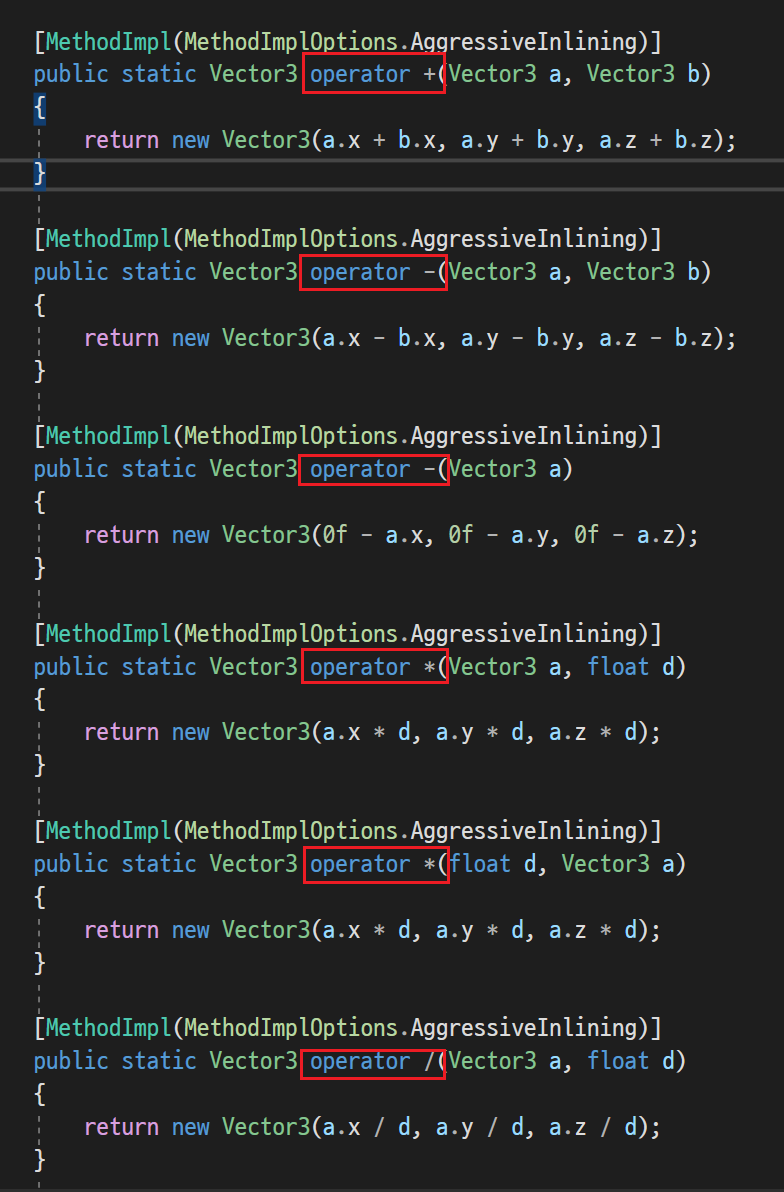ㄴ operator로 연산자 재정의도 되어있다.

이에 Player의 초기 위치값은 이렇게 작성해주면 된다.

    private void Start()
    {
         transform.position = new Vector3(0.0f, 10.0f, 0.0f);
    }

3.2 방향 벡터

위에서 작성한 MyVector 구조체를 활용하여 방향 벡터의 사용을 알아보자.

struct MyVector
{
    public float x;
    public float y;
    public float z;

    public MyVector(float x, float y, float z) { this.x = x; this.y = y; this.z = z; }
    
    public static MyVector operator +(MyVector a, MyVector b) //a벡터 + b벡터
    {
        return new MyVector(a.x + b.x, a.y + b.y, a.z + b.z);
    }
    public static MyVector operator -(MyVector a, MyVector b) //a벡터 + b벡터
    {
        return new MyVector(a.x - b.x, a.y - b.y, a.z - b.z);
    }
}
public class PlayerController : MonoBehaviour
{
    [SerializeField] float _speed = 10.0f;

    private void Start()
    {
        MyVector to = new MyVector(10.0f, 0.0f, 0.0f);
        MyVector from = new MyVector(5.0f, 0.0f, 0.0f);
        MyVector dir = to - from; //방향벡터 (5.0f, 0.0f, 0.0f)
    }
}

추가로 'operator -'도 만들어줬다.

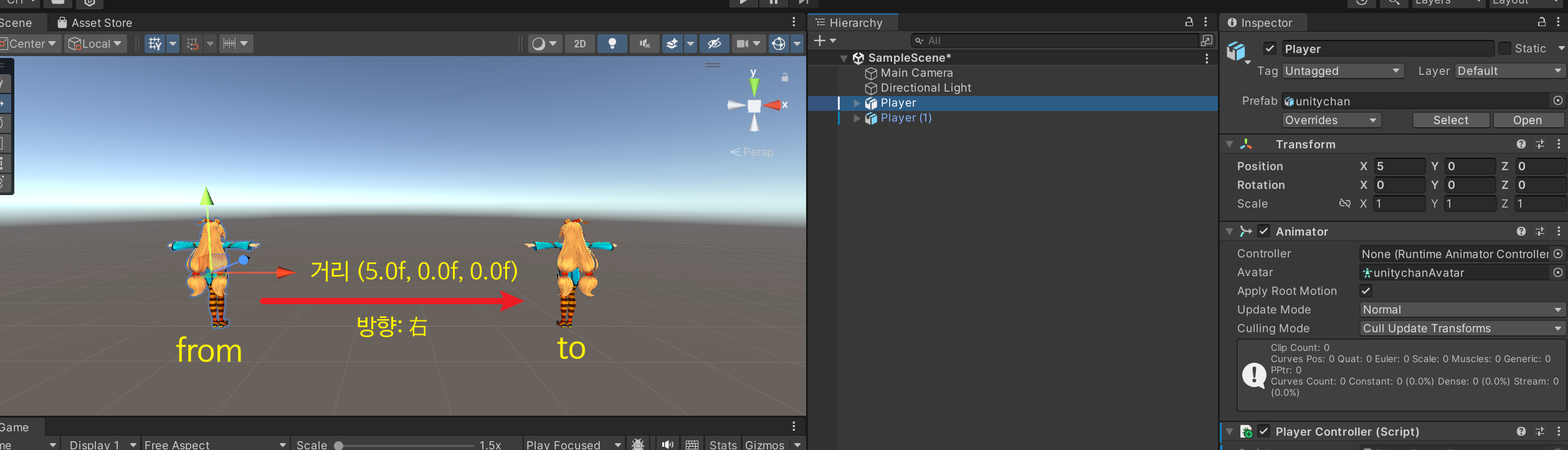
위 예시는 from좌표에 있는 캐릭터가 to좌표의 위치로 향할 때 필요한 방향 벡터를 구하고 있다.

a - b는 b에서 a로의 방향 벡터를 구하는 공식

  • 방향 벡터에서 얻을 수 있는 두 가지
    ㄴ 1. 거리(크기)
    ㄴ 2. 실제 방향
  • 벡터 크기와 방향 속성

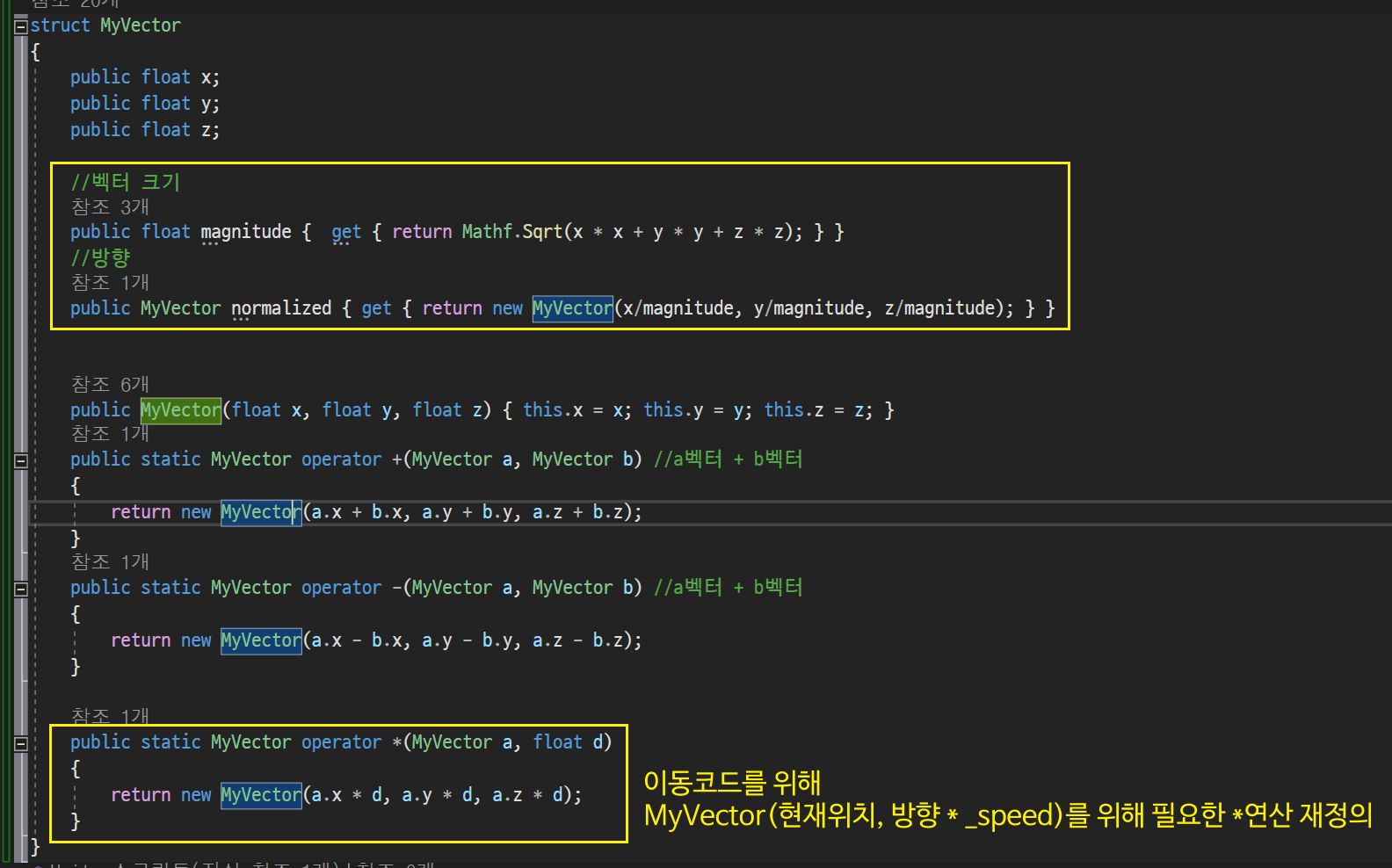
public class PlayerController : MonoBehaviour
{
    [SerializeField] float _speed = 10.0f;

    private void Start()
    {
        MyVector to = new MyVector(10.0f, 0.0f, 0.0f);
        MyVector from = new MyVector(5.0f, 0.0f, 0.0f);
        MyVector dir = to - from; //방향벡터 (5.0f, 0.0f, 0.0f)

        dir = dir.normalized; //dir은 (1.0f, 0.0f, 0.0f)가 된다

        //이동하는 코드
        MyVector newPos = from + dir * _speed; //from에서 dir방향으로 _speed로 가라
        //=> newPos는 (15.0f, 0.0f, 0.0f)이 된다.
    }
}

하지만, Unity에서는 magnitude와 normalized 역시 Vector 구조체에 정의해놨다.

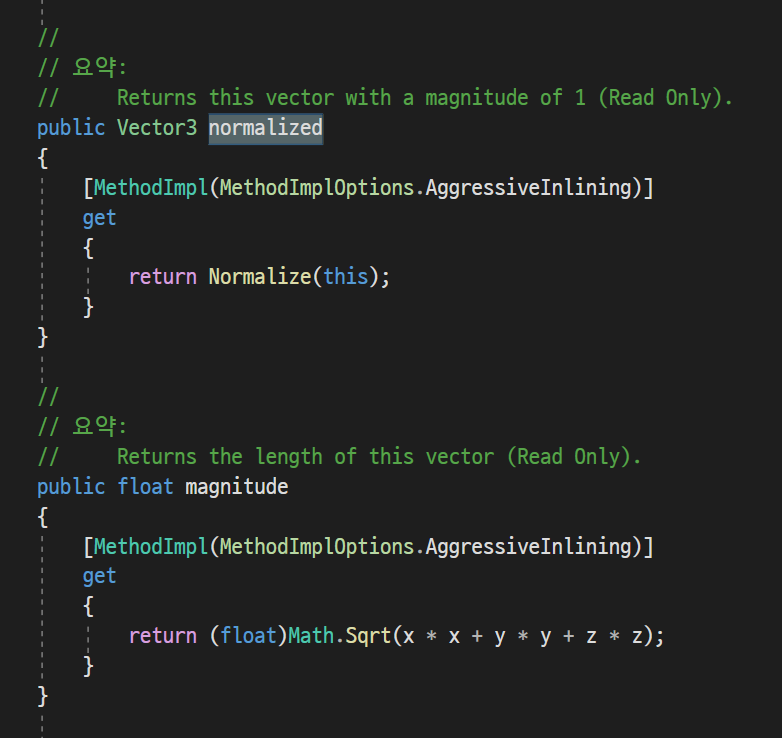
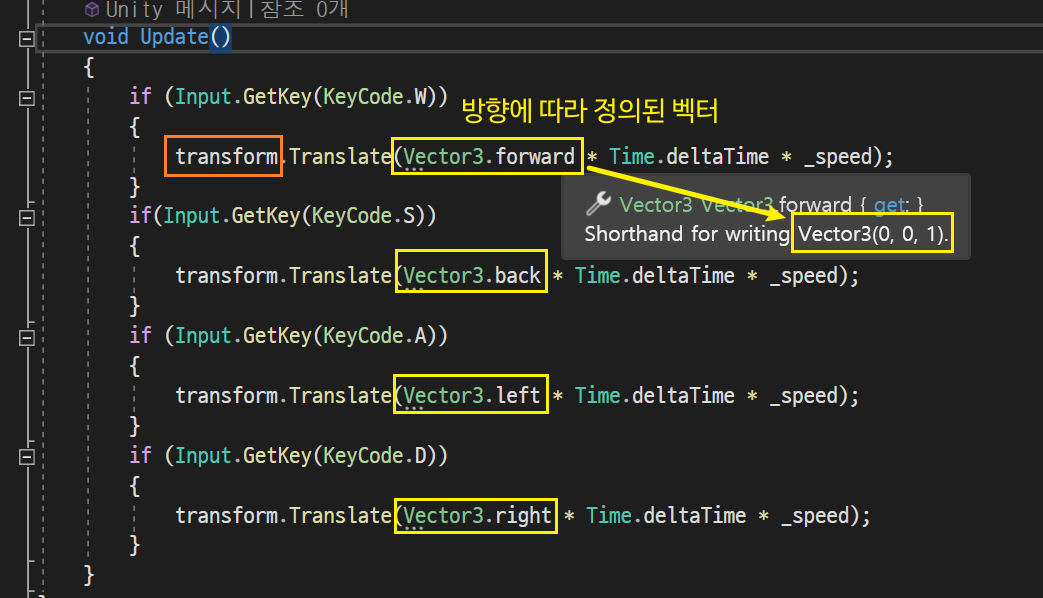
그러므로, Unity에서는 MyVector 구조체로 정의할 필요없이 Vector를 사용하여 기능을 구현할 수 있다.

📄참고자료
[인프런]c#과 유니티로 만드는 MMORPG_Vector
Vector_Unity공식 문서
벡터 vs. 스칼라
내적 vs. 외적
외적의 오른손 나사 법칙

profile
개발조하
Unity 개발자 취준생의 개발로그, Slow and steady wins the race !
이전 포스트

Transform

다음 포스트

Rotation

0개의 댓글