프로그래머스 삼각 달팽이 오답노트

삼각달팽이 문제를 풀면서 접근했던 과정들, 오류들을 기록한다.

1) 주어진 그림을 보고 어떻게 구현할 수 있을지에 대해 생각해 보았다.

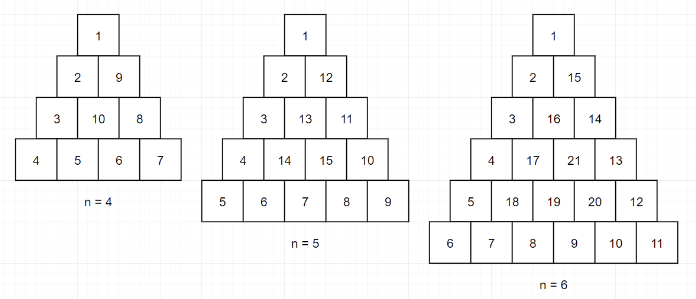
배열은 테이블 형태인데 주어진 그림은 피라미드 형태로 구성되어 있다. 이걸 배열로 변환해서 구성하려면 위치가 조정이 되어야 하고, 테두리를 따라서 반시계방향으로 회전하면서 배열에 값을 기록하려면 그 위치 조정의 패턴을 알아야 하는데 딱히 떠오르지가 않았다.

2) 그럼 수식 문제인가?

그래서 그림과 숫자를 보면서 특정 패턴을 찾아서 순서대로 값이 나오도록 해야하나? 라고 생각했는데 이마저도 쉽지 않았다. n을 늘려가면서 규칙을 찾아보기도 하고, 행마다 규칙을 찾아보기도 하고, 분할정복인가? 라고 생각해보기도 했지만 규칙이 계속 바뀌어서 궁극적으로 모든 문제를 해결할 수 있는 규칙을 찾기에는 힘들어 보였다.

3) 그래서 다시 형태를 구현하는 쪽에 무게를 두고 생각을 해보다가 스터디원이 이동을 잘 하면 된다는 힌트를 주어서 확신을 갖고 구현 방법을 생각해보았다. 그러다가 반시계 회전이 하-우-상-하-우-상 패턴으로 이루어진다는 것을 깨달았다. 그래서 이차원 리스트를 만들고 위 패턴과 이동횟수 규칙을 찾아 이동하면서 리스트에 저장하자.라고 생각하고 구현을 했다. N이 4일 때 하:4 , 우:3, 상:2 ...개씩 값을 저장하고 방향을 바꿨다. 구현을 끝내보니 내 방식은 이동하면서 이차원 리스트에 값을 저장하므로 예시 그림처럼 3, 10, 8 의 순서가 보장되지 않고, 먼저 이동한 곳부터 리스트에 넣어 3, 8, 10이 출력되는 것을 알았다. 정확하게 알고리즘이 주어진 TC를 출력하는 지에 대해 검증 없이 시작했다가 시간을 날려버리게 되었다.

4) 그래서 결국 시간 내에 문제를 해결하지 못 하고 답을 확인했다. 스터디 원의 공유를 통해 배열을 만들고 직각삼각형 형태로 배열에 값을 저장하면 된다는 것을 깨달았다.

이 형태로 이동하면서 값을 저장하면 배열 공간으로 순서를 보장하면서 값을 저장할 수 있다. 결국 그림의 피라미드를 좌로 정렬해서 보면 이동하는 아이디어를 쉽게 얻을 수 있었을 텐데 그 생각을 하지 못 하고 그림에 갇혀서 생각했다.

이 생각만 한다면 쉽게 아래와 같이 풀 수 있다.

import java.util.*;

class Solution {
    public int[] solution(int n) {
                
        int[] answer = new int[n*(n+1)/2];
        int[] dr = {1,0,-1};
        int[] dc = {0,1,-1};
        int[][] arr = new int[n][n];
        
        int num = 1;
        int d = 0;
        int r = -1;
        int c = 0;
     
        for(int i=0; i<n; i++){
            d = i % 3;
            for(int j=i; j<n; j++){
                r = r + dr[d];
                c = c + dc[d];
                arr[r][c] = num++;
            }
        }
        
        int idx = 0;
        for(int i=0; i<n; i++){
            for(int j=0; j<=i; j++){
                answer[idx++] = arr[i][j];
            }
        }
        return answer;
    }
}