트라이
트라이는 문자열 집합을 관리하는 트리입니다.
간선마다 알파벳 하나가 대응되고, 자식 노드와 연결된 간선 중 어떤 알파벳과 대응되는 간선은 최대 하나입니다.
트리를 내려가면서 만나는 간선의 알파벳을 모두 이으면 원래 문자열을 얻을 수 있고, 두 문자열의 접두사가 같다면 그 길이만큼의 간선을 트리에서 공유합니다.
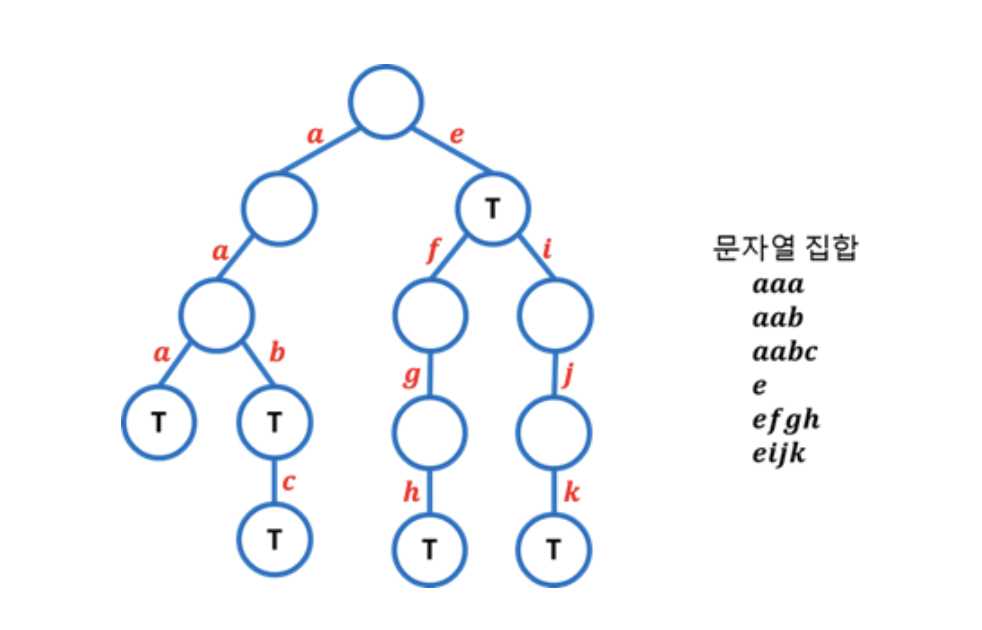
T는 문자열의 끝이라는 표시입니다. 루트 노드에서 T 노드로 가는 경로의 알파벳을 이으면 집합에 포함된 문자열을 얻을 수 있습니다.
만약 이러한 표시가 없다면 트라이에서 원래 문자열 집합을 전부 뽑아낼 수 없습니다.
노드
struct TrieNode {
bool is_terminal;
// std::map< char, TrieNode*> child; // 첫 번째 방법
// TrieNode* child[CHAR_NUM]; // 두 번째 방법
};문자열의 끝을 표시하는 Boolean 변수를 두었습니다. True / False 대신 개수를 표기하여 원소의 중복을 허용하는 트라이를 만들 수도 있습니다.
간선을 저장하는 데 두 가지 방법이 있습니다. 첫 번째는 std::map에 사용하는 간선만큼의 데이터만 저장하는 방법이고, 두 번째 방법은 사용되는 문자 종류의 개수만큼 간선을 만들어서 배열에 저장하는 방법입니다.
첫 번째 방법은 불필요한 간선을 만들지 않지만 std::map 자체가 많이 무겁습니다. 만약 사용되는 문자의 종류가 적다면(이를 테면 문자열이 알파벳 소문자로만 되어 있을 경우) 두 번째 방법이 더 효과적입니다.
트리 내려가기
트라이의 루트 노드부터 내려가는 코드는 아래처럼 생겼습니다.
std::string str;
TrieNode* n = root_node;
for (const char& c : str) {
if (n->child[c] == nullptr) {
n->child[c] = new_node();
}
n = n->child[c];
}루트 노드에서 시작하여, 문자열의 문자를 하나씩 보면서 해당하는 간선으로 이동합니다. 만약 간선 너머가 NULL이라면, 즉석에서 새 노드를 만들어서 붙여줍니다.
트라이에서의 삽입/삭제/탐색 모두 위의 방식을 기본으로 합니다.
구현
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
class Trie {
const static int M = 26;
const static char OFFSET = 'a';
struct TrieNode {
int child[M];
bool is_terminal;
TrieNode() {
memset(child, -1, sizeof(int) * M);
is_terminal = false;
}
};
vector<TrieNode> nodes;
public:
Trie() : nodes(1) {}
void init() {
nodes.resize(1);
nodes[0] = TrieNode();
}
void insert(const string& str) {
int node_id = 0;
for (const char c : str) {
if (nodes[node_id].child[c - OFFSET] == -1) {
nodes[node_id].child[c - OFFSET] = nodes.size();
nodes.__emplace_back(TrieNode());
}
node_id = nodes[node_id].child[c - OFFSET];
}
nodes[node_id].is_terminal = true;
}
void remove(const string& str) {
int node_id = 0;
for (const char c : str) {
if (nodes[node_id].child[c - OFFSET] == -1) {
return;
}
node_id = nodes[node_id].child[c - OFFSET];
}
nodes[node_id].is_terminal = false;
}
bool find(const string& str) const {
int node_id = 0;
for (const char c : str) {
if (nodes[node_id].child[c - OFFSET] == -1) {
return false;
}
node_id = nodes[node_id].child[c - OFFSET];
}
return nodes[node_id].is_terminal;
}
};
int main(void){
Trie trie = Trie();
trie.insert("apple");
cout << trie.find("apple") << endl; // 1
trie.remove("apple");
cout << trie.find("apple") << endl; // 0
return 0;
}2.5. 활용
트라이에서 문자열의 삽입/삭제/탐색은 언제나 O(문자열의 길이)입니다. 이는 해시와 같은 시간 복잡도로 매우 빠릅니다.
해시는 데이터 순서를 무작위로 저장하지만, 트라이는 다릅니다. 트라이도 트리의 한 종류이기 때문에 Binary Search Tree의 동작을 응용하여 k번째 문자열 찾기, 같은 접두사를 가지는 문자열 개수 세기 등 해시 테이블로는 할 수 없는 동작까지 할 수 있습니다.
