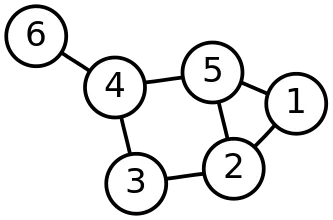
그래프의 정의
-
정점(Vertax)의 모음과 간선(Edge)의 모음의 결합
-
정점의 집합을 V, 간선의 집합을 E라고 했을때 그래프 G = (V, E)
-
인접(Adjacent): 간선으로 연결된 두 정점
-
경로(Path): 정점들 끼리의 길 ex) A-B-C
-
경로의 길이: 정점과 정점 사이에 있는 간선의 수
-
사이클(Cycle): 어느 경로가 한 정점을 두번이상 거치는 경우 -> 트리에서는 볼 수 없는 특징
-
방향성
방향성 그래프(Directed Graph)
무방향성 그래프(Undirected Graph) -
연결성(Connectivity):
무방향성 그래프에서 두 정점 사이에 경로가 존재하면 두 정점은 연결되어있다.
그래프내의 각 정점이 다른 모든 정점과 연결되어 있다면 이 그래프는 연결되어있다.
그래프의 표현방법
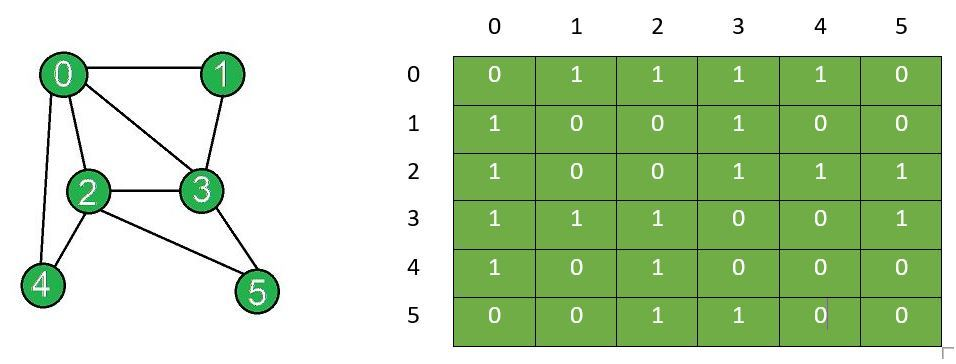
인접 행렬(Adjacency Matrix)
https://www.geeksforgeeks.org/add-and-remove-edge-in-adjacency-matrix-representation-of-a-graph/
- 정점끼리 인접관계를 나타내는 행렬
- 장점: 정점간의 인접 여부를 배열 index를 이용해 빠르게 알 수 있다.
- 단점: 사용하는 메모리 양이 정점의 크기*N^2만큼 커짐
인접 리스트(Adjacency List)
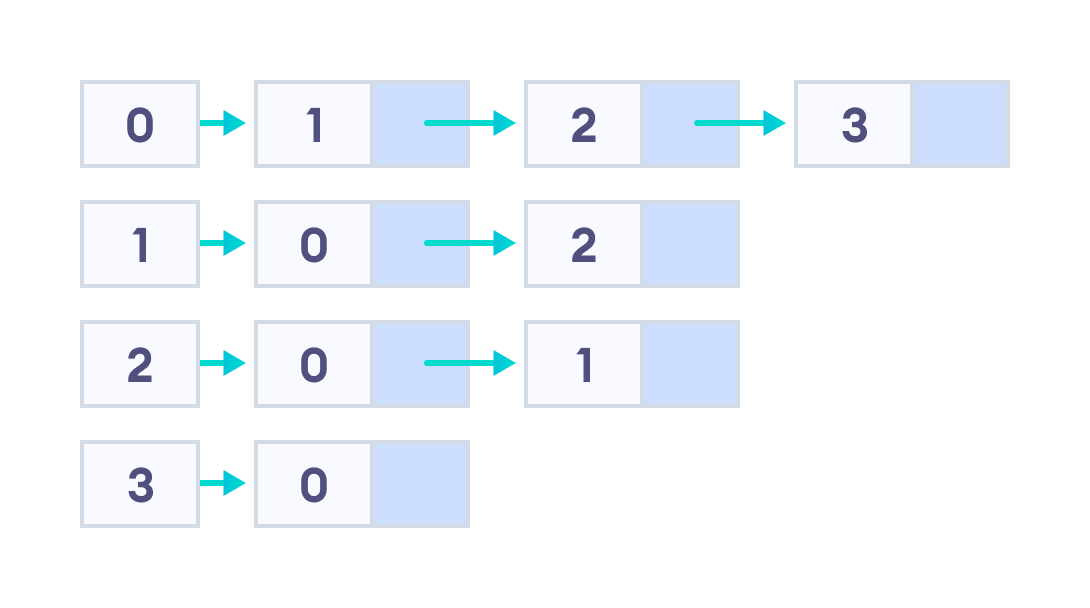
- 각 정점이 자신과 인접한 모든 정점의 목록을 리스트로 관리하도록 하는 기법
- 장점: 정점과 간선의 삽입이 빠르고 사용하는 메모리양이 적다.
- 단점: 인접 리스트를 타고 순차탐색 해야함.
그래프 순회 기법
깊이 우선 탐색(Depth First Search)
- 더 나아갈 길이 보이지 않을 때까지 깊이 들어간다.
- 시작정점을 정하고
방문했음으로 정한다. - 시작정점의 이웃정점을 새로운 시작 정점으로 정하고 DFS 다시 수행
- 더 이상 방문하지 않은 인접 정점이 없다면 이전정점으로 돌아가서 DFS수행
- 이전정점으로 끝까지 돌아가도 방문하지 않은 이웃 정점이 없다면 모두 탐색 완료
- 재귀(또는 스택)을 이용하여 구현
void DFS(Vertex* V) // 깊이 우선 탐색
{
Edge* adjList = V->AdjacencyList; // 매개변수로 받은 정점의 인접 정점 리스트
printf("%d ", V->Data);
V->Visited = Visited; // 매개변수로 받은 정점 방문
while (adjList != NULL)
{
if (adjList->Target != NULL && adjList->Target->Visited == NotVisited)
{
DFS(adjList->Target); // 재귀를 이용
}
adjList = adjList->Next; // 다음 인접정점으로
}
}너비 우선 탐색(Breadth First Search)
- 꼼꼼하게 좌우를 살피며 다니자
- 시작정점을 방문으로 표시하고 큐에 집어 넣는다
- 큐에서 dequeue한 정점의 인접정점중 방문하지 않은 정점들을 방문으로 표시하고 모두 큐에 넣는다.
- 큐가 빌때까지 2. 를 반복
- 큐를 이용하여 구현
void BFS( Vertex* V, LinkedQueue* Queue )
{
// 시작 정점 큐에 넣기
V->Visited = Visited;
printf("%d ", V->Data);
LQ_Enqueue(Queue, LQ_CreateNode(V));
// 시작 정점에 대해한 작업 끝
Edge* E = NULL;
while (!LQ_IsEmpty(Queue)) // 큐가 빌때까지
{
V = LQ_Dequeue(Queue)->Data; // 큐 전단 정점 제거
E = V->AdjacencyList;
while (E != NULL) // 제거한(Dequeue) 정점의 인접 정점들에 대해서
{
if (E->Target != NULL && E->Target->Visited == NotVisited) // 인접정점중 방문하지 않은정점
{
E->Target->Visited = Visited; // 방문함으로 변경
printf("%d ", E->Target->Data);
LQ_Enqueue(Queue, LQ_CreateNode(E->Target)); // 큐에 넣기
}
E = E->Next; // 다음 인접정점
}
}
}위상정렬(Topological Sort)
- 위상 : 어떤 정점이 다른 정점과의 관계속에서 가지는 위치
- 순서가 있는 작업을 차례대로 수행해야 할 때 작업 순서 결정 ex) 선수과목
- 위치는 간선 방향에 의해 결정됨 (앞) -> (뒤) : 간선을 뻗어내는 정점이 앞 간선을 받아들이는 정점이 뒤
위상정렬은 DAG(Directed Acyclic Graph) 그래프 에서만가능DAG Graph : 그래프에 방향성이 있고 그래프내에 사이클이 없는 그래프
위상 정렬의 동작방식
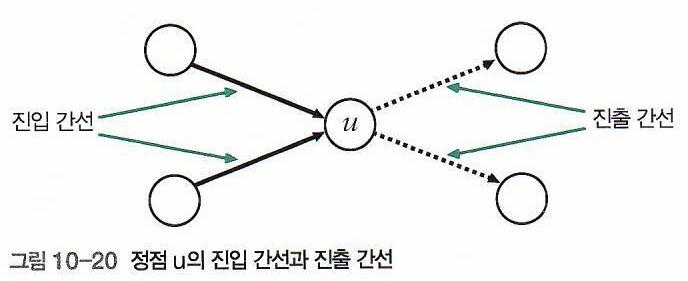
- 진입간선 : 정점으로 들어가는 간선
- 진출간선 : 정점으로 나가는 간선
- 한 정점에 진입간선이 있다? -> 이 정점 이전단계에 정점이 있다.
- 한 정점에 진출간선이 있다? -> 이 정점 다음단계의 정점이 있다.
위상정렬 알고리즘 1
- 리스트의 앞에서 부터 채우는 알고리즘 (새로운 정점을 리스트 테일에 추가)
- 진입간선이 없는 정점을 리스트에 추가하고 해당 정점자신과 진출간선 제거 (진입간선이 없다? -> 이전에 해야하는 일이 없다. -> 맨 앞에 해도 된다.)
위상정렬 알고리즘 2
- 리스트의 뒤에서 부터 채우는 알고리즘 (새로운 정점을 리스트 헤드에 추가)
- 그래프에서 진입 간선이 없는 정점에대해 깊이 우선 탐색 시행, 탐색중 더이상 옮겨갈 수 있는 인접정점이 없으면(진출 할수 없으면) 그 정점을 리스트의 새로운 헤드로 입력
- 진출할 수 없다? -> 지금 이 작업이 마지막으로 해야할 작업. -> 뒤에 삽입
한 노드에서 DFS를 시작하더라도 모든 노드를 방문할 수 있는 것은 아닙니다.
서로 연결되지 않는 두 그래프가 있다면, 한 그래프에서 시작한 DFS는 다른 그래프로 방문할 수 없습니다.
한 그래프에 있더라도, 방향 그래프인 경우 두 노드가 연결될 수 없는 경우도 존재합니다.
예를 들어 DAG(Directed Acyclic Graph, 유향 비순환 그래프) 의 중간에서 DFS를 시작하면,
시작 노드로 들어오는 엣지는 방문하지 못하기 때문에 모든 노드를 방문할 수 없습니다.
https://stlee321.tistory.com/entry/%EA%B7%B8%EB%9E%98%ED%94%84-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98DFS-%EA%B9%8A%EC%9D%B4-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89
최소 신장 트리 (Minimum Spanning Tree)
- 신장트리: 그래프의 모든 정점을 연결하는 트리
- 최소신장트리: 가중치의 합이 최소가 되는 간선만 남긴 신장트리
Prim`s Algorithm
- 최소 신장 트리에 연결된 정점들의 주변 정보를 파악하여 최소 신장 트리를 완성내나감
- 임의정점을 시작 정점으로 하여 MST 뿌리 노드로 삽입
- 최소 신장 트리의 인근 노드들중 최소 신장 트리로 부터 가장 가중치가 작은 간선으로 연결된 노드를 삽입 (다만 사이클을 형성하면 안된다)
- 모든 정점이 연결되면 알고리즘 종료
- 최소 가중치를 가진 간선을 찾아내기 위해 우선 순위 큐 사용
void Prim(Graph* G, Vertex* StartVertex, Graph* MST) {
int i = 0; // index를 나타내기 위한 값
PQNode StartNode = { 0,StartVertex }; // {우선순위, 값}
PriorityQueue* PQ = PQ_Create(10); // PQ는 유동적으로 사이즈 조절 할 수 있음.
Vertex* CurrentVertex = NULL; // 현재 pop한 노드를 저장할 변수
Edge* CurrentEdge = NULL;
// 각정점들의 tree로 부터의 가중치를 저장할 배열
int* Weights = (int*)malloc(sizeof(int) * G->VertexCount);
// MST의 정점들을 인덱스에 따라 저장할 배열
Vertex** MSTVertices = (Vertex**)malloc(sizeof(Vertex*) * G->VertexCount);
// 색칠된 정점 즉 MST에 추가된게 확실해 더이상 확인 하지 않아도 되는 정점을 체크
Vertex** Fringes = (Vertex**)malloc(sizeof(Vertex*) * G->VertexCount);
// 한 정점의 부모 정점을 저장한 배열 : 한 정점의 인덱스를 주면 그 정점의 부모 정점을 바로 얻어낼 수 있다
Vertex** Precedences = (Vertex**)malloc(sizeof(Vertex*) * G->VertexCount);
CurrentVertex = G->Vertices; // MST를 만들 그래프의 정점 목록 가져오기
while (CurrentVertex != NULL) // 정점 등록 + 체크해야할 사항들을 초기값으로 초기화
{
Vertex* NewVertex = CreateVertex(CurrentVertex->Data);
AddVertex(MST, NewVertex);
Weights[i] = MAX_WEIGHT; // 무한대로 설정 (실제 코드에서는 충분히 큰 수로 표현)
MSTVertices[i] = NewVertex; // 인덱스에 맞는 정점
Fringes[i] = NULL;
Precedences[i] = NULL; // 아직 정해지지 않았으므로 null로 초기화
CurrentVertex = CurrentVertex->Next; // 다음 인덱스의 정점
i++;
}
PQ_Enqueue(PQ, StartNode);
Weights[StartVertex->Index] = 0; // 시작 노드에 대한 처리.
while (!PQ_IsEmpty(PQ)) // 간선 내용들 업데이트 -> 실질적인 MST 만드는 과정
{
PQNode Popped;
PQ_Dequeue(PQ, &Popped); // pq 최상단 노드 pop 해옴
CurrentVertex = Popped.Data;
CurrentEdge = CurrentVertex->AdjacencyList;
Fringes[CurrentVertex->Index] = CurrentVertex; // MST에 노드 들어감 -> 색칠됨
while (CurrentEdge != NULL)
{
Vertex* TargetVertex = CurrentEdge->Target;
// 아직 정점을 방문하지 않았고 알려진 가중치보다 새롭게 발견한 트리로부터의 가중치가 작다면
if (Fringes[TargetVertex->Index] == NULL && Weights[TargetVertex->Index] > CurrentEdge->Weight)
{
PQNode NewNode = { CurrentEdge->Weight,TargetVertex };
PQ_Enqueue(PQ, NewNode);
Weights[TargetVertex->Index] = CurrentEdge->Weight; // 가중치 업데이트
Precedences[TargetVertex->Index] = CurrentEdge->From; // 그 노드의 부모 업데이트
}
CurrentEdge = CurrentEdge->Next;
}
}
for (int i = 0; i < G->VertexCount; i++) // 간선 정보들을 이용해 간선만들기
{
int FromIndex = 0; int Toindex = 0;
if (Precedences[i] == NULL)
continue;
FromIndex = Precedences[i]->Index;
Toindex = i;
// 양방향으로 연결
AddEdge(MSTVertices[FromIndex], CreateEdge(MSTVertices[FromIndex], MSTVertices[Toindex], Weights[i]));
AddEdge(MSTVertices[Toindex], CreateEdge(MSTVertices[Toindex], MSTVertices[FromIndex], Weights[i]));
}
free(Weights);
free(MSTVertices);
free(Precedences);
free(Fringes);
PQ_Destroy(PQ);
}Kruskal`s Algorithm
- 간선의 모든 가중치 정보를 사전에 파악하고 이 정보를 토대로 최소 신장 트리 구축
- 그래프내의 모든 간선을 가중치의 오름차순으로 정렬(또는 PQ사용)
- 간선의 목록을 순회하면서 간선을 최소신장트리에 추가 단 사이클을 형성하면 안됨.
- 사이클 탐지 문제 -> 분리집합으로 해결
간선으로 연결된 정점들에 대해 합집합 수행 이때 간선으로 이을 두 정점이 같은 집합에 속해있다면 사이클 발생
void Kruskal(Graph* G, Graph* MST)
{
int i = 0;
Vertex* CurrentVertex = NULL;
Vertex** MSTVertices = (Vertex**)malloc(sizeof(Vertex*) * G->VertexCount); // 정점목록
DisjointSet** VertexSet = (DisjointSet**)malloc(sizeof(DisjointSet*) * G->VertexCount); // 정점 갯수만큼의 분리집합 필요
PriorityQueue* PQ = PQ_Create(10); // 가장 가중치가 낮은 간선을 뽑아내기 위한 PQ
CurrentVertex = G->Vertices;
while (CurrentVertex != NULL)
{
Edge* CurrentEdge;
VertexSet[i] = DS_MakeSet(CurrentVertex); // 정점마다 분리집합 생성
MSTVertices[i] = CreateVertex(CurrentVertex->Data); // 정점 등록
AddVertex(MST, MSTVertices[i]);
CurrentEdge = CurrentVertex->AdjacencyList;
while (CurrentEdge != NULL) { // 모든 정점의 모든 간선을 PQ에 추가
PQNode newNode = { CurrentEdge->Weight,CurrentEdge };
PQ_Enqueue(PQ, newNode);
CurrentEdge = CurrentEdge->Next;
}
CurrentVertex = CurrentVertex->Next;
i++;
}
while (!PQ_IsEmpty(PQ))
{
PQNode Poped;
Edge* CurrentEdge = NULL;
int Fromindex = 0;
int Toindex = 0;
PQ_Dequeue(PQ, &Poped);
CurrentEdge = Poped.Data;
Fromindex = CurrentEdge->From->Index;
Toindex = CurrentEdge->Target->Index;
if (DS_FindSet(VertexSet[Fromindex]) != DS_FindSet(VertexSet[Toindex])) { // 간선 양 끝에 있는 정점이 같은 부분집합에 속해있는지 확인
AddEdge(MSTVertices[Toindex], CreateEdge(MSTVertices[Toindex], MSTVertices[Fromindex], CurrentEdge->Weight));
AddEdge(MSTVertices[Fromindex], CreateEdge(MSTVertices[Fromindex], MSTVertices[Toindex], CurrentEdge->Weight));
DS_UnionSet(VertexSet[Fromindex], VertexSet[Toindex]); // 간선을 연결했다면 합집합
}
}
for (int i = 0; i < G->VertexCount; i++)
{
DS_DestroySet(VertexSet[i]);
}
free(VertexSet);
free(MSTVertices);
}최단 경로 탐색
- 그래프 내의 한 정점에서 다른 정점으로 이동할 때 가중치 합이 최솟값인 경로를 찾는 알고리즘
Dijkstra`s Algorithm
- 프림알고리즘과 비슷한 방식으로 동작
- 차이점 : 정점이 가진 거리 정보가 트리로 부터의 거리가 아닌 시작 정점으로 부터의 거리
- 사이클이 없는 방향성 그래프에서만 사용 가능
- 각 정점은 시작점으로 부터 자신에게 이르는 거리를 저장할 곳 준비 초기값은 무한대(실제로는 매우 큰 수)
- 시작 정점은 0으로 초기화
- 최단 경로에 새로 추가된 정점의 인접 정점에 대해 경로 길이 갱신, 이들을 최단 경로에 추가
- 만약 추가하려는 인접 정점이 이미 최단 경로 안에 있다면 갱신 되기 이전의 경로 길이가 새로운 경로 길이보다 더 큰 경우에 한해 다른 선행 정점을 지나던 기존 경로를 현재 정점을 경유하도록 수정
- 그래프내의 모든 정점이 소속 될 때 까지 반복
void Dijkstra(Graph* G, Vertex* StartVertex, Graph* ShortestPath )
{
int i = 0;
PQNode StartNode = { 0, StartVertex };
PriorityQueue* PQ = PQ_Create(10);
Vertex* CurrentVertex = NULL;
Edge* CurrentEdge = NULL;
int* Weights = (int*) malloc( sizeof(int) * G->VertexCount );
Vertex** ShortestPathVertices =
(Vertex**) malloc( sizeof(Vertex*) * G->VertexCount );
Vertex** Fringes = (Vertex**) malloc( sizeof(Vertex*) * G->VertexCount );
Vertex** Precedences = (Vertex**) malloc( sizeof(Vertex*) * G->VertexCount );
CurrentVertex = G->Vertices;
while ( CurrentVertex != NULL )
{
Vertex* NewVertex = CreateVertex( CurrentVertex->Data );
AddVertex( ShortestPath, NewVertex);
Fringes[i] = NULL;
Precedences[i] = NULL;
ShortestPathVertices[i] = NewVertex;
Weights[i] = MAX_WEIGHT;
CurrentVertex = CurrentVertex->Next;
i++;
}
PQ_Enqueue ( PQ, StartNode );
Weights[StartVertex->Index] = 0; // 시작노드에서 시작노드까지의 거리는 0
while( ! PQ_IsEmpty( PQ ) )
{
PQNode Popped;
PQ_Dequeue(PQ, &Popped);
CurrentVertex = (Vertex*)Popped.Data;
Fringes[CurrentVertex->Index] = CurrentVertex;
CurrentEdge = CurrentVertex->AdjacencyList;
while ( CurrentEdge != NULL )
{
Vertex* TargetVertex = CurrentEdge->Target;
// 아직 방문하지 않았고
// 이웃정점의 알려진 거리의 합이 새롭게 발견한 경로의 가중치합보다 크다면 업데이트
if ( Fringes[TargetVertex->Index] == NULL &&
Weights[CurrentVertex->Index] + CurrentEdge->Weight <
Weights[TargetVertex->Index] )
{
PQNode NewNode = { CurrentEdge->Weight, TargetVertex };
PQ_Enqueue ( PQ, NewNode );
Precedences[TargetVertex->Index] = CurrentEdge->From; // 부모 노드 업데이트
// 정점의 가중치 + 엣지 가중치 = 엣지 끝의 정점의 가중치
Weights[TargetVertex->Index] =
Weights[CurrentVertex->Index] + CurrentEdge->Weight; // 더 작은값으로 업데이트
}
CurrentEdge = CurrentEdge->Next;
}
}
for ( i=0; i<G->VertexCount; i++ )
{
int FromIndex, ToIndex;
if ( Precedences[i] == NULL )
continue;
FromIndex = Precedences[i]->Index;
ToIndex = i;
// 방향성 그래프이므로 prim과 다르게 하나의 edge만 만듦
AddEdge( ShortestPathVertices[FromIndex],
CreateEdge(
ShortestPathVertices[FromIndex],
ShortestPathVertices[ToIndex],
Weights[i] ) ); // 여기서의 weight는 시작정점으로부터의 거리
}
free( Fringes );
free( Precedences );
free( ShortestPathVertices );
free( Weights );
PQ_Destroy( PQ );
}
- 경로 출력은 경로 끝 노드부터 back tracking하여 찾는다 .
연습문제
- 정점의 집합과 그 정점들을 연결한 간선의 집합의 모음
- 경로는 한 정점으로 부터 다른 정점까지 가는데 거쳐야 하는 정점들을 나열, 사이클은 어느 경로가 한 정점을 두번거치게 되어 있다면 그 경로를 사이클이라고 한다. 사이클은 경로의 부분집합.
- 생략
- 1, 2, 5, 4, 3, 6, 7, 8
- 1, 2, 3, 6, 8, 7, 5, 4
- 1, 4, 2, 5, 3, 6, 8, 7
정리가 잘 된 글이네요. 도움이 됐습니다.