동적계획 알고리즘
그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘이다.
해를 구하는데 부분문제들을 중복사용, -> 부분문제들 사이에 의존적 관계존재
5.1 모든 쌍 최단경로 (All Pairs Shortest Paths)
문제를 해결하려면 다익스트라 알고리즘을 사용해도된다. 하지만 플로이드 알고리즘을 사용하면 시간복잡도는 O(n^3)으로 동일하지만, 매우 간단하기 때문에 더 사용하기 효율적이다.

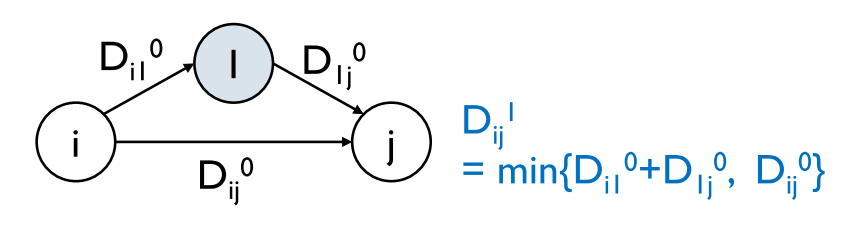
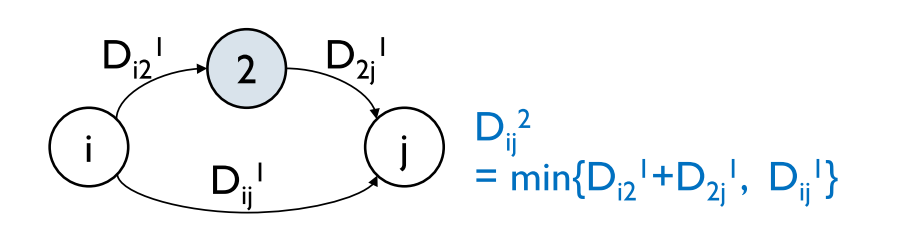
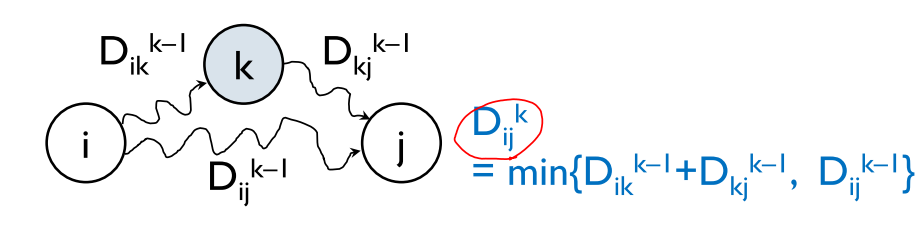
이 과정에서 음수 사이클이 있으면 안된다.
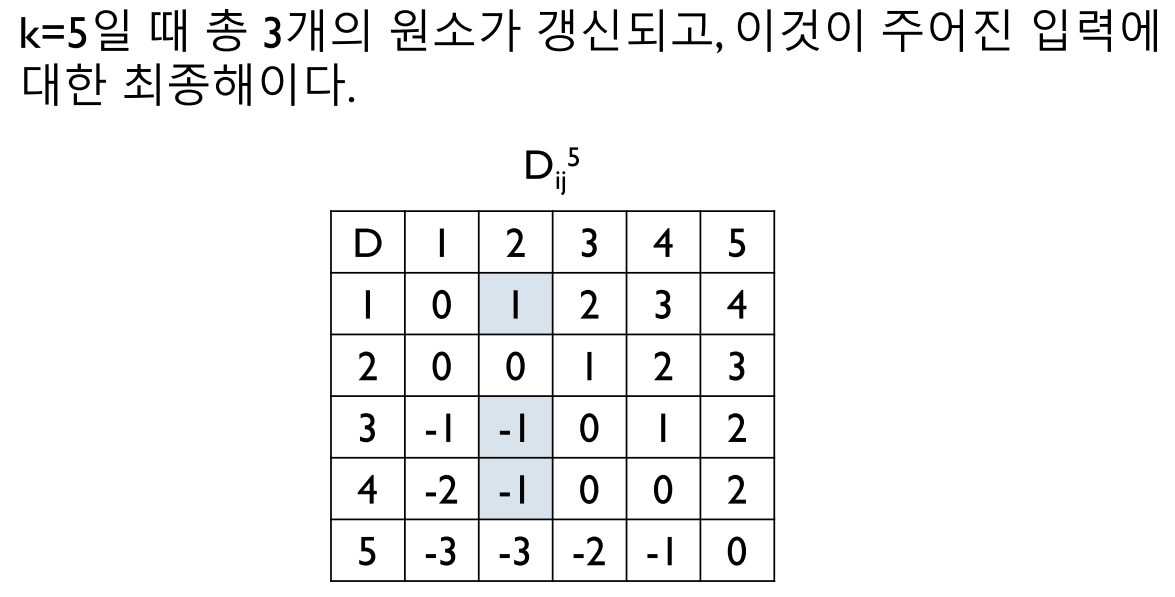
시간복잡도는 각 k에 대해서 모든 i, j 쌍에 대해 계산되므로, n x n x n 이므로 O(n^3)이다.
5.2 연속 행렬 곱셈
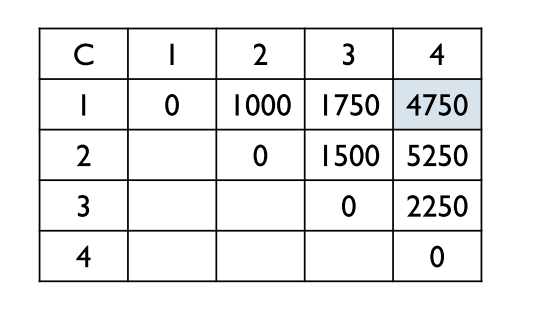
연속된 행렬들의 곱셈에 필요한 원소 간의 최소 곱셈 횟수를 찾는 문제이다.
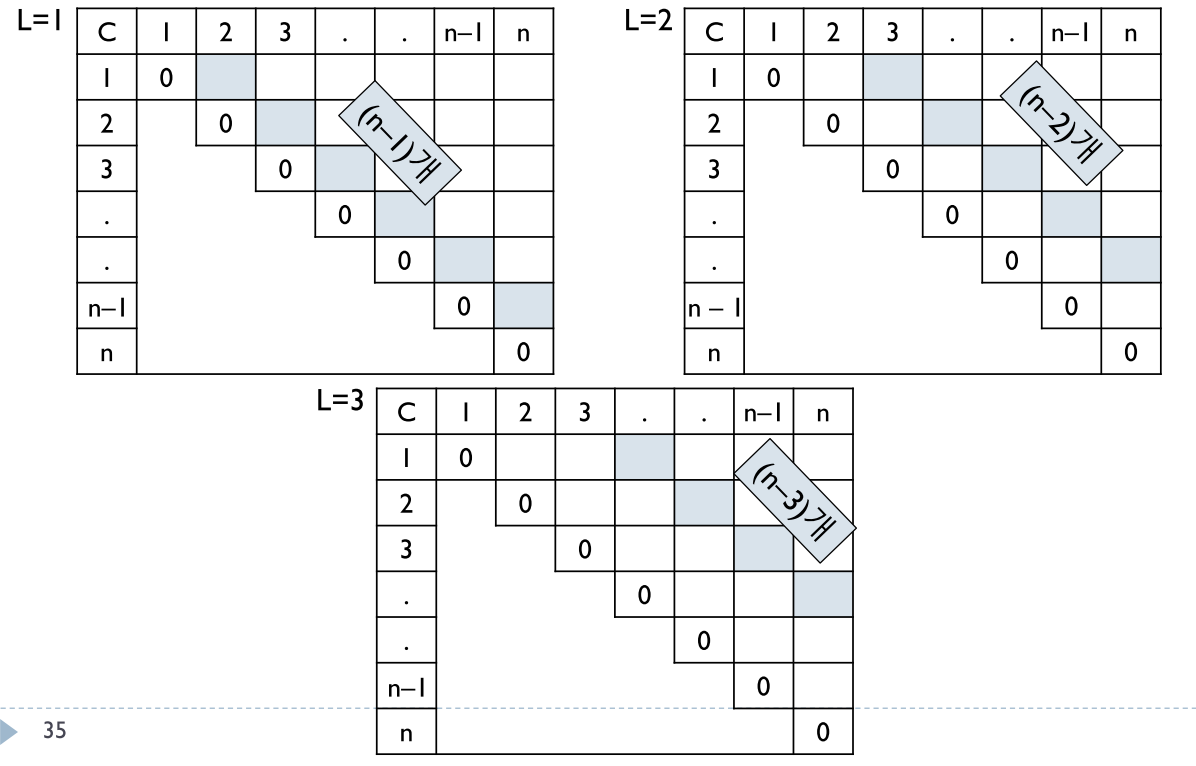
L은 부분문제의 크기. (n - 1)은 부분문제의 개수
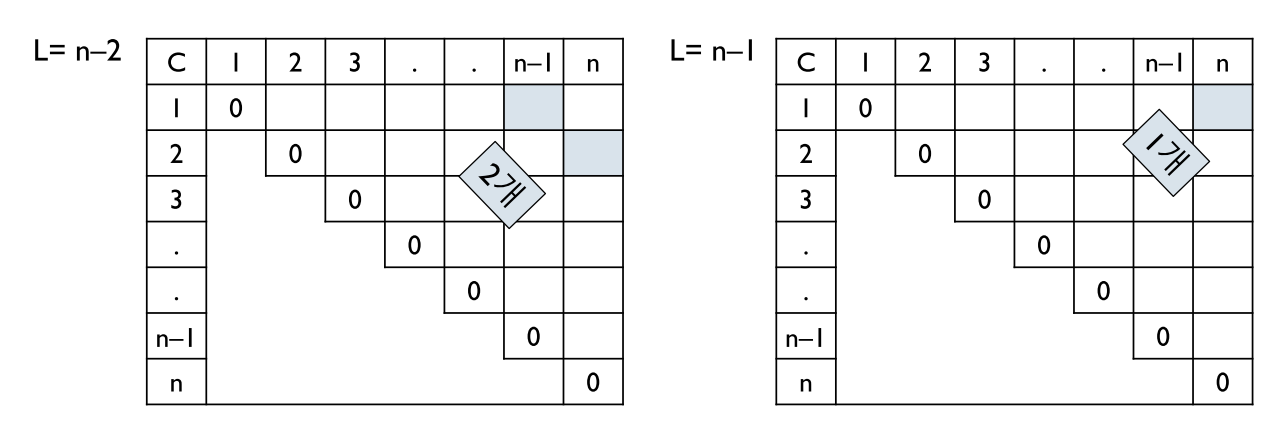
마지막 부분해를 구할 때는 부분문제의 개수가 3개임을 기억.
시간복잡도는 O(n^2) x O(n) = O(n^3)이다.
5.4 배낭 문제
그리디 알고리즘에서 했던 배낭문제와 같다. 다른 점은 동적 계획 알고리즘을 사용한다는 점과, 0 - 1 배낭문제라는 점이다.
배낭문제는 제한적인 입력에 대해서 DP로 해결할 수 있다.

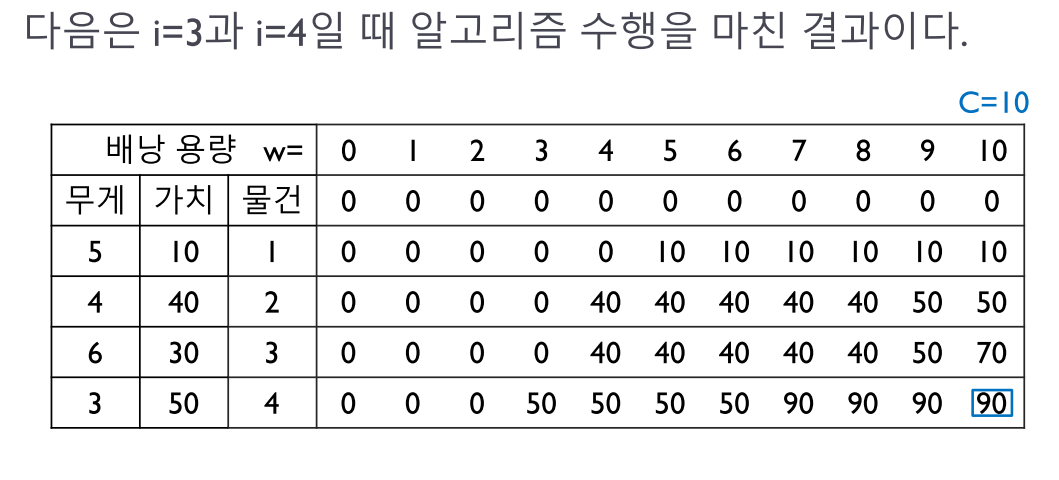
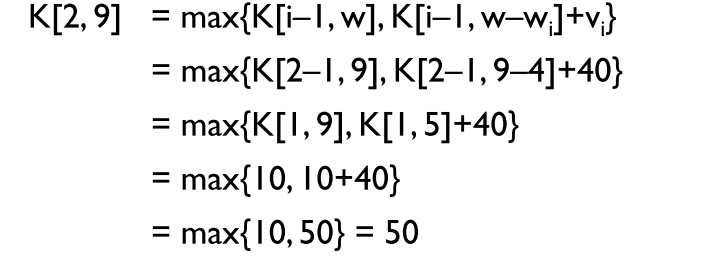
max값을 고를 때 바로 위에 값 혹은 현재의 무게에서 물건의 무게를 뺀 값으로 돌아가서 가치를 더해준 값 사이에서 비교한다.

5.5 동전 거스름돈
적은 수의 동전으로 거스름돈을 받자. DP에서의 동전 거스름돈은 항상 최적해를 찾는다.

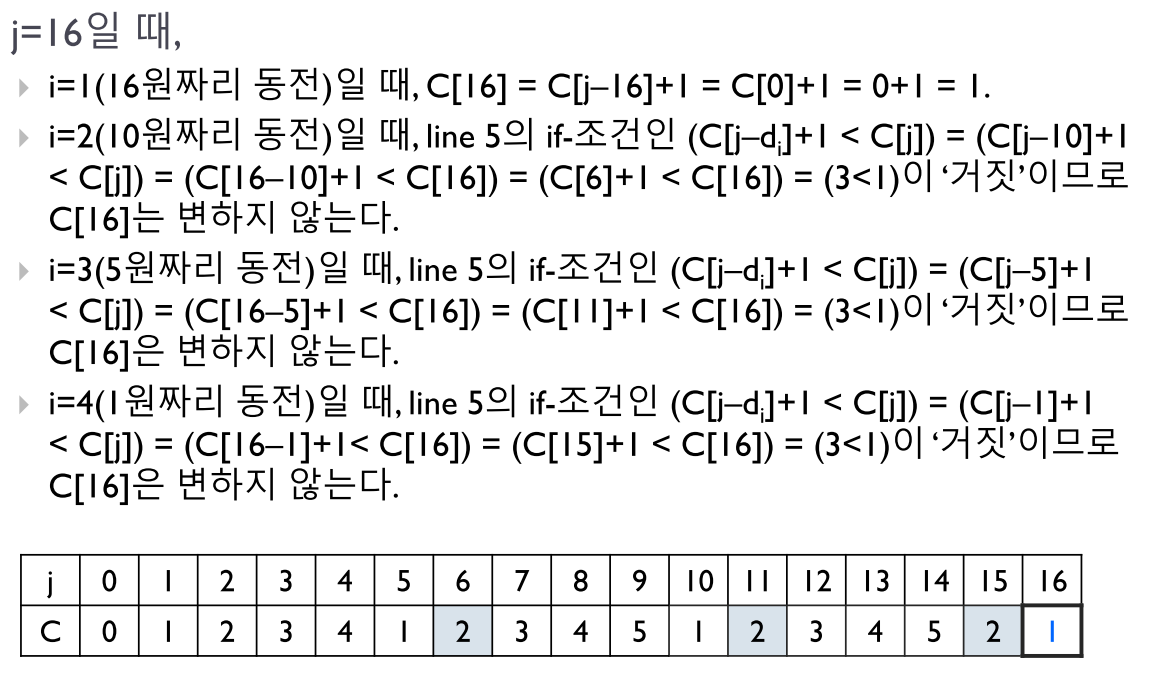
i = 동전
i 값에 따라 부분문제를 나눠 MIN 값이 부분해가 되는게 핵심이다.

