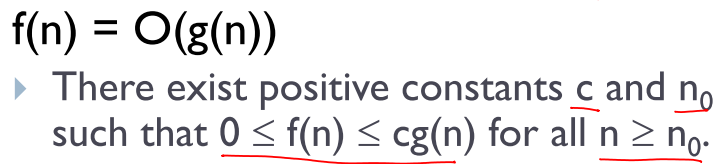알고리즘 Part.2

2.2 최초의 알고리즘

가장 오래된 알고리즘 : 유클리드(Euclid) 의 최대공약수 알고리즘

2개의 자연수의 최대공약수는 큰 수에서 작은 수를 뺀 수와 작은 수와의 최대공약수와 같다는 성질을 이용했다.

의사코드 (Pseudo Code)는 위와 같다.

2.5 알고리즘의 효율성 표현

알고리즘의 효율성은 수행 시간 또는 알고리즘이 수행하는 동안 사용되는 메모리 공간의 크기로 나타낼 수 있다.

• 시간복잡도 (time complexity)
  기본적인 연산 횟수를 입력 크기에 대한 함수로 표현한다.
• 공간복잡도 (space complexity)

알고리즘의 복잡도 표현 방법

• 최악 경우 분석 (worst case analysis) -> 보통 최악의 경우를 생각한다.
• 평균 경우 분석 (average case analysis)
• 최선 경우 분석 (best case analysis)

점근적 표기

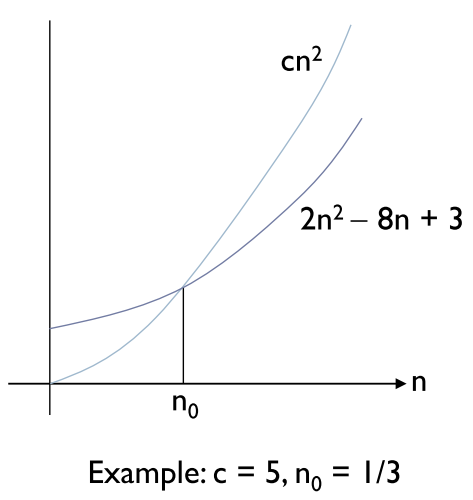
• Big - Oh
  점근적 상한을 나타내며 , 최고 차항만 계수 없이 단순화해서 나타낸다.
  ex) cn^2 -> n^2 (단, c > 0)
  
  
  -> cg(n)이 n0 보다 큰 모든 n에 대해서 항상 f(n)보다 크다.

• Big - Omega
  복잡도의 점근적 하한을 의미한다. 마찬가지로 최고 차항만 계수 없이 단순화해서 나타낸다.
  -> cg(n)이 n0 보다 큰 모든 n에 대해서 항상 f(n)보다 작다.

• Big - Theta
  Big-oh와 Big-Omega의 표기가 같은 경우에 사용한다.

Big-Oh 수행시간 순서

O (1) : 상수시간 (Constant time)
O (log n) : 로그 시간 (Logarithmic time)
O (n) : 선형 시간 (Linear time)
O (n log n) : 로그 선형 시간 (Log Linear time)
O (n^2) : 제곱 시간 (Quadraic time)
O (n^3) : 세제곱 시간(Cubic time)
O (2^n) : 지수 시간 (Exponential time)

효율 적인 알고리즘은 값비싼 HW의 개발 보다 더 경제적이다.