Recursive deep models for semantic compositionality over a sentiment treebank(2013) 논문 읽기①

AI Scientist를 목표로!·2022년 11월 26일

해당 논문은 2013년에 발표된 논문으로 RNTN에 대해서 설명하고 있습니다.

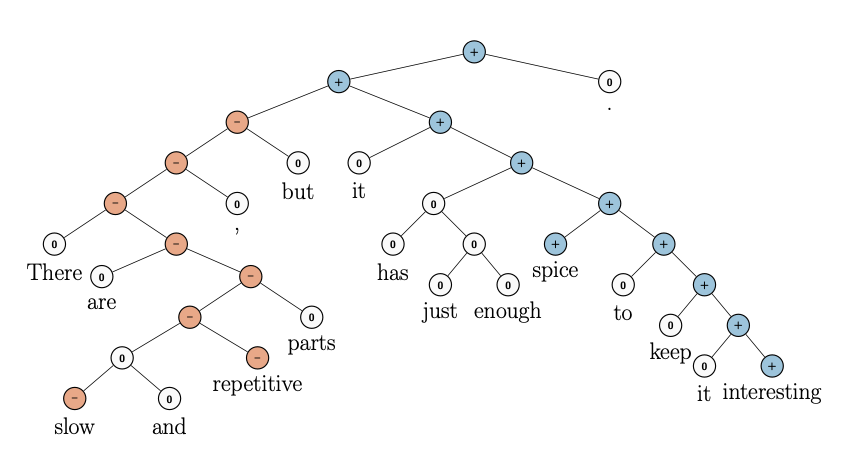
RNTN의 입력값은 문장이 단어, 구(phrase) 단위로 파싱(parsing)되어 있고 단어마다 긍정, 부정이 태깅돼 있는 형태입니다. 양극성이라는 레이블 정보가 주어져 있는 파싱 트리를 기반으로 단어나 구를 Vector로 Embedding하고, 이 Vector를 기반으로 label을 예측하는 모델입니다.

논문을 읽으며 중요하닥 생각되는 부분을 번역하고 적어 놓는 것을 목표로 하고 있습니다.
(영문으로 인해 번역이 다소 이상하고, 문장이 끊기는 느낌을 받을 수도 있습니다ㅠ)

0. Abstract

기존의 Semantic word spaces는 매우 유용했으나, 의미론적으로 긴 문장에서는 표현할 수 없다는 한계점이 존재한다.

감정 감지와 같은 구성성을 이해하는 영역의 발전을 위해서는 더 많은 지도 훈련, 평가 자원, 더 효과적인 모델의 구성을 필요로 한다.

이러한 문제를 해결하기 위해 본 논문은 Sentiment Treebank를 소개한다.

Sentiment Treebank의 문제를 해결하기 위해 Recursive Neural Tensor Network을 같이 소개한다.

RNTN은 이전 모든 방식을 능가하며 긍부정 분류는 80%에서 85.4%로 끌어올릴 수 있었다.

또한 모든 구문에 대한 세분화된 감정 레이블의 예측 정확도는 80.7%로 이전 보다 9.7% 향상 되었다.

마지막으로, 모든 긍부정 문구에 대해 다양한 Tree level에서 부정의 효과와 범위를 정확하게 포착할 수 있는 유일한 모델이다.

1. Introduction

한 단어의 Semantic vector spaces는 feature로 광범위 하게 사용 되었으나, 긴 문장에 대해서는 의미를 파악하지 못하는 단점이 있다.

이를 해결하기 위해 새로운 말뭉치에 존재하는 구성적 의미 효과를 정확하게 예측할 수 있는 Stanford Sentiment Treebank와 RNTN을 소개한다.

Stanford Sentiment Treebank는 언어에서 감정의 구성 효과를 완벽하게 분석할 수 있는 완전한 레이블이 지정된 최초의 말뭉치이다.

해당 말뭉치는 영화 리뷰에서 추출한 11,885개의 단일 문장이며, Parse Tree에는 총 215,154개의 고유한 문구를 포함하고 있다.

RNTN은 임의의 길이를 입력 구문으로 사용되며, Word Vector와 Parse Tree를 통해 구문을 표현한 다음 동일한 Tensor기반 구성 함수를 사용하여 Tree의 상위 노드에 대한 Vector를 계산한다.

RNN, matrix-vector RNN, NB, bi-gram NB, SVM 등 다양한 모델과 비교 했을 때, 모든 모델은 새로운 데이터(=스탠포드 감성 트리 말뭉치)로 훈련 시 크게 향상이 되지만, RNTN는 세분화된 감정을 예측할 때, 80.7%의 정확도로 최고의 성능을 보인다.

또한 RNTN은 감정 변화와 부정의 범위를 정확하게 포착한다.

3. Stanford Sentiment Treebank

원래 데이터 세트에는 10,662개의 문장이 포함되어 있으며, 긍부정은 반반으로 구성되어 있다.

독자들의 통찰력을 기반으로한 문장 라벨링 과정 속에서 알아차린것들 중 하나는 많은 부분(문장)들이 중립적인 것으로 간주될 수 있다는 것이다.

또한 더 강한 감정은 종종 더 긴 문장으로 축적되고, 짧은 문장에서는 대부분 중립적이다는 것을 알 수 있었다.

4. Recursive Neural Models

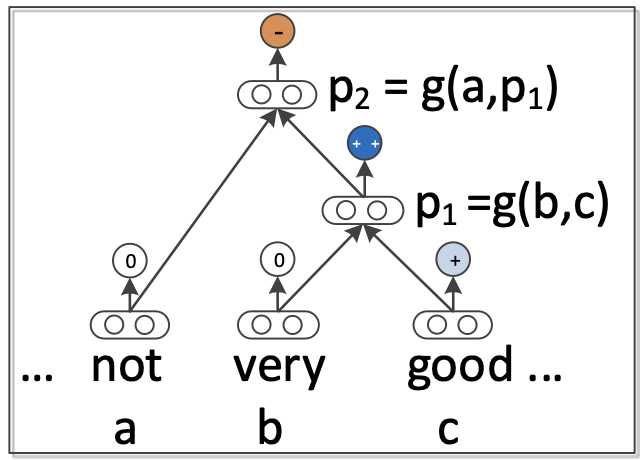
N-gram이 주어지면 이진 트리로 문장이 분석되고 각 단어에 해당하는 각 leaf 노드가 Vector로 표현된다.

아래에서 부터 상향식으로 구성 함수를 $g$ 를 사용해 부모 Vector를 계산한다.

부모 Vector는 다시 분류를 위한 Feature로 사용된다.

각 단어는 $d$ 차원의 Vector로 표시되며,
모든 단어 Vector는 단어 Embedding 행렬 $R^{d×|V|}$ 로 축척되고, 행렬 matrix는 훈련용 매개변수로 간주된다.
( $|V|$ 는 vocab_size)

단어 Vector는 매개 변수 최적화와 softmax 분류를 위한 input feature로 즉시 사용할 수 있으며 5개의 클래스로 분류하기 위해 $y^a = softmax(W_sa)$ 를 통해 확률을 계산하게 된다.

4-1. RNN: Recursive Neural Network

신경망 모델들의 가장 단순한 구성은 RNN이다.

첫째, 부모 node가 모든 자녀 node를 계산하도록 결정한다.

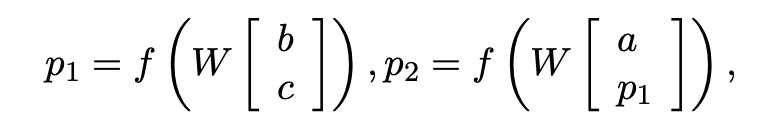
RNN은 위 방정식을 통해 상위 Vector를 계산한다.

$f$ 는 tanh이며 standard element-wise nonlinearity 이며,
$W ∈ R^{d×2d}$ 는 주요 매개 변수이며 단순성을 위해 bias를 생략한다.

RNN은 재귀 Auto-Encoder와 재귀 Auto-associate memories와 동일한 구성을 사용한다.

$p_1$ 은 b라는 좌측 자식 node와 c라는 우측 자식 node를 위,아래로 붙인(concatenate)(= $W$ ) Vector로 각 자식 node가 $R^d$ 차원의 Vector라면 이 둘이 합쳐진 $R^{2d}$ 차원의 Vector가 됩니다.

부모 Vector는 다음 구성에 대한 input값으로 사용되기 위해 동일한 차원을 가져야 하며, 각 부모 Vector의 파이는 softmax를 통해 분류 됩니다.

다시 $p_1$ 은 또 다른 자식 node가 될 수 있기 때문에 $R^d$ 차원이 됩니다.

4-2. MV-RNN: Matrix-Vector RNN

MV-RNN의 주요 아이디어는 구문 분석 트리의 모든 단어와 긴 구문을 Vector와 Matrix로 표현하는 것이다.

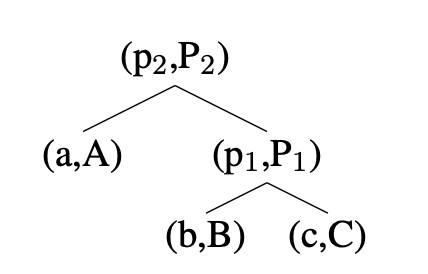
두 구성 요소(= 두 자식 노드)가 결합될 때, 한 Matrix은 다른 행렬의 Vector와 곱하고, 반대의 경우도 동일하게 진행한다.

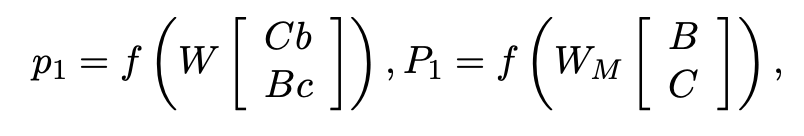
위 그림에서 부모 node $p_1$ 에 대한 자식 node b,c 입니다.

자식 node는 Vector값 (b,c) / Matrix값 (B,C)로 구성되어 있습니다.

$p_1$ 을 먼저 구해보면

부모 node는 좌측 자식 node의 Vector값 b와 우측 자식 node의 Matrix값 C를 내적합니다 (반대의 값도 동일)

해당 결과물을 합쳐(concatenate)(= $W$ ) 이전 RNN과 동일하게 비선형성을 획득하게 됩니다.

이제 $P_1$ 을 구해보면

좌측 node의 Matrix인 B와 우측 node의 Matrix인 C를 합쳐(concatenate)(= $W_M$ ) 생성합니다.

차원의 수는 $P_1 = R^d, W = R^{d×2d}, P_1 = R^{d × d}, W_M = R^{d×2d}$ 입니다.

4-3. RNTN:Recursive Neural Tensor Network

MV-RNN의 한 가지 문제는 매개 변수의 수가 매우 커지고 어휘의 크기에 따라 다르다는 것이다.

고정된 수의 매개변수를 가지는 강력한 Composition Function이 있다면 더 좋을 것이다.

RNTN은 하나의 강력한 Composition Function이 특징들을 가지는 여러개의 input 보다 더 작은 구성요소에서 다 나은 성능과 의미 함축을 더 정확하게 구성할 수있을까? 하는 고민에서 시작 되었다.

RNTN의 주요 아이디어는 모든 node에 동일한 Tensor 기반 Composition Function를 사용하는 것이다.

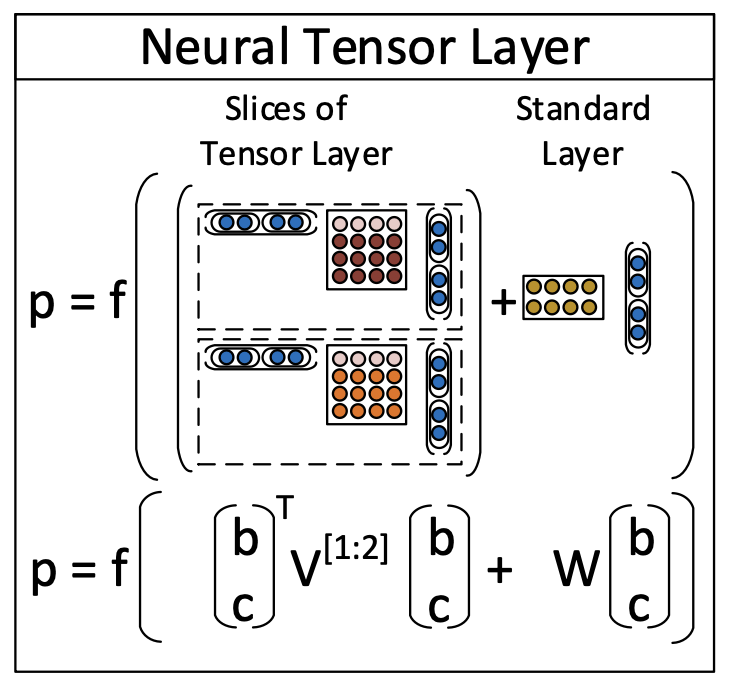
RNTN이 이전 RNN 모델에 비해 주요한 이점은 Tensor가 입력 Vector를 직접 연관시킬 수 있다는 것이다.

직관적으로 봤을 때, Tensor의 각 슬라이스를 특정 유형의 Composition을 수집하는 것으로 해석을 할 수 있다.

4-4. Tensor Backprop through Structure

Target Vector와 Predicted Vector는 one-hot encoding으로 되어 있으며 각 node는 Softmax Classifier를 갖는다.

각각의 node는 Weight 값인 V,W를 반복적으로 사용해 역전파를 한다.

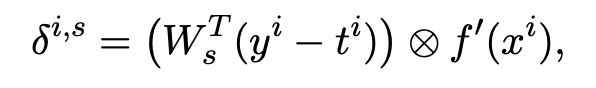
node $i$ 의 Predicted Vector와 Target Vector를 빼준 결과를 Softmax한 후 $W^T$ 와 곱한다.

node $i$ 의 Vector를 tanh인 $f$ 에 파라미터로 주고 미분한다.

1의 결과와 2의 결과물을 Hadamard 곱을 한다.

Hadamard = 두 행렬의 element 중 행과 열이 모두 같은 것 끼리 더해주는 것
일반 행렬은 (m x n)과 (n x m)을 곱해 (m x m)의 값을 산출하지만
아다마르곱은 (m x n)과 (m x n)을 곱해 (m x n)을 산출한다.