WikiDocs를 참조해서 Trnasformer에 대해서 세세하게 정리하는 시간을 가져보려 합니다.
기존 seq2seq의 한계
기존 seq2seq는 Encoder-Decoder 형태로 이루어져 있습니다.
다만, Encoder가 입력 시퀀스를 하나의 Vector로 압축을 하는 과정에서 입력 시퀀스의 정보가 일부 손실된다는 단점이 나타납니다.
이를 보정하기 위해서 Attention을 사용하게 되었습니다.
Attention을 통해서 Encoder-Decoder가 만들어 진것이 Transformer 입니다.
Transformer
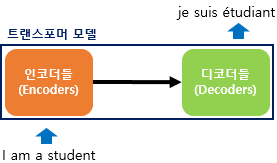
자연어 처리 모델은 텍스트 문장을 입력 받아 임베딩 벡터로 변환하는 과정을 거치게 됩니다.
Transformer도 동일하지만 기존에 seq2seq에서 사용되었던 RNN과는 차이점이 있습니다.
임베딩 벡터에 어떤 임의의 값을 더해준뒤 입력으로 사용하는 것입니다.
이 부분이 포지셔널 인코딩 부분입니다.
포지셔널 인코딩(Positional Encoding)
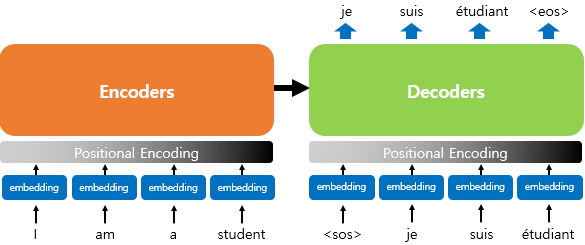
기존 RNN이 자연어 처리에서 강점을 가졌던 것은 단어의 위치에 따라 단어를 순차적으로(시계열)로 입력받아서 처리하는 특성으로 인해 각 단어의 위치 정보를 가질 수 있다는 점이 강점이었습니다.
하지만 Transformer의 경우 단어를 순차적으로 입력받는 것이 아니기 때문에 단어의 위치 정보를 알려줄 필요성이 발생하게 됩니다.
이를 포지셔널 인코딩(Positional Encoding)이라고 합니다.

임베딩 벡터가 Encoder의 입력으로 사용되기 전 포지셔널 인코딩의 값이 더해지는 과정은 위의 그림과 같습니다.
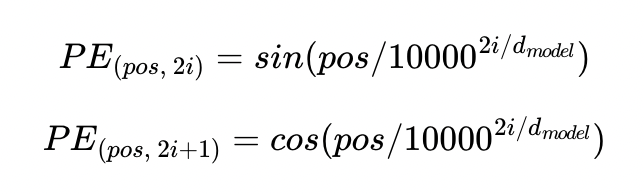
위치 정보를 가진 값을 만들기 위해서는 sin함수와 cos함수를 사용합니다.
sin함수와 cos함수의 값을 임베딩 벡터에 더해주므로 단어의 순서 정보를 추가하는 방법입니다.
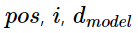
하지만, 위의 식에서는 기존 sin, cos함수와는 다르게 다음과 같은 변수들이 있습니다.
변수들의 의미는 다음과 같습니다.
- : 입력 문장에서의 임베딩 벡터의 위치
- : 임베딩 벡터 내 차원의 인덱스
- 차원의 인덱스가 짝수인 경우에는 sin함수를 사용
- 차원의 인덱스가 홀수인 경우에는 cos함수를 사용
- : Transformer의 모든 출력 차원을 의미하는 Hyper Parameter (논문에서는 512의 값)
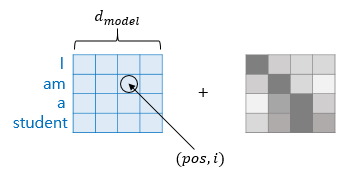
임베딩 벡터와 포지셔널 인코딩의 덧셈의 값은 사실 임베딩 벡터가 모여 만들어진 문장 행렬과 포지셔널 인코딩 행렬의 덧셈 연산을 통해 이루어지게 됩니다.
포지셔널 인코딩의 방법을 사용하면 순서 정보가 보존이 되게 됩니다.
그로인해 각 임베딩 벡터에 포지셔널 인코딩의 값을 더하면 같은 단어라고 하더라도 문장 내의 위치에 따라서 입력으로 들어가는 벡터의 값이 달라지게 되어 순서 정보가 반영이된 임베딩 벡터가 되게 됩니다.
Code로 구현
Transformer의 입력
class PositionalEncoding(tf.keras.layers.Layer):
def __init__(self, position, d_model):
super(PositionalEncoding, self).__init__()
self.pos_encoding = self.positional_encoding(position, d_model)
def get_angles(self, position, i, d_model):
angles = 1 / tf.pow(10000, (2 * (i // 2)) / tf.cast(d_model, tf.float32))
return position * angles
def positional_encoding(self, position, d_model):
angle_rads = self.get_angles(
position=tf.range(position, dtype=tf.float32)[:, tf.newaxis],
i=tf.range(d_model, dtype=tf.float32)[tf.newaxis, :],
d_model=d_model)
# 배열의 짝수 인덱스(2i)에는 사인 함수 적용
sines = tf.math.sin(angle_rads[:, 0::2])
# 배열의 홀수 인덱스(2i+1)에는 코사인 함수 적용
cosines = tf.math.cos(angle_rads[:, 1::2])
angle_rads = np.zeros(angle_rads.shape)
angle_rads[:, 0::2] = sines
angle_rads[:, 1::2] = cosines
pos_encoding = tf.constant(angle_rads)
pos_encoding = pos_encoding[tf.newaxis, ...]
print(pos_encoding.shape)
return tf.cast(pos_encoding, tf.float32)
def call(self, inputs):
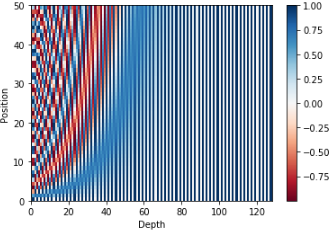
return inputs + self.pos_encoding[:, :tf.shape(inputs)[1], :]- 입력 문장의 단어가 50개 이면서 각 단어가 128차원의 임베딩 벡터를 가지게 되는 즉, 50 x 128의 크기를 가지는 포지셔널 인코딩 행렬을 시각화 하면 다음과 같은 이미지를 가지게 됩니다.
# 문장의 길이 50, 임베딩 벡터의 차원 128
sample_pos_encoding = PositionalEncoding(50, 128)
plt.pcolormesh(sample_pos_encoding.pos_encoding.numpy()[0], cmap='RdBu')
plt.xlabel('Depth')
plt.xlim((0, 128))
plt.ylabel('Position')
plt.colorbar()
plt.show()(1, 50, 128)