선형 탐색 알고리즘

• 왼쪽부터 순서대로 확인하는 방식

• 정렬되지 않은 데이터들을 순차적으로 접근하여 원하는 데이터를 찾는 경우 사용

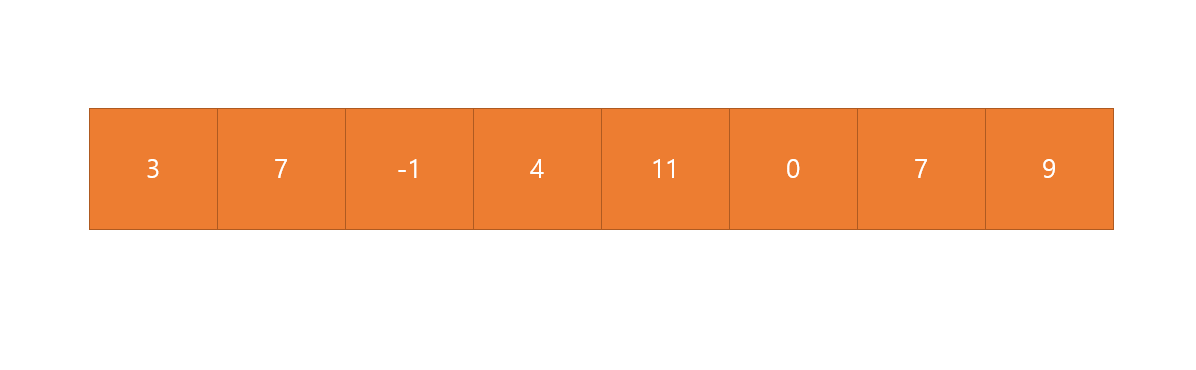
1. 만일 찾고 싶은수가 0이라면 왼쪽부터 0이 있는지 하나씩 탐색

2. 맨 처음 3은 0과 같지 않으므로 그 다음 수인 7, -1, 4, 11을 비교하다가 0을 찾으면 탐색이 종료

• 시간 복잡도 : $O(n)$

---

• 장점

  • 간단하고 구현이 쉬움

  • 목록이 작거나 검색하려는 요소가 목록의 시작 부분에 있을 경우 효울적

  • 목록에 대한 순차적 엑세스만 필요하므로 요소를 반복할 수 있는 모든 데이터 컬럭션에서 작업할 수 있음

• 단점

  • 소요시간이 목록의 크기에 따라 선형적으로 증가

  • 목록이 크거나 찾고자 하는 요소가 뒷부분에 있을 경우 비효율적

---

num = [3, 7, -1, 4, 11, 0, 15, 2, 49]


def linear_search(num, target):
    for i in range(len(num)):
        if num[i] == target:
            return i
    return None

print(linear_search(num, 0))

print(linear_search(num, 50))

이진 탐색 알고리즘

• 전체를 반으로 나눠 대소 비교를 통해 탐색

• 데이터가 정렬되어 있지 않으면 사용이 불가능

• 정렬되어 있는 데이터들을 탐색할 경우 이진 탐색이 더 효율적

• 목록을 한 번 정렬하면 장기적으로 검색 성능이 향상될 수 있으므로 목록이 자주 검색되는 경우에 유용

---

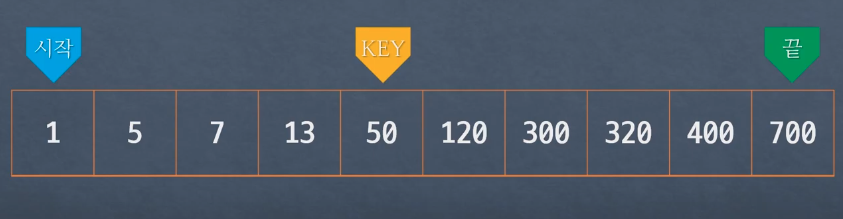
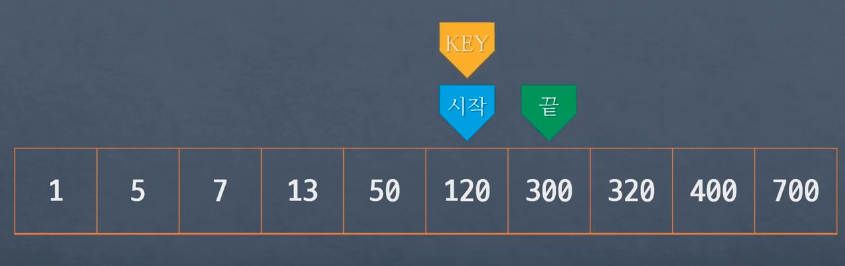
• 시작, 끝, key(가운데) 값이 존재

• target을 V라고 가정할 경우 Key와 V를 비교해서 대소에 따라 상대적 위치 파악

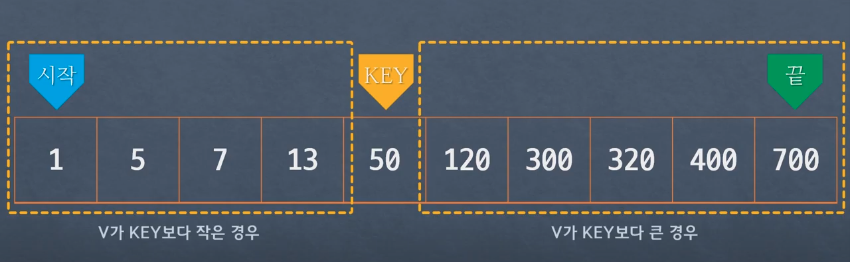
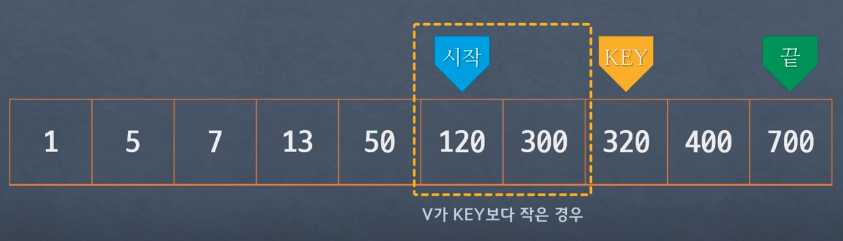
• V가 Key 보다 클 경우 : key + 1의 위치를 시작 위치로 변경하고 시작과 끝 중간에 다시 Key값 설정

• V가 Key 보다 작을 경우 : key - 1의 위치를 끝 위치로 변경하고 시작과 끝 중간에 다시 Key값 설정

• key는 평균의 정수이기 때문에 시작과 끝의 위치가 겹치는 경우

• 찾는 값이 존재 O => End

• 찾는 값이 존재 X => 위치가 겹치는 순간에 한 번 더 진행
  그러면 끝이 시작보다 왼쪽으로 넘어가는 순간이 오게되며, 이상태를 값이 없다고 판단하는 기준이 됨

• 시간 복잡도 : $O(log_n)$

---

• 장점

  • 목록의 크기가 커질수록 목록의 요소를 검색하는데 걸리는 시간이 더 느리게 증가함

  • 정렬된 목록이 크거나 검색되는 요소가 목록의 중앙에 위치할 때 잘 작용

  • 재귀를 사용하여 성능을 최적화할 수 있음

• 단점

  • 목록을 정렬해야 하므로 검색 프로세스에 추가 단계가 필요

  • 선형 검색에 비해 구현하기가 더 복잡함

---

num = [1,5,7,13,50,120,300,320,400,700]

def binary_search(num, target):
    left = 0 # 시작 값
    right = len(num) - 1 # 끝 값
    
    while left <= right:
        mid = (left + right) // 2 # 중간 key 값
        if num[mid] == target:
            return mid 
        # 중간 값이 target 보다 작다면 다음 인덱스로 업데이트해 배열의 왼쪽을 제거
        elif num[mid] < target :
            left = mid + 1
        # 중간 값이 target 보다 크다면 이전 인덱스로 업데이트해 배열의 오른쪽을 제거    
        else : 
            right = mid - 1
    return None

print(binary_search(num, 320))