① 정렬 알고리즘(by Python)

AI Scientist를 목표로!·2023년 3월 28일

알고리즘

정렬 알고리즘

정렬 알고리즘은 n개의 숫자가 입력으로 주어졌을 때, 이를 사용자가 지정한 기준에 맞게 정렬하여 출력하는 알고리즘
하지만 대부분 내부 정렬 라이브러리를 활용하게 되므로 직접 정렬 알고리즘을 사용하는 빈도는 거의 없겠지만, 알고리즘의 특징정도는 알아놔야 본인이 작성한 알고리즘의 시간 복잡도를 계산할 수 있을 것이다.

버블 정렬 = 첫 원소부터 순차로 현재 원소가 그 다음 원소보다 크면 두 원소를 바꿈

선택 정렬 = 배열을 선형 탐색하여 가장 작은 원소를 앞으로 보냄

삽입 정렬 = 적절한 위치에 삽입하는 정렬, 필요할 때만 위치를 바꾸므로 데이터가 정렬 되어 있을 경우 효율적

퀵 정렬 = 임의의 기준 대비 큰 수와 작은 수로 나누는 방식

병합 정렬 = 배열을 절반씩 나누어 각각 정렬하고 합해서 다시 정렬

시간/공간 복잡도는 왜 구하는 것인가?

알고리즘의 성능을 분석하기 위해 사용하는 개념으로,
데이터의 양이 많이지고 처리해야하는 방식의 변화에 따라 많은 시간이 쓰이게 되면서 최적의 알고리즘을 사용하기 위해서 계산한다.

시간 복잡도 = 알고리즘을 수행하는데 연산(산술,대입,비교 등)이 몇번 이뤄지는가?

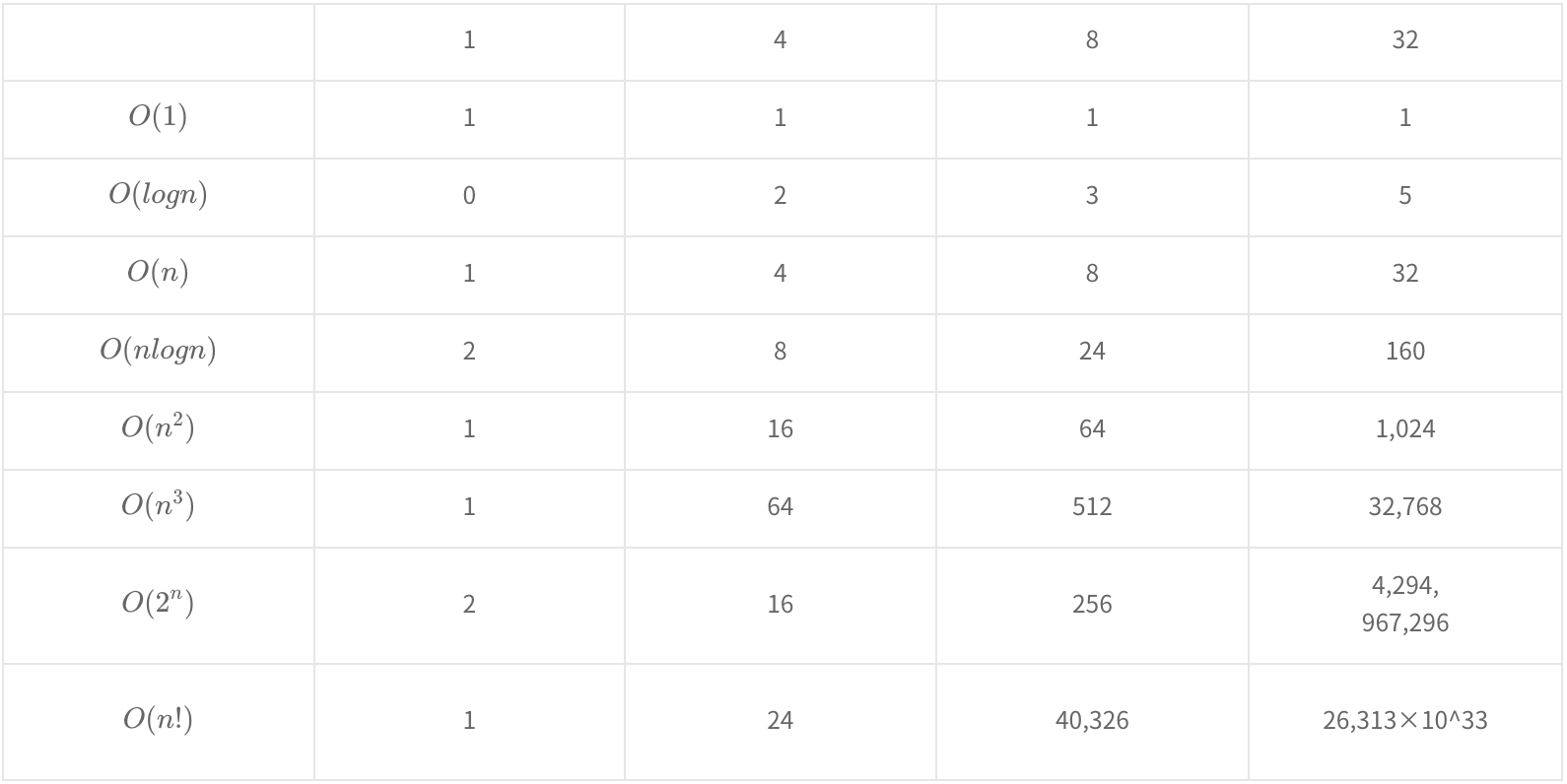
빅오 표기법 = 시간 복잡도를 계산할 때, 상대적으로 불필요한 연산은 제거하여 간편하게 시간 복잡도를 표기하는 방법

공간 복잡도 = 프로그램을 실행시킨 후 완료까지 필요한 자원 공간의 양

총 공간 = 고정 공간 (코드 저장 공간, 단순 변수, 상수 등) + 가변공간 (특정 인스턴스에 의존하는 크기를 가진 구조화 변수, 함수 호출시 추가 공간 등 동적 공간)
S(P) = c + Sp(n)

즉, 시간/공간 복잡도를 이용해 최적의 알고리즘을 찾아야 한다.

버블 정렬

연속된 2개의 인덱스를 비교하여 순서에 따라 정렬하는 방식
n개의 원소에 대하여 n개의 메모리를 사용하며, 대부분의 상황에서 최악의 시간복잡도를 보인다.
공간 복잡도 : $O(n)$
시간 복잡도 : $O(n^2)$

로직

두 번째 인덱스부터 시작하여, 현재 인덱스 값과 바로 이전의 인덱스 값을 비교

만약 이전 인덱스가 더 크면, 현재 인덱스와 변경

현재 인덱스가 더 크면, 교환하지 않고 다음 두 연속된 배열값을 비교

반복

num = [11,234,23,4,1,5,6,2,65,764,825,46,72,47,26,69,793,25,498,245]

def bubble_sort(num):
    n = len(num)
    for i in range(n):
        for j in range(0, n-i-1):
            if num[j] > num[j+1]:
                num[j], num[j+1] = num[j+1], num[j]
    
    return num

print(bubble_sort(num))

선택 정렬

전체 원소들 중에 정렬 위치에 맞는 것을 선택해 해당 위치로 이동시키는 정렬 방식
먼저 주어진 리스트 중에 최소값을 찾고 -> 그 값을 맨 앞에 위치한 값과 교체하는 방식으로 진행
n개의 원소에 대해 n개의 메모리를 사용하기에 데이터를 하나씩 정밀 비교가 가능
교환이 많이 이루어져야하는 자료 상태에서 가장 효율적으로 적용될 수 있는 정렬 방식
내림차순으로 정렬되어 있는 자료를 오름차순으로 재정렬할 때 최적의 효율을 보임
이미 정렬된 상태에서 소수의 자료가 추가됨으로써 재정렬하게 되는 때에는 최악의 처리 속도를 보임
공간 복잡도 : $O(n)$
시간 복잡도 : $O(n^2)$

로직

정렬 되지 않은 인덱스의 맨 앞 부터, 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾음
(정렬되지 않은 인덱스의 맨 앞은, 초기 입력에서의 배열 시작위치)

가장 작은 값을 찾으면, 그 값을 현재 인덱스의 값과 변경

반복

num = [1,2,6,124,6124,23,5,78,24,6,50,9]

def selection_sort(num):
    n = len(num)
    for i in range(n):
        min_idx = i # 기준 값
        for j in range(i+1, n):
            if num[j] < num[min_idx]: # 기준 값의 오른쪽에 있는 하위 배열에서 가장 작은 요소의 인덱스를 찾음
                min_idx = j # 현재 최소 요소보다 작은 요소를 찾았을 경우 변경 
                            # 현재 요소의 오른쪽에 있는 하위 배열에서 가장 작은 요소의 인덱스를 추적하기 원하기 때문
        num[i], num[min_idx] = num[min_idx], num[i]
    return num

print(selection_sort(num))

삽입 정렬

정렬된 집합에 새로운 원소의 적절한 위치를 찾아 삽입하는 정렬 방식
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 정렬 방법
배열이 작을 경우 효율적
공간 복잡도 : $O(n)$
시간 복잡도 : $O(n^2)$

로직

두 번째 인덱스 부터 시작하여, 현재 인덱스는 별도의 변수에 저장해주고, 비교 인덱스를 현재 인덱스 - 1로 설정

별도로 저장해 둔 삽입을 위한 변수와, 비교 인덱스의 배열 값을 비교

삽입 변수의 값이 더 작으면 현재 인덱스로 비교 인덱스의 값을 저장해주고, 비교 인덱스를 - 1 하여 비교를 반복

만약 삽입 변수가 더 크면, 비교 인덱스 + 1에 삽입 변수를 저장

num = [3,2,6,1,124,6124,23,5,78,24,6,50,9]

def insertion_sort(num):
    n = len(num)
    for i in range(1, n): # 두 번째 요소 부터 시작
        key = num[i] # 비교할 기준값
        j = i - 1 # 현재 요소 바로 왼쪽에 있는 요소에서 시작하기 위해 
                  # i - 1에서 시작하여 현재 요소의 왼쪽에 있는 하위 배열에 대해서만 반복하므로 
                  # 비교 횟수가 줄고 알고리즘의 효율성이 향상
        while j >= 0 and key < num[j]:
            num[j + 1] = num[j]
            j -= 1 # 인덱스를 왼쪽으로 한 위치로 이동, 즉, 다음 반복을 위한 루프가 준비
        num[j + 1] = key # 요소가 한 위치 오른쪽으로 이동
    return num

print(insertion_sort(num))

퀵 정렬

합병 정렬과 비슷하게 분할 정복 방식을 이용한 정렬 방식
- 분할 정복 기본 로직
- 1. 현재 배열을 반으로 쪼갠다.
- 1. 배열의 시작 위치와, 종료 위치를 입력 받아 둘을 더한 후 2를 나눠 그 위치를 기준으로 나눈다.
- 1. 이를 쪼갠 배열의 크기가 0이거나 1일때 까지 반복한다.
가장 많이 사용되는 정렬법이지만 안정성이 떨어지는 단점이 존재
공간 복잡도 : $O(n)$
시간 복잡도 : 평균 = $O(nlog_n)$ / 최악 = $O(n^2)$

로직

point로 잡을 배열의 값 하나를 설정 (보통 맨 앞, 맨 뒤, 중간값, 랜덤값)

비교를 진행하기 위해 가장 왼쪽 배열의 인덱스를 저장하는 left 변수
가장 오른쪽 배열의 인덱스를 저장한 right 변수를 생성

right 부터 비교 진행, right가 left 보다 클 때만 반복하며 비교한 배열값이 point 보다 크면 right를 하나 감소시키고 비교 반복

left 비교 진행, right가 left 보다 클 때만 반복하며 비교한 배열값이 point 보다 크면 right를 하나 증가시키고 비교 반복
point 보다 작은 배열 값을 찾으면 반복을 중지

left의 인덱스 값과 right의 인덱스 값을 변경

3,4,5번의 과정을 left < right가 만족할 때 까지 반복

위 과정이 끝나면 left의 값과 point의 값을 변경

맨 왼쪽부터 left-1까지 , left-1부터 맨 오른쪽가지 나눠 퀵 정렬을 반복

num = [3,2,6,1,124,6124,23,5,78,24,6,50,9]

def quick_sort(num):
    # 재귀 알고리즘의 기본 사례로 배열의 길이가 1보다 작거나 같으면 배열이 이미 정렬된 것
    if len(num) <= 1:
        return num
    
    else:
        pivot = num[0] # 맨 앞을 선택
        left = []
        right = []
        # 선택된 값을 제외하고 배열의 나머지 요소를 반복하고 left와 right로 분할
        for i in range(1, len(num)):
            if num[i] < pivot:
                left.append(num[i]) # left는 pivot 보다 작은 값
            else : 
                right.append(num[i]) # right는 pivot 보다 큰 값
    
    # 재귀 알고리즘 적용
    return quick_sort(left) + [pivot] + quick_sort(right)

print(quick_sort(num))

병합 정렬

분할 정복(큰 문제를 반으로 쪼개어 해결해 나가는 방식) 방식을 이용한 정렬 방식
분할 정복 방식에 의해 큰 배열을 크기가 1이 될때가지 반으로 자른 후 잘린 배열을 정렬하여 합침
공간 복잡도 : $O(n)$
시간 복잡도 : $O(nlog_n)$

로직

두 배열 A,B의 크기를 비교한다. (각 배열의 시작 인덱스는 i,j로 가정)

i에는 A 배열의 시작 인덱스를 저장, j에는 B 배열의 시작 인덱스를 저장

A[i]와 B[i]를 비교해, 오름차순의 경우 이중 작은 값을 새 배열 C에 저장

이를 i or j 둘 중 하나가 각자 배열의 끝에 도달할 때 까지 반복

끝까지 저장을 못한 배열의 값을 순서대로 C에 저장

C 배열을 원래의 배열에 저장

num = [3,2,6,1,124,6124,23,5,78,24,6,50,9]

def merge_sort(num):
    if len(num) <= 1:
        return num
    else: 
        mid = len(num) // 2 # 중간값 찾기
        left = num[ : mid ] # 분할
        right = num[ mid : ] # 분할 
        left = merge_sort(left) # 재귀적용
        right = merge_sort(right) # 재귀적용 
        return merge(left, right) # 병합 알고리즘 적용
    
def merge(left, right):
    result = []
    # left와 right의 시작 포인트
    i = 0
    j = 0 
    while i < len(left) and j < len(right):
        # 두 포인터가 가리키는 요소를 비교하고 더 작은 요소를 result 배열에 추가
        # 이후 더 작은 요소를 포함하는 하위 배열의 포인터를 다음 인덱스로 이동
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    # 하위 배열 중 하나가 완전히 처리된 후 다른 하위 배열의 나머지 요소를 result 배열에 추가
    # while 루프가 완료된 후 하위 배열 중 아직 result에 추가되지 않은 일부요소가 남아있을 수 있음
    # 그렇기 때문에 두 하위 배열의 모든 요소가 result 배열에 추가해야 됨
    result += left[i : ]
    result += right[j : ]
    return result

print(merge_sort(num))