손실함수

AI Scientist를 목표로!·2022년 12월 1일

1. 손실함수의 개념

지도학습(Supervised Learning) 시 예측한 값(pred)과 실제 값(label)의 차이를 비 교하기 위한 함수
즉, 함수 중에 알고리즘이 얼마나 잘못 예측하는 정도
목적 함수(Objective Function), 비용 함수(Cost Function), 에너지 함수(Energy Function) 등 다양하게 불림
손실이 커질 수록 모델 학습이 잘 안되고 있다고 해석이 가능하며,
반대로 손실이 작아질 수록 모델 학습이 잘 되고 있다고 해석 가능

2. 손실함수를 쓰는 이유

신경망 학습에는 최적의 매개변수(가중치와 편향)값을 탐색할 때, 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾는다.
이 때, 매개변수의 미분을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서리 갱신하는 과정을 반복한다.
한 가중치 매개변수의 손실 함수의 미분 = 가중치 매개변수의 값을 아주 조금 변화시켰을 때, 손실 함수가 어떻게 변하는가??
- 만일 미분의 값이 음수(-)일 경우, 가중치 매개변수를 양(+)의 방향으로 변화시켜 손실함수의 값을 줄인다.
- 미분의 값이 양수(+)일 경우, 가중치 매겨변수의를 음(-)의 방향으로 변화시켜 손실함수의 값을 줄인다.

3. 손실 함수의 종류

3-1. 평균제곱오차(Mean Squared Error, MSE)

MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2

$y$ : 신경망의 출력(각 뉴런의 output)

$\hat{y}$ : 정답 레이블

$i$ : 데이터 차원의 수

관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 수하는 분산과 유사한 개념
오차제곱합(SSE) 대신 평균제곱오차(MSE)를 사용하는 이유
- 단순히 실제 데이터와 예측 데이터 편차의 제곱 합이었던 오차제곱합(SSE)을 평균으로 만든 것
- 오차제곱합(SSE)의 값은 항상 양수이며, 데이터가 많아질 수록 값은 기하급수적으로 증가한다.
- 이로인해, 오차제곱합(SSE)으로는 실제 오차가 커서 값이 커지는 것인지 아니면 데이터의 양이 많아서 값이 커지는 것인지 구분할 수 없게된다.
평균제곱오차(MSE)는 언제 사용하는가?
- 회귀분석에서 모델의 적합도를 판단하는 결정계수 $R^2$ 의 분자로 사용
- 즉, 회귀분석이 연속형 데이터를 사용해 관계를 추정하듯 평균제곱오차(MSE)역시 주식 가격 예측과 같은 연속형 데이터를 사용할 때 사용된다.
구현
- 파이토치 MSE 공식 사이트

  import numpy as np

def MSE(real, pred):
    return (1/len(real)) * np.sum((real - pred)**2)

def SSE(real, pred):
     return 0.5 * np.sum((real - pred)**2)
     
--------------------------------------
Data가 100개일 때, SSE의 결과: 0.14375
Data가 1000개일 때, SSE의 결과: 12.51875
--------------------------------------
Data가 100개일 때, MSE의 결과: 0.00288
Data가 1000개일 때, MSE의 결과: 0.0025     
--------------------------------------

3-2. 평균제곱근오차(Root Mean Squared Error, RMSE)

RMSE = \sqrt{\frac{1}{n}\sum_{k}^{n}(y_k - \hat{y_k})^2}

평균제곱오차(MSE)는 분산과 비슷하며, 마찬가지로 편차 제곱 합을 하였기 때문에 실제 편차라고 보기 힘들어, 분산과 표준편차 처럼 제곱근(Root)를 씌운 것이 평균제곱근오차(RMSE)
분산대신 표준편차를 사용하는 것과 비슷하게 평균제곱오차(MSE)는 실제 편차를 반영한다고 볼 수 없다.
평균제곱오차(MSE)의 "큰 오류를 작은 오류에 비해 확대 시킨다"는 것을 제곱근(Root)해줌으로 써 보정이 들어갔다.
즉, 평균제곱근오차(RMSE)는 제곱근(Root)을 사용함으로서 왜곡을 줄여주기 때문에 오차를 보다 실제 편차와 유사하게 볼 수 있다.

구현

파이토치

  class RMSELoss(torch.nn.Module):
    def __init__(self):
        super(RMSELoss,self).__init__()

    def forward(self,x,y):
        eps = 1e-6  # 역전파에서 NaN이 발생하는 것을 방지하기 위해 앱실론 추가
        criterion = nn.MSELoss()
        loss = torch.sqrt(criterion(x, y) + eps)
        return loss

    def RMSE(real, pred):
       return np.sqrt((1/len(real)) * np.sum((real - pred)**2))

3-3. 교차 엔트로피 오차(Cross Entropy Error, CEE)

범주형 데이터를 분류할 때 주로 사용

Entropy란 무엇인가?

H(P) = -\sum_{x}P(x)log(P(x))

$c$ : 범주의 개수
$q$ : 사건의 확률 질량 함수

불확실성에 대한 척도
만일 가방안에 빨간공 만 들어 있을 경우, 무엇을 뽑아도 빨간 공이기 때문에 Entropy는 0 즉, 불확실성은 없다
반대로, 빨간공 반 파란공 반이 있을 경우, 뽑았을 때 어떤색의 공이 나올지 알 수 없다. 즉, 불확실성이 크다

예시1) 가방안에 빨간공 20개 / 파란공 80개 들어있는 경우

$H(q)=-(0.2log(0.2) + 0.8(log(0.8)) = 0.5$

예시2) 가방안에 빨간공 1개 / 파란공 99개 들어있는 경우

$H(q)=-(0.99log(0.99) + 0.01(log(0.01)) = 0.08$

즉, Entropy는 예측하기 쉬운 일보다는 예측하기 어려운 일에서 값이 더 높다

Cross-Entropy

H(P, Q) = -\sum_{x}P(x)logQ(x)

실제 분포 Q를 모를때, 모델링을 통해 구한 분포인 P를 통해 Q를 예측하는 것
Q와 P가 모두 들어가서 Cross-Entropy라고 부름

Kullback-Leibler Divergence

인공지능 모델을 잘 학습한다는 것은 정답의 분포를 모델이 잘 따라하도록 하는 것
즉, 정답 분포와 모델이 예측한 값의 분포가 비슷해지도록 만다는 것
KL-Divergence는 정단 분포와 모델의 예측값의 분포가 얼마나 비슷한지를 측정할 때 사용 되는 지표

D_{KL}(P||Q) = \sum_{x}P(x)log\frac{P(x)}{Q(x)}

보통 "가짜 분포 Q가 진짜 분포 P를 얼마나 잘 따라왔는가"로 해석

수식을 다르게 정리하면

= \sum_{x}P(x)log{P(x)} - \sum_{x}P(x)log{Q(x)}

= -H(P) + CE(P,Q)

로 위에서 설명한 (Entropy + Cross-Entropy)의 값으로 나뉜다.
P가 정답 분포이고, 분류 문제의 경우 정답은 하나의 1의 값을 가지고 나머지는 0
의 값을 가지는 One-Hot 형태이다

따라서 이값을 Entropy 수식에 넣으면 0이 된다.

즉, 분류 문제에서 KL-Divergence는 $D_{KL}(P||Q) = CE(P,Q)$ 가 된다.

그로인해 Cross-Entropy의 값을 최적화 하는 것이 모델이 정ㄷ바 분포를 잘 따라가도록 하는 셈이 된다.

Cross-Entropy Loss Function

개,고양이,사자에 대한 다중 분류 문제
- 개 / 고양이 / 사자에 대한 예측값 = [0.2,0.3,0.5]
- 실제 정답값 = [0,0,1]
Cross-Entropy의 값은 $-1log(0.5)$ 의 값이 된다.
즉, 정답 레이블에서 정답에 해당하는 위치의 확률의 로그 값이 출력된다.

예측값이 단일 항목으로 이루어져있다면 (ex, [0.5])

단순 이진 분류이므로, Binary Cross Entropy 를 사용

예측값이 다중 항목으로 이루어져있으며, 각 항목의 확률 합이 1이상일 경우 (ex, [0.7, 0.6, 0.4])

멀티 이진 분류이므로, Binary Cross Entropy 를 사용

예측값이 다중 항목으로 이루어져있으며, 각 항목의 확률 합이 1 이라면 (ex, [0.5, 0.2, 0.3])

다중 분류이므로, Cross Entropy 를 사용

구현
- 파이토치 CELoss 공식 사이트
- PyTorch에서는 softmax와 cross-entropy를 합쳐놓은 것 을 제공하기 때문에 맨 마지막 layer가 softmax일 필요가 없다.
- ```
def CEE(predict, label):
    delta = 1e-7
    return -np.sum(label * np.log(predict + delta))
```

3-4. 이진 교차 엔트로피 오차 (Binary Cross Entropy Error, BCEE)

Loss = -\frac{1}{N}\sum_{i=1}^{N}(y_i*log(\hat{y_i}) + (1-y_i)*log(1-\hat{y_i}))

도출 과정
- 이진 분류이기 때문에 y= 0과1만 존재 $H(y)= -\sum_{i=1}^{N}(y_i*log(\hat{y_i}))$ $H(y-1)= -\sum_{i=1}^{N}((1-y_i)*log(1-\hat{y_i}))$ $H(y) + H(y-1)= -\sum_{i=1}^{N}(y_i*log(\hat{y_i}) + (1-y_i)*log(1-\hat{y_i}))$ $Loss = -\frac{1}{N}\sum_{i=1}^{N}(y_i*ln\hat{y_i} + (1-y_i)*ln(1-\hat{y_i}))$
나누고자 하는 분류의 개수에 따라 사용하는 손실함수가 변경됨
범주가 2개인 데이터는 Sigmoid(0 ~ 1) 또는 tanh(-1 ~ 1) 활성화 함수를 사용해 값을 반환
로그 손실(Log Loss) 또는 로지스틱 손실(Logistic Loss)라 불리며, 즈로 로지스특 회귀의 손실함수로 사용된다.

구현

파이토치 BCELoss 공식 사이트

def BCEE(predict, label):
     delta = 1e-7
     pred_diff = 1 - predict
     label_diff = 1 - label
     result = -(np.sum(label*np.log(predict+delta)+label_diff*np.log(pred_diff+delta)))/len(label)

     return result

BCEWithLogitsLoss

BCELoss 앞에 Sigmoid layer 를 더한 것입니다. (Sigmoid + BCELoss) 따라서 따로 sigmoid 나 softmax를 해줄 필요가 없다.

torch.nn.BCEWithLogitsLoss(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)

3-5. 범주형 교차 엔트로피 오차(Categorical Cross Entropy Error, CCEE)

Loss = -\frac{1}{N}\sum_{j=1}^{N}\sum_{i=1}^{C}t_{ij}log(y_{ij})

Class가 3개 이상인 데이터를 대상으로 사용하는 손실함수
주로 Softmax 활성화 함수가 사용
실제 라벨은 One-Hot Vector로 구성
출력된 Vector는 각 Class에 속할 확률로 나오며, 총합은 1
Cross-Entropy Error를 N개의 데이터셋에 대해 1개의 스칼라를 추출하는 방법

구현

  def CCEE(predict, label):
     delta = 1e-7
     log_pred = np.log(predict + delta)

     return -(np.sum(np.sum(label * log_pred, axis = 1)))/label.shape[0]

3-6 음의 로그 가능도 손실(Negative Log Likelihood Loss, NLL)

L(y) = -log(y)

분류 문제에서 사용
가중치(Weight)는 Class 불균형 문제를 개선하기 위해 수동으로 가중치별 학습 비중의 스케일을 조정하기 위해 사용
- 예를 들어, Class의 개수가 3개이고, Class별 데이터의 개수가 (10,50,100)라면, 가중치는 데이터 개수와 역의 관계로 대입을 해주게 됨
- 핵심은 적은 개수의 데이터에 해당하는 클래스에 높은 가중치를 주어 학습 양을 늘림
log 함수와 음(-)의 부호를 사용해 Softmax 출력값이 낮은 값은 $-log(y)$ 값이 크도록 만들 수 있고, Softmax 출력값이 높은 값은 $-log(y)$ 의 값이 0에 가깝도록 만든다.
다시말하면, 정답 클래스의 Softmax 출력이 높다면 출력이 정확한 것이므로 $-log(y)$ 의 값이 매우 작아지게 되고, 반대의 경우에는 큰 값을 가지게 된다.

3-7 Focal Loss

FL(p_t) = -α_t(1-p_t)^γlog(p_t)

등장 배경

one-stage Network(YOLO,SSD등)의 Dense object Detection은 Two-Stage Network(R-CNN)에 비해 속도는 빠르지만 성능은 낮다
- Dectector는 한장에 이미지에서 $10^4 - 10^5$ 개의 후보 위치를 제안하지만 실제로는 몇개의 Object만 존재
- 분류하기 쉬운 easy negative 들이 대부분인데 이들이 학습에 기여하는 것이 없어 학습에 비효율적인 문제 발생
- 수많은 EASy negative들이 학습 과정을 압도하므로 비일반적인 모델이 학습되는 문제 발생
극단적인 Class간 Unbalance에 때문
Obh
즉, Focal Loss는 One-stage object detection에서 object와 background의 클래스 간 Unbalance가 극도로 심한 상황(1대 1000)을 해결하기 위해 제안

작동원리

Easy Example의 weight를 줄이고 Hard Negative Example에 대한 학습에 초점을 맞추는 Cross Entropy Loss 함수의 확장판

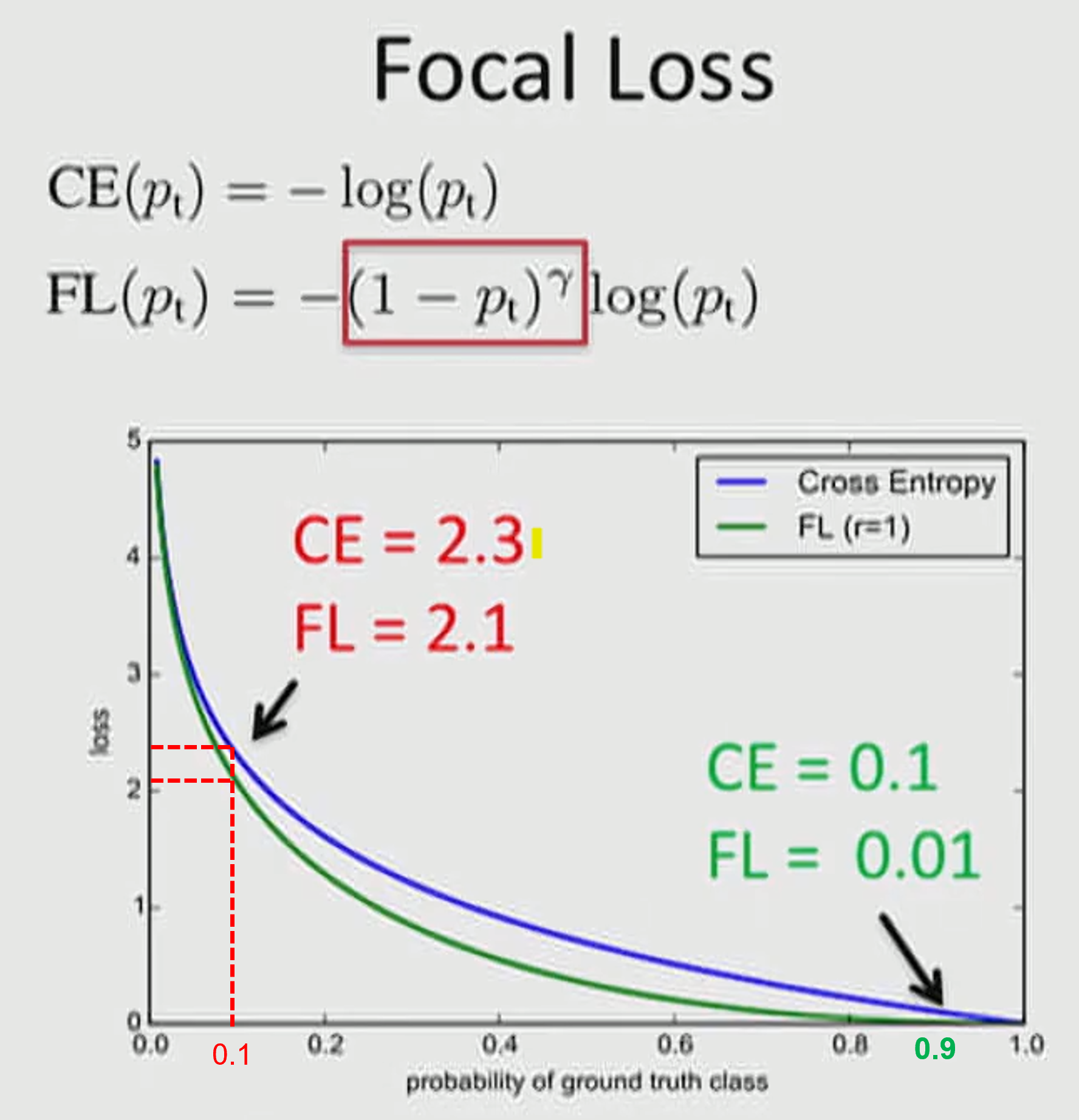
빨간색 = Hard Case 문제
초록색 = Easy Case 문제
(그래프에는 α=1,γ=1적용)

$p+t$ = 0.1 인 경우
- $CE(0.1) = - log(0.1) = 2.30259$
- $FL(0.1) = - (1-0.1)log(0.1) = 2.07233$
$p+t$ = 0.9 인 경우
- $CE(0.9) = - log(0.9) = 0.1053$
- $FL(0.9) = - (1-0.9)log(0.9) = 0.01053$