Tree
트리는 그래프의 한종류로 그중에서도
DAG(Directed Acyclic Graph,방향성이 있는 비순환 그래프)의 한 종류다
부모 자식 관계를 가지는 자료구조로
계층이 있고 그룹(같은 레벨)이 있는 계층 모델이다
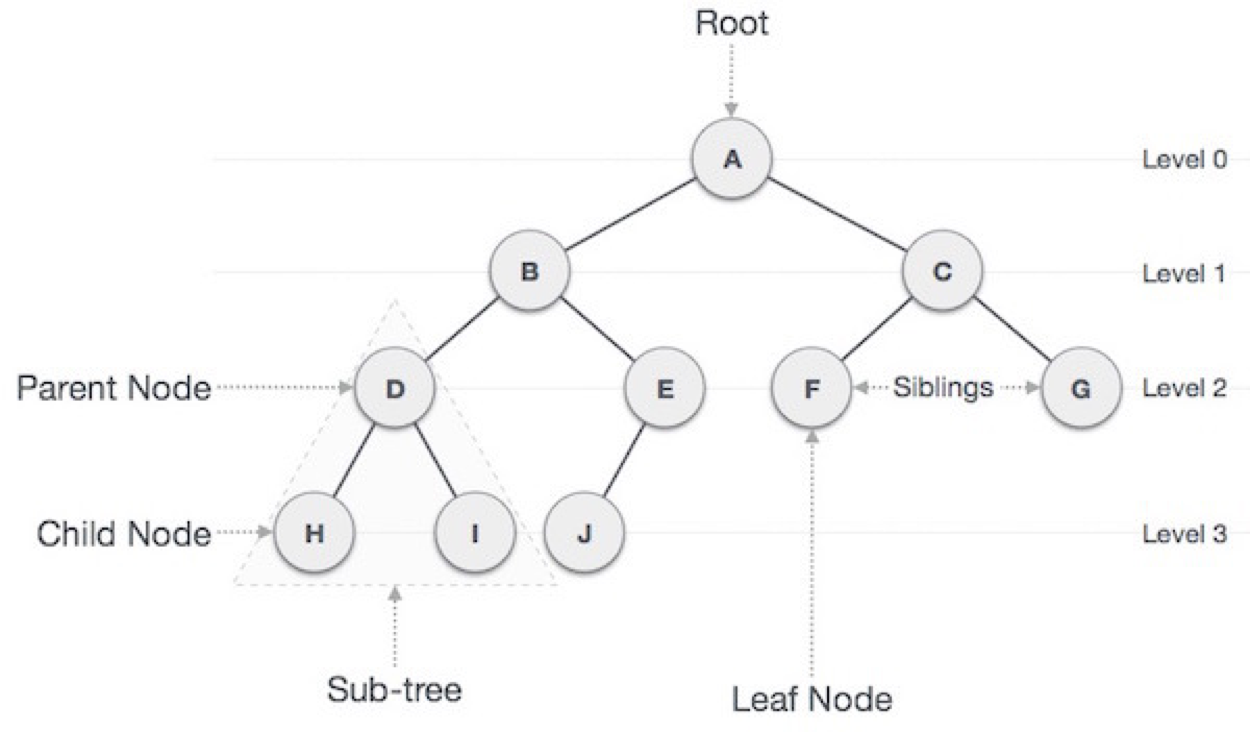
Tree 용어
Root node : 부모가 없는 노드. 트리는 루트 노드를 하나만 가진다.
Leaf node : 자식이 없는 노드.
Internal node : 리프 노드가 아닌 노드. 내부 노드 라고도 한다.
Edge : 노드를 연결하는 선. link,branch 라고도 한다.
Siblings : 같은 부모를 가지는 노드
Size : 자신을 포함한 모든 자식 노드의 갯수
Level : 트리의 특정 깊이를 가지는 노드의 집합.
Depth : 트리의 어떤 노드에 도달하기 위해 거쳐야 하는 간선(Edge)의 수
Height : 루트 노드에서 가장 깊숙히 있는 노드의 깊이(Depth)
binary tree
차일드 노드가 최대 2개 까지만 붙는 트리를 Binary Tree(이진트리)라고 한다 .
3개가 붙으면 ternary Tree 라고 한다.
binary search tree
이진트리는 다른 조건없이 차일드가 최대 2개까지만 붙을 수 있다.
바이너리 서치트리는 현재노드 왼쪽 노드와 그 이하 차일드 노드들의 값은
현재 노드의 값보다 작아야 하고
오른쪽 노드와 이하 차일드 노드들의 값은 현재 노드의 값보다 커야 한다.
그렇기 때문에 해당 노드보다 큰 값을 찾고 싶으면 오른쪽 차일드 노드로 가고,
작은 값을 찾고 싶으면 왼쪽 차일드 노드로 가면 쉽게 찾을 수 있다
Balance
왼쪽 오른쪽 노드의 갯수가 정확하게 맞아야 하는건 아니고
노드들이 왼쪽,오른쪽 어느 한쪽으로 지나치게 치우치지 않으면 밸런스가 맞는다고 한다 .
Binary Tree Traversal
binary tree 의 모든 데이터 순회하는 방법은
Inorder, Preoredr, postorder 3가지가 있다 .
Inorder
1.left
2.root
3.right
Preorder
1.root
2.left
3.right
Postorder
1.left
2.right
3.root
graph

단순히 노드(node)와 노드를 잇는 간선(edge)들을 모아둔 자료 구조
graph 관련 용어
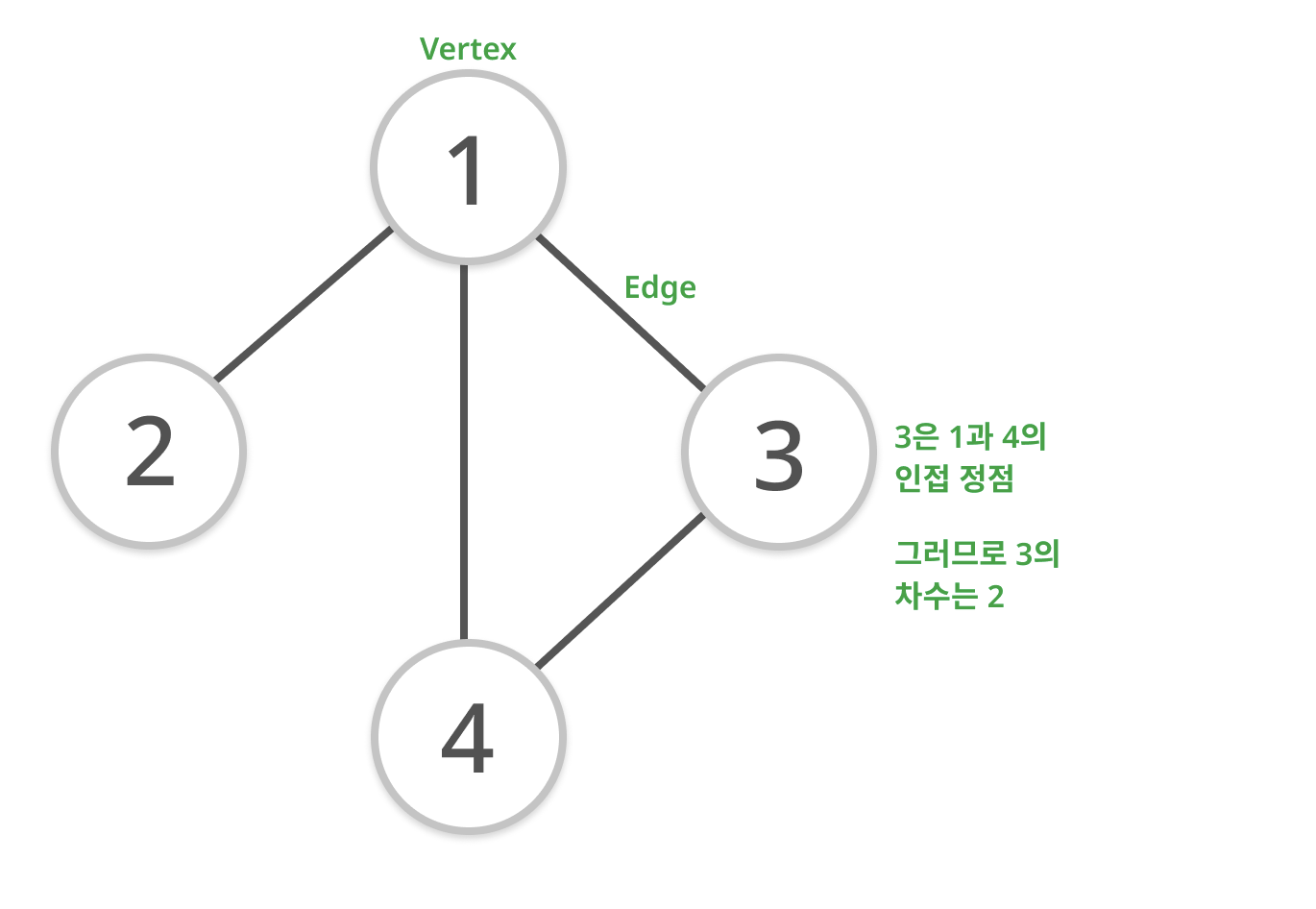
Vertex(정점) : 위치라는 개념. node라고도 부름
Edge(간선) : 위치간의 관계,즉 노드를 연결하는 선
Adjacency Vertex(인접 정점) : 간선에 의해 직접 연결된 정점
Degree(차수) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
graph의 구현 방법
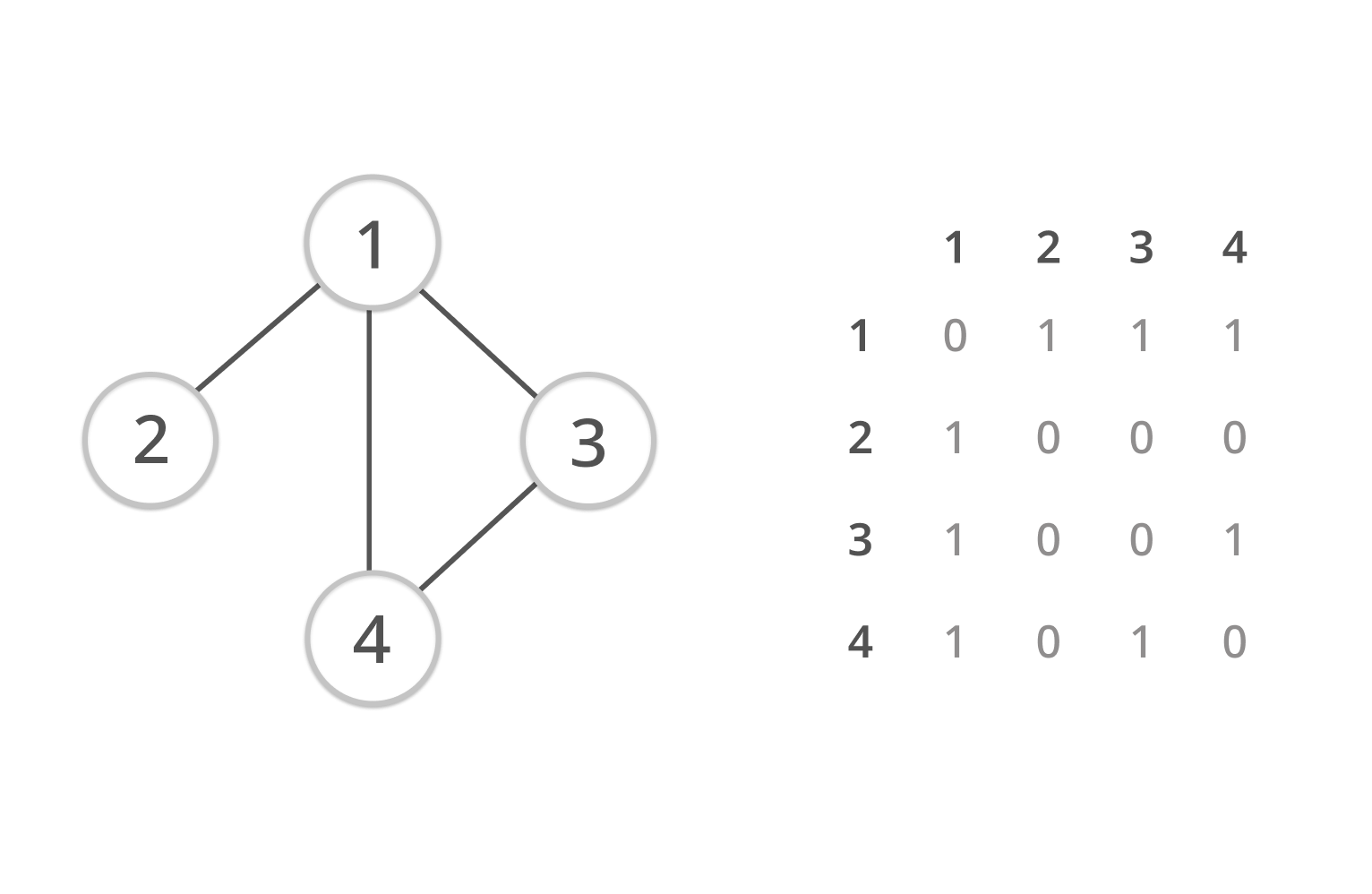
Adjacency Matrix (인접 행렬)
인접 행렬은 정점간의 연결관계를 이차원 배열로 나타내는 방식.
인접행렬을 ad[x][y]라고한다면 다음과 같이 정의 할수 있다.
ad[x][y] : 정점 x에서 y로 가는 간선이 있으면 1 없으면 0
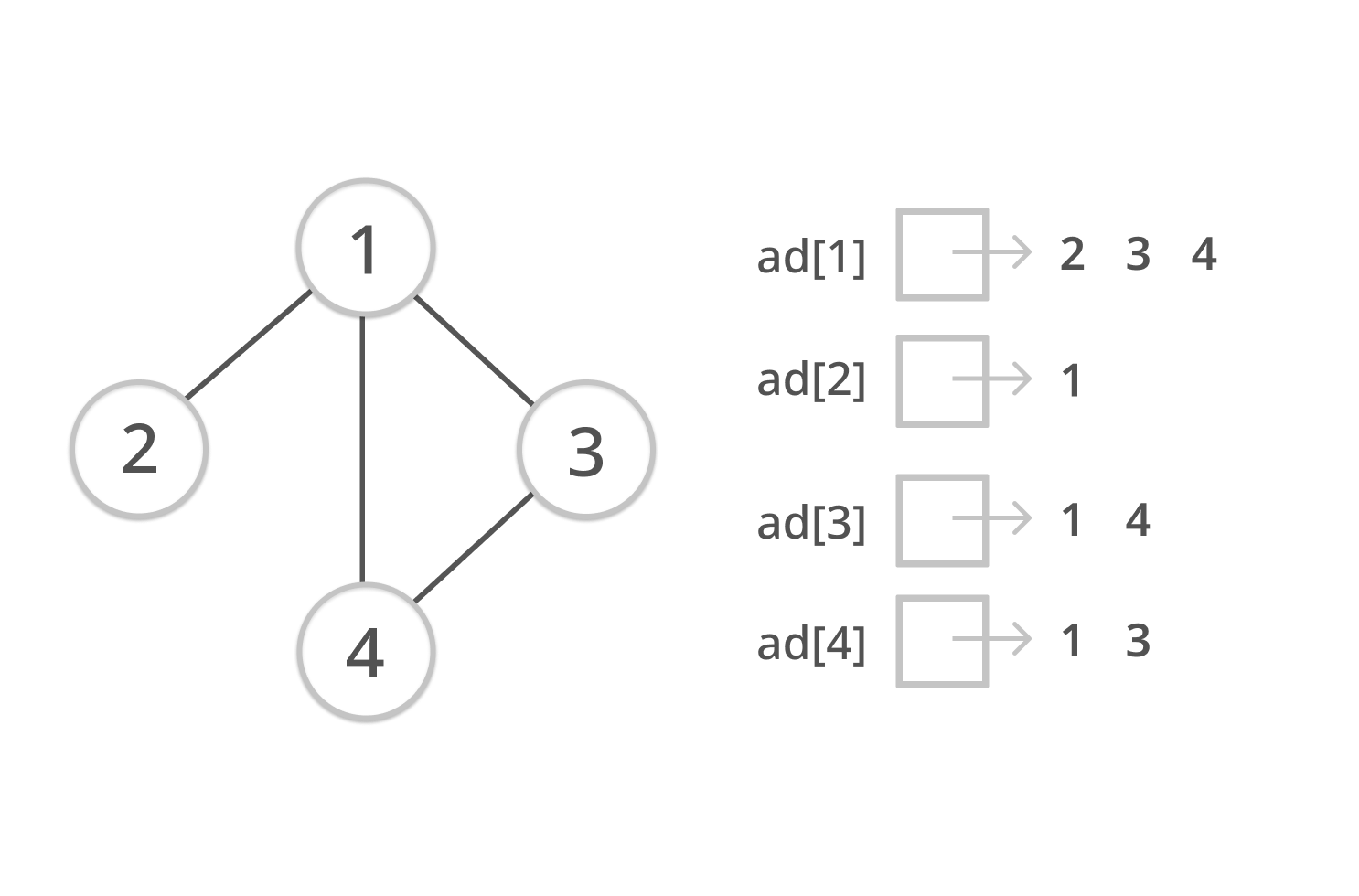
Adjacency List (인접 리스트)
모든 정점(혹은 노드)들을 인접 리스트에 저장한다.
즉, 각각의 정점에 인접한 정점들을 리스트로 표시한 것이다.
인접 리스트를 ad[x]라고 한다면 다음과 같이 정의 할 수 있다.
ad[x] : 정점 x에 연결된 모든 정점들을 원소로 갖는 리스트.
graph의 탐색 방법
DFS(Depth-first Search)
루트 노드(혹은 임의의 다른 노드)에서 시작해서 다음 분기로 넘어가기전에
해당 분기를 완벽하게 탐색하는 방법
즉, 넓게 탐색하기전에 깊게 탐색하는 것이다.
사용하는 경우: 모든 노드를 방문하고 싶을때 이 방법을 사용한다.
BFS(Breadth-first Search)
루트 노드(혹은 임의의 다른 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
즉.깊게 탐색하기 전에 넓게 탐색하는 것이다.
사용하는 경우:두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을때 사용하는 방법