시간 복잡도는 알고리즘에서 흔하게 활용되는 개념이다 .

알고리즘이란 ?

어떤 목적을 달성하거나 결과물을 만들어내기위해 거쳐야 하는 일련의 과정을 의미
라면을 끓이는 과정을 알고리즘으로 표현하자면

function cookingRamen(라면,계란){
  1.냄비에 물을 넣는다.
  2.물 넣은 냄비를 끓인다.
  3.if 물이 끓으면 라면 봉지안의 {면, 스프, 건더기}를 넣는다.
  4.if 계란 === true 라면 계란을 넣고 끓인다.
  5.면이 익으면 불을 끈다 
  6.완성된 라면을 냄비 밖으로 옮긴다.
};
 cookingRamen(진라면, true) ==> 맛있따.

알고리즘은 각각 각기 다른 모양과 형태를 지니고 있기 때문에
시간 복잡도를 설명하는데 자주 사용된다. 애플 파이를 자르는데 100가지 방법이 있는 것처럼
같은 문제도 여러가지 알고리즘으로 풀 수 있다.

시간복잡도를 분석하는 것은 input n에 대하여 알고리즘이 문제를 해결하는데 얼마나 오랜 시간이 걸리는 지를 분석하는 것과 같다. 그리고 이는 Big-O표기를 이용하여 정의할 수 있다.

Big-O 표기

시간 복잡도의 가장 간단한 정의는 알고리즘의 성능을 설명하는 것이다.
다른 의미로는 알고리즘을 수행하기 위해 프로세스가 수행해야 하는 연산을 수치화 한 것
왜 실행 시간이 아닌 연산 수치로 판별할까? 명령어의 실행시간은
컴퓨터의 하드 웨어, 혹은 프로그래밍 언어에 따라 편차가 크게 달라지기 때문에
명령어의 실행 횟수 만을 고려한다.

시간 복잡도에서 가장 중요하게 큰 영향을 미치는 것은 n의 단위이다.

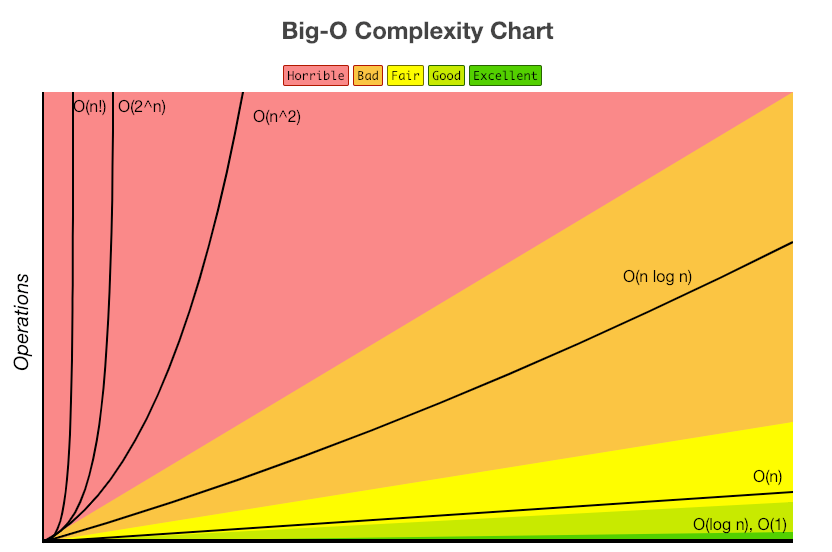
대표적인 시간 복잡도들을 간단하게 정의해보자
1.O(1) 상수 시간 : 입력값 n이 주어졌을 때, 알골즘이 문제를 해결하는데
오직 한 단계만 거친다.

2.O(log n) 로그 시간: 입력값 n이 주어졌을 때, 문제를 해결하는데 필요한 단계들이
연산마다 특정 요인에 의해 줄어든다.

3.O(n) 선형 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계이다

4.O(n^2) 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱이다.

5.O(C^n) 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C의 n 제곱이다.

위의 정의를 가지고 아래 예제를 계산한다.

let n = 16 // 입력값 n 이 16일때

O(1) = 1step // O(1)은 시간복잡도가 1
O(log n) = 4step //O(log n)는 시간복잡도가 4
O(n) = 16step //O(n)은 시간복잡도가 16
O(n^2) = 256step //O(n^2)은 시간복잡도가 256
O(2^16) = 65,636step //O(C^n)은 시간복잡도가 65,536

O(1) 상수 시간

아래 예제 처럼 입력에 관계 없이 복잡도는 1이다.

function helloWorld(){
  console.log('hello world')
};

O(log n) 로그 시간

주로 입력 크기에 따라 처리 시간이 증가하는 정렬 알고리즘에서 많이 사용
다음은 이진 탐색 트리의 예

const BinarySearch = function(target){
      if(this.value === target){
          return true
      }
      if(this.value < target){
          if(this.right !== null){
            return this.right.contains(target)
          }         
      }else {
          if(this.left !== null){
            return this.left.contains(target)
          }
      }
      return false;
    }

O(n) 선형 시간

입력이 증가하면 처리 시간 또는 메모리 사용이 선형적으로 증가한다.

function loop(n){
  for(let i = 0; i < n; i++){
    console.log(i);
  }
}

O(n^2) 2차 시간

반복문안에 반복문. 반복문이 두번 있는 케이스

function loopSquare(n){
  for(let i = 0; i < n; i++){
    for(let j = 0; j < n; j++){
      console.log(i, j)
    }
  }
};

시간복잡도를 구하는 요령

아래의 예를 통해 각 문제의 시간 복잡도 유형을 빨리 파악할 수 있다.

• 하나의 루프를 사용하여 단일 요소 집합을 반복 하는 경우 : O(n)
• 컬렉션의 절반 이상을 반복 하는 경우: O(n / 2) -> O(n)
• 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복 할 경우 : O(n + m ) -> O(n)
• 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O(n^2)
• 두 개의 중첩 루프를 사용하여 다른 콜렉션을 반복할 경우 : O(n * m) -> O(n^2)
• 컬렉션 정렬을 사용하는 경우 : O(n * log(n))