[Algorithm] 위상 정렬(Topology Sort) C++

 위상 정렬은 방향성 비순환 그래프(DAG)에서 노드의 순서를 정하는 알고리즘이다. 작업 순서를 정해야 할 때 사용할 수 있다. 다시 말하자면, 순서를 지켜야하는 작업을 차례로 수행해야할 때 작업의 순서를 결정해주는 알고리즘이다. 답이 여러가지 존재할 수 있다는 점을 유의해야한다.

방향성 비순환 그래프 DAG(Directed Acycle Graph)

DAG(Directed Acycle Graph)란 사이클이 없는 방향그래프이다.

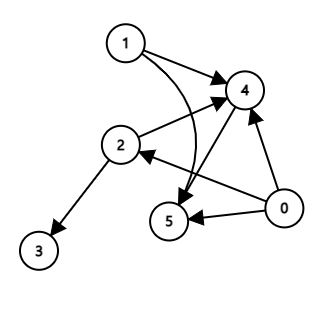
 각 노드와 간선을 한번씩 순회하면서 정렬을 수행하는 방식으로 동작한다. Incoming이 없는 노드를 계속해서 찾아야하는데 cycle이 존재하는 그래프에서는 Incoming이 존재하는 노드를 찾지 못하는 순간이 오기 때문에, 위상 정렬에서는 반드시 사이클이 존재하지 않는 그래프에서 사용해야한다.

위상 정렬 로직

1. 진입 차수 배열 생성

2. 진입 차수가 0인 노드 큐에 삽입

3. 큐에서 노드 꺼내기:
큐에서 노드를 하나 꺼내고, 해당 노드를 결과 리스트에 추가한다. 그 노드와 연결된 모든 간선을 제거하고, 간선이 제거된 노드들의 진입 차수를 감소시킨다. 이후 2번을 실행한다.

4. 큐가 빌 때까지 반복

5. 결과 확인:
결과 리스트의 길이가 그래프의 노드 수와 같다면 위상 정렬이 완료된 것이다. 그렇지 않다면 사이클이 존재하여 위상 정렬이 불가능한 상태임을 알 수 있다.

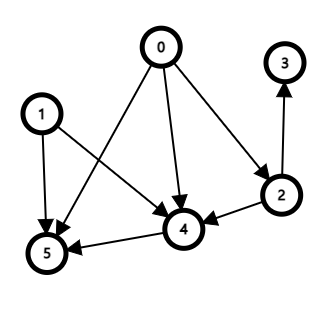
위의 그래프로 위상정렬을 진행해 보자.

먼저 진입 차수 배열을 만든다.

정점	0	1	2	3	4	5
진입 차수	0	0	1	1	3	3

진입 차수가 0인 노드 0, 1을 큐에 넣는다.

큐	0	1
답

---

큐에서 노드 0을 꺼내고 결과 리스트에 추가한다. 꺼낸 노드와 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다.

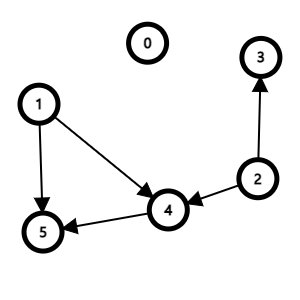
큐	1
답	0

정점	0	1	2	3	4	5
진입 차수	0	0	0	1	2	2

---

이후 진입 차수가 0인 노드 2를 큐에 집어넣는다

큐	1	2
답	0

큐에서 노드1 을 꺼내 결과 리스트에 갱신하고 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다.

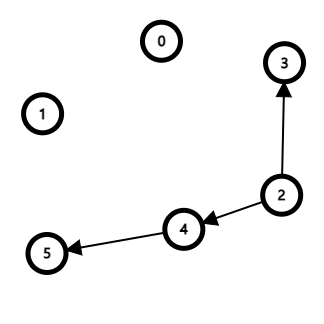
큐	2
답	0	1

정점	0	1	2	3	4	5
진입 차수	0	0	0	1	1	1

---

진입 차수가 0인 노드가 없으므로 건너뛴다.

큐	2
답	0	1

큐에서 노드 2를 꺼내 결과 리스트에 갱신하고 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다.

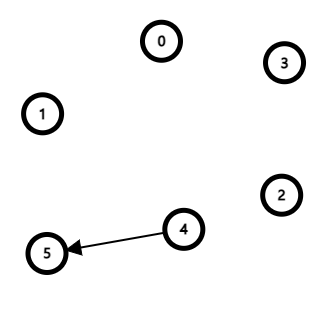
큐
답	0	1	2

정점	0	1	2	3	4	5
진입 차수	0	0	0	0	0	1

---

진입 차수가 0인 노드 3, 4를 큐에 넣는다.

큐	3	4
답	0	1	2

큐에서 노드 3을 꺼내 결과 리스트에 갱신하고 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다. 노드 3은 말단 노드이므로 제거되는 간선이 존재하지 않는다.

큐	4
답	0	1	2	3

정점	0	1	2	3	4	5
진입 차수	0	0	0	0	0	1

---

진입 차수가 0인 노드가 없으므로 건너 뛴다.

큐	4
답	0	1	2	3

큐에서 노드 4를 꺼내 결과 리스트에 갱신하고 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다.

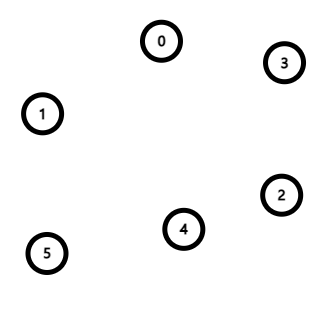
큐
답	0	1	2	3	4

정점	0	1	2	3	4	5
진입 차수	0	0	0	0	0	0

---

진입 차수가 0인 노드 5를 큐에 넣는다.

큐	5
답	0	1	2	3	4

큐에서 노드 5를 꺼내 결과 리스트에 갱신하고 연결된 모든 간선을 제거한다. 간선이 제거된 노드들의 진입 차수를 갱신한다. 노드 5는 말단 노드이므로 제거되는 간선이 존재하지 않는다.

큐
답	0	1	2	3	4	5

정점	0	1	2	3	4	5
진입 차수	0	0	0	0	0	0

 이렇게 위상 정렬을 완료했다. 완료한 결과는 공교롭게도 0->1->2->3->4->5가 나온 모습을 확인할 수 있다.

 시간복잡도는 O(V+E), 각 노드를 방문하고 연결된 간선을 지우고 갱신하는 작업으로 이루어져있기 때문이다. 앞서 설명한 이론을 바탕으로 구현한 C++ 코드를 확인해보자.

Source Code

#include <iostream>
#include <vector>
#include <queue>
#define Max 10

using namespace std;

int degree[Max];
vector<int> graph[Max];

void topologySort(int n) {
	int ans[Max];
	queue<int> q;

	//진입 차수가 0인 노드를 큐에 삽입한다.
	for (int i = 0; i < n; i++) 
		if (degree[i] == 0) q.push(i);

	for (int i = 0; i < n; i++) {
		int x = q.front();
		q.pop();
		ans[i] = x;
		//큐에 있는 값을 ans배열에 삽입하고 pop한다.
		for (int j = 0; j < graph[x].size(); j++) {
			int y = graph[x][j];
			degree[y]--;
			//갱신된 진입차수가 0이라면 큐에 삽입한다.
			if (degree[y] == 0) q.push(y);
		}
	}

	for (int i = 0; i < n; i++) 
		cout << ans[i] << ' ';
}

int main() {
	int x, y;
	int vertex, edge;

	cin >> vertex >> edge;
	for (int i = 0; i < edge; i++) {
		cin >> x >> y;
		graph[x].push_back(y);
        degree[y]++;
	}
	topologySort(vertex);

	return 0;
}